Лема 3.3

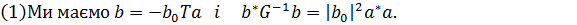
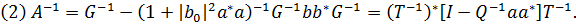
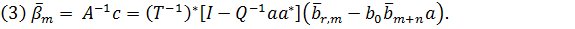
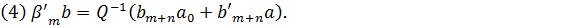
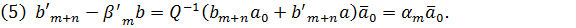
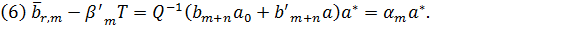
Доведення леми є простим, тому ми його опустимо.

Доведення теореми 3.1.

Виходячи з (3.3) ми вже вище довели (1). Використовуючи представлення в (3.2) і визначення 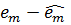ми маємо

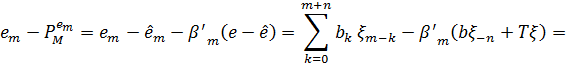
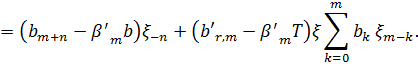
Твердження (2) слідує з леми (3.3)(5),(6). нарешті, ми отримуємо (3) з (2).

Доведення теореми 3.2.

Використовуючи теорему 3.1 (2) і останню тотожність в (2.1), ми отримаємо

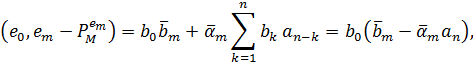
Звідси отримуємо (1). З (2.6) і (3.1),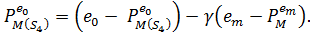

Тоді (2) випливає з теореми (3.1), і (3) виводиться застосуванням теореми (3.1)(2).

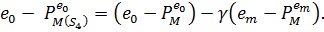
Ця тотожність необхідна для доведення (4). Так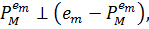

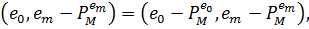
Котре, в силу (3.1) дає

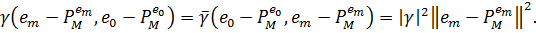
Таким чином

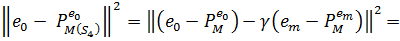
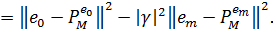
Тепер, 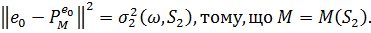З іншої сторони, з (1) ми маємо:

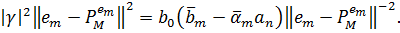
Таким чином, ми отримуємо (4), бажану формулу відстані (2.9).

Звичайно, це являє собою великий інтерес для обчислення 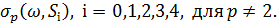Для і=0 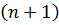– й крок проблема прогнозування була вирішена в [1], [10] з додатковою гіпотезою, що

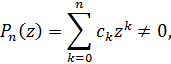
Для всіх 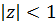, де коефіцієнти 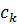визначаються наступним чином:

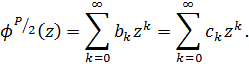
Використовуючи цей результат і співвідношення двоїстості (2.4), 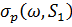знаходиться в [2]. Здається, цілком імовірно, що одномірний метод ортогоналізації який використовується в [2, теорема 5], може бути продовжений до 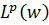, а потім за допомогою відношення двоїстості (2.4), можна також обчислити 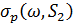. Вздовж цього розширення набору індексів може знадобитися припущення про місце нулів 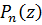впродовж кількох n, що піднімає питання про існування нетривіальних вагових функцій 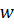, які задовольняють ці умови.

3 Основні результати

3.1 Перевірка гіпотези про двоїстість та ортогоналізацію.

Дата добавления: 2015-08-31