
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Уравнение Никольского
|
|
|
|
Уравнение изотермы адсорбции Фрейндлиха
Уравнение Фрейндлиха для адсорбции газа имеет вид:
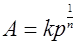 (11)
(11)
K и 1/n –постоянные уравнения Фрейндлиха.
Чаще всего это уравнение применяется в логарифмической форме:
 (12)
(12)
Уравнение в такой форме позволяет построить линейную зависимость lnA от lnp и графически определить оба постоянных параметра.
Логарифмическое уравнение Фрейндлиха для адсорбции из раствора имеет вид:
 (13)
(13)
Графически определяем постоянные параметры по линейной зависимости lnA от lnC. (рис.2)
Отрезок, отсекаемый на оси ординат равен lg k, а тангенс угла наклона прямой
равен 1/n.
 |
Рис.2. Изотерма адсорбции в координатах логарифмического уравнения.
При ионообменной адсорбции происходит стехиометрический обратимый обмен ионов между объемом раствора электролитов и адсорбентом.
Процессы ионного обмена на твердой поверхности характеризуются уравнением Б.П.Никольского:
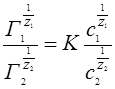 (14)
(14)
где 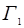 и
и  - количество ионов, поглощенных поверхностью сорбента (кмоль/кг),
- количество ионов, поглощенных поверхностью сорбента (кмоль/кг), 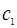 и
и 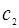 - равновесные концентрации ионов в растворе (кмоль/
- равновесные концентрации ионов в растворе (кмоль/ 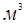 ), К – константа обмена, зависящая от способности ионов к адсорбции на данном сорбенте.
), К – константа обмена, зависящая от способности ионов к адсорбции на данном сорбенте.
Графически уравнение Б.П.Никольского изображается прямой, тангенс угла наклона которой и представляют величину константы К.
Примеры решения задач:
1. Рассчитать удельную поверхность адсорбента по изотерме адсорбции бензола на его поверхности. Площадь, занимаемая молекулой бензола, S0=49·10-20 м2.
| p P/PS | 0.024 | 0.08 | 0.14 | 0.20 | 0.27 | 0.35 | 0.46 |
| a·103, моль/кг | 14,9 | 34,8 | 47,2 | 56,8 | 66,3 | 79.3 | 101.0 |
Решение. Проверяют применимость к экспериментальным данным теории БЭТ. С этой целью рассчитывают абсциссу и ординату уравнения изотермы адсорбции БЭТ в линейной форме, т.е.
 и
и 
Результаты вычислений сводят в таблицу 1 и строят график зависимости y=f(x)
Таблица 1.
| p/ps | y, кг/моль | p/ps | y, кг/моль |
| 0,024 | 1,650 | 0,27 | 5,466 |
| 0,08 | 2,499 | 0,35 | 6,790 |
| 0,14 | 3,449 | 0,46 | 8,343 |
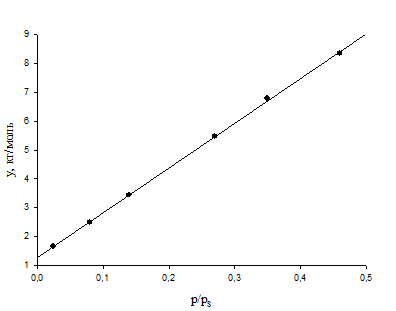
Рис.1 изотерма адсорбции в координатах линейной формы уравнения БЭТ.
Для определения адсорбционной емкости монослоя аm по графику зависимости у=f(x) находят константы уравнения прямой линии: отрезок, отсекаемый на оси ординат при p/ps=0, b0=1.24 кг/моль, и угловой коэффициент прямой b1=15.8 кг/моль. Для сравнения вычисляют b0 и b1
методом наименьших квадратов. Данные для расчёта b0 и b1 приведены в таблице 2.
Таблица 2.
| n | x | y, кг/моль | xy, кг/моль | x2 |
| 0,024 | 1,650 | 0,0396 | 5,76·10-4 | |
| 0,080 | 2,499 | 0,2000 | 6,4·10-3 | |
| 0,140 | 3,499 | 0,4830 | 1,96·10-2 | |
| 0,200 | 4,400 | 0,8800 | 4,00·10-2 | |
| 0,270 | 5,466 | 1,4550 | 7,08·10-2 | |
| 0,350 | 6,790 | 2,3765 | 0,123 | |
| 0,460 | 8,434 | 3,8778 | 0,212 |
k=13,65 и am=0,0489 моль/кг.
По величине аm рассчитывают удельную поверхность адсорбента:
S=S0amNA=49·10-20·0,0489·6,02·1023=14,4·103 м2/кг.
2. Вычислить предельный адсорбционный объём активированного угля БАУ по изотерме адсорбции бензола (таблица 3). Молярный объём бензола vm=89·10-6 м3/моль.
Таблица 3.
| p/ps | a, моль/кг | p/ps | a, моль/кг | p/ps | a, моль/кг |
| 1,33·10-6 | 0,50 | 1,63·10-2 | 2,25 | 0,327 | 2,86 |
| 2,13·10-5 | 0,85 | 3,77·10-2 | 2,39 | 0,460 | 3,00 |
| 1,21·10-4 | 1,18 | 9,47·10-2 | 2,56 | 0,657 | 3,19 |
| 5,60·10-4 | 1,55 | 0,201 | 2,74 | 0,847 | 4,47 |
Решение. Проверяют применимость уравнения (II.15) к экспериментальным данным. С этой целью вычисляют lg a и 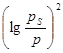 (таблица 4) и строят график зависимости
(таблица 4) и строят график зависимости  (Рис. II.2)
(Рис. II.2)
Таблица 4.
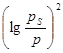
| lg a | 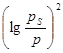
| lg a | 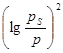
| lg a |
| 34,52 | -0,3010 | 3,19 | 0,3522 | 0,230 | 0,4564 |
| 21,82 | -0,0706 | 2,03 | 0,3784 | 0,113 | 0,4771 |
| 15,34 | 0,0719 | 1,05 | 0,4082 | 0,033 | 0,5038 |
| 10,58 | 0,1903 | 0,48 | 0,4378 | 0,005 | 0,6503 |
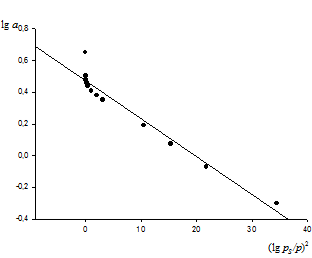
Рис.2 Изотерма адсорбции в координатах линейной формы уравнения М.М.Дубинина.
Как видно из рис.2, экспериментальные точки с хорошим приближением укладываются на прямую линию и, следовательно, уравнение (15) применимо к адсорбции бензола на активированном угле БАУ.
По отрезку, отсекаемому па оси lg a при 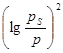 =0, находят
=0, находят 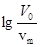 =0,435 и
=0,435 и
V0=0,239·10-3м3/кг.
3. По экспериментальным данным сорбции паров воды на активированном угле при Т = 293 К построить кривую капиллярной конденсации. Показать наличие гистерезиса и, используя ветвь десорбции, построить интегральную и дифференциальную кривые распределения пор по радиусам.
P/PS •••••••• 0,1 0,2 0,4 0,6 0,8 0,9 0,98
а адс ·103,моль/кг.... 3,75 5,3 6;2 8,75 10,4 12, 5 13,4
а дес·103, моль/кг.... 3,75 7,0 7,9 10,0 11,5 13,0 13,4
Vm =18·10 -3м3/моль, σ= 72,5-10-3 Дж/м2.'
Решение. Строят изотерму капиллярной конденсации в соответствии с условием задачи. Выбирают ряд точек на ветви десорбции (не менее шести—восьми), соответствующих определенным значениям p/pS, и рассчитывают объем пор, заполненных конденсатом, по уравнению V = aVm. Затем для этих же значений по уравнению

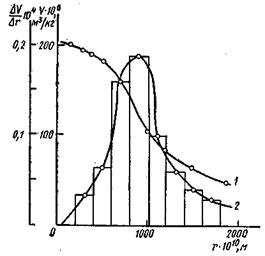
рассчитывают максимальный радиус пор, заполненных конденсатом при соответствующих давлениях p/ps. Полученные данные записывают в табл. 5 и строят структурную кривую адсорбента в координатах V=f(r). Из кривой находят ряд значений ΔV/Δr (табл.6) и строят дифференциальную кривую распределения объёма пор по радиусам в координатах ΔV/Δr=f(r)
Таблица.5 Данные для построения интегральной кривой распределения объёма пор по радиусам.
| № точки | P/PS | a дес·103,моль/кг | V·106,м3/кг | r·1010,м |
| 0,05 0,1 0,2 0,4 0,6 0,8 0,9 0,98 | 0,5 3,7 7,0 7,9 9,0 10,0 10,9 11,5 | 0,9 66,6 126,0 142,0 162,0 180,0 196,0 207,0 | 2,2 4,6 6,6 8,5 11,6 15,5 20,2 26,3 |
Таблица.6 Данные для построения дифференциальной кривой распределения объёма по радиусам.
| ΔV/Δr·10-4,м2/кг | Δ r ·1010,м | ΔV/Δr·10-4,м2/кг | Δ r ·1010,м | ΔV/Δr·10-4,м2/кг | Δ r ·1010,м |
| 1,5 0,5 |
Рис.3 Интегральная(1) и дифференциальная(2) кривые распределения.
|
|
|
|
|
Дата добавления: 2015-08-31; Просмотров: 6728; Нарушение авторских прав?; Мы поможем в написании вашей работы!