Уравнение Ламберта-Бера

Нефелометрия.

Интенсивность света, рассеянного некоторым объе­мом W коллоидного раствора, пропорциональна произведению ( c·W), т. е. общему числу рассеивающих частиц. На этой закономерности основан метод определения концен­трации, называемый нефелометрией. В соответствующем приборе—нефелометре имеются две кюветы переменного объема W₁ и W₂. В одну из них помещают раствор с из­вестной концентрацией c в другую—с неизвестной концентрацией с. Путем изменения величин W₁ и (или) W ₂ достигается вы­полнение равенства jr₁=jr₂,, т.о.:

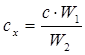(6)

Изменение интенсивности света, проходящего через любую среду, описывается законом Ламберта—Бера

I=-I₀ exp(-ξ·l) (7)

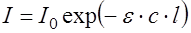(8)

где I —интенсивность прошедшего света, I₀ —интенсив­ность входящего в среду свет, l — толщина поглощающего слоя, ε -индивидуальная константа, зависящая от природы: вещества, длины световой волны и не зависящая от концентрации раствора.; с — концентрация вещества.

Обычно ε > 0, т. е, происходит ослабление проходя­щего света, но имеются особые среды, у которых ε< 0 т. е. происходит усиление света - это лазерные среды.

Примеры решения задач:

1. Алгоритм определения размеров частиц дисперсных систем не подчиняющихся уравнению Геллера.

1. Построить прямую в координатах IgD_λ - lgλ; тангенс угла наклона прямой равен коэффициенту α;

2. По данным ниже приведенной таблицы строят график в координатах Z – α, находят значение параметра Z, соответствующее ранее определенному α.

Таблица:1. Показатель степени α в уравнении Геллера в зависимости от параметра Z.

α.	Z	α	Z
3.812	2.0	3.090	5.0
3.686	2.5	2.807	5.5
3.573	3.0	2.657	6.0
3.436	3.5	2.533	6.5
3.284	4.0	2.457	7.0
3.121	4.5	2.379	7.5

3. По уравнению:

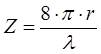
рассчитывают радиус частиц латекса. Сле­дует учесть, что при расчете r, нужно подставить среднее значение длин волн λср в том интервале, в котором опреде­лялся показатель степени α.. Величину λср находят по соотношению:

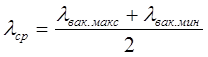
Найденное значение r соответствует среднему радиусу частиц латекса.

2. При исследовании гидрозоля золота методом точной ультрамикроскопии в объеме W = l,6·10^-11 подсчитано 70 частиц. Определить средний радиус частиц золя, приняв их форму за сферическую. Весовая концентр рация золя с = 7·10^-6 кг/м³, плотность γ= 19,3·10³ кг/м³.

Решение. Находим частичную концентрацию гидрозоля золота: ,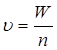

Где n – число частиц; W – объем.

.

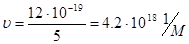Затем находим радиус: ,

.

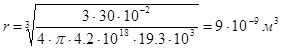3.Найти концентрацию исследуемого раствора NaCl и массу NaCl в исследуемом растворе, используя экспериментальные данные:

Концентрация раствора с мкг/мл 2.30 3.45 3.91 4.60 5.75

Интенсивность, I,% 28 42 47 55 67

Если интенсивность исследуемого раствора равна 32%, объем раствора равен 500 мл.

Решение

Построим график зависимости с мкг/мл от I,%.

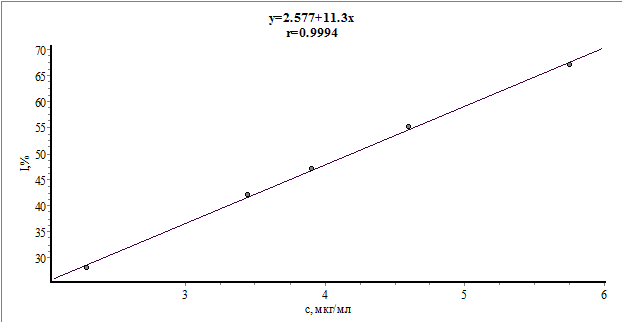
Интенсивности излучения NaCl, равной 32%, соответствует концентрация, равная 2.6 мкг/мл. Т.о. масса NaCl будет равна:

m = c·W,

(где с - концентрация раствора; W – объем)

m = 2.6·500 = 1300 мкг.

Дата добавления: 2015-08-31