Примеры решения задач. 1.Определите радиус частиц гидрозоля золота, если после установления диффузионно-седиментационного равновесия при 293 К на высоте Н = 8,56 см концентрация

1.Определите радиус частиц гидрозоля золота, если после установления диффузионно-седиментационного равновесия при 293 К на высоте Н = 8,56 см концентрация частиц изменяется в е раз. Плотность золота ρ = 19,3 г/см³, плотность воды ρ ₀ = 1,0 г/см³.

Решение. Распределение частиц по высоте при установлении диффузионно-седиментационного равновесия описывается гипсометрическим уравнением (5) Согласно условию задачи, n = n₀/e и ln n/n₀ = -1С учетом этого выражение для радиуса частиц принимает вид

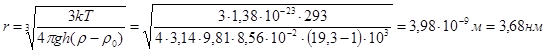
2.Частицы бентонита дисперсностью D = 0,8 мкм^-1 оседают в водной среде под действием силы тяжести. Определите время оседания τ₁ на расстояние h = 0,1 м, если плотность бентонита ρ = 2,1 г/см³, плотность среды ρ _о= 1,1 г/см³, вязкость среды η = 2·10^-3 Па·с. Во сколько раз быстрее осядут частицы на то же расстояние в центробежном поле, если начальное расстояние от оси вращения h₀ = 0,15 м, а скорость вращения центрифуги п = 600 об/с.

Решение. Из уравнения Стокса (9) выражаем

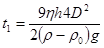, где

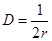
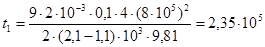с

Для частиц, оседающих в центробежном поле, справедливо соотношение

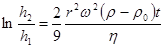
где h₂ = h₁ + h, ω =2πn - угловая скорость вращения центрифуги.

Время оседания в центробежном поле составит:

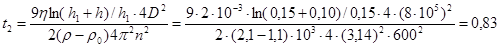с

Искомое соотношение равно

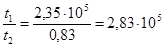
3 Какое центробежное ускорение должна иметь центрифуга, чтобы вызвать оседание частиц радиусом r = 5·10^-8 м и плотностью ρ = 3·10³кг/м³ в среде с плотностью ρ ₀=1·10³ кг/м³ и вязкостью η = 1·10^-3 Па·с при T = 300 К?

Решение. Для того чтобы происходило оседание частиц, необходимо преобладание скорости оседания над скоростью теплового движения примерно на порядок. Для оценки скорости теплового движения частиц рассчитывают средний сдвиг 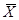за 1 с. По уравнению (2)

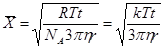
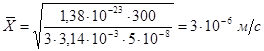
Задаются скоростью оседания u_ц = 3·10^-5 м/с и находится центробежное ускорение

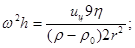
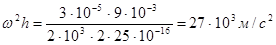
или

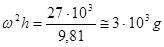
4.Расчитать и построить интегральную и дифференциальную кривые распределения частиц пека в воде. В результате графической обработки седиментационной кривой получены данные, помещенные в табл 5.1; плотность песка ρ = 2,1·10³ кг/м³; плотность воды ρ₀ = 1·10³ кг/м³; высота оседания H = 0,1 м; вязкость η = 1·10^-3 Па·с

Таблица 1. Данные седиментационного анализа суспензии песка в воде

Время оседания для точки, к которой проведена касательная, t, мин	Содержание фракции Q, %	Нарастающее суммарное содержание частиц, %	Эквивалентный радиус r·10^6, м
	12,9		19,0
	42,3	87,1	11,0
	17,8	44,8	8,0
	27,0	27,0	6,6
	13,7	13,7	6,0
	7,7	7,7	5,4
	2,0	2,0	4,9

Решение: По уравнению (12) рассчитывают по экспериментальным данным радиус частиц. Для построения интегральной кривой подсчитывают нарастающее суммарное содержание частиц, начиная с самых мелких. По полученным данным (см. табл 1. строят интегральную кривую распределения частиц. Обрабатывая интегральную кривую, получают данные для построения дифференциальной кривой, помещенные в таблице.2.

Таблица 2. Данные для построения дифференциальной кривой распределения частиц песка в воде

r ·10^6, м	Δ r ·10^6, м	ΔQ, %	ΔQ,/ Δ r
	-	-	-
			0,5
		0,5	0,25

Интегральная и дифференциальная кривые распределения изображены на рис.1.

Рис 1.Интегральная и дифференциальная кривые.

Дата добавления: 2015-08-31