Задачник по коллоидной химии

Ответ

Ответ

Используя обществоведческие знания, перечислите три других источника права.

Укажите три признака, по которым вы это определили.

Речь идет о правовом (судебном) прецеденте. Это можно определить, исходя из сущности прецедента – решение государственного органа, которое принимается как образец (в данном случае – разъяснение Верховного суда) при последующем рассмотрении аналогичных дел

В качестве других источников права могут быть перечислены: правовой обычай; нормативно – правовой акт; договор с нормативным содержанием и др.

1. С 7 Лицо, впервые совершившие правонарушение небольшой тяжести, может быть освобождено от юридической ответственности и наказания, если оно примирилось с потерпевшим и возместило причиненный ему вред. Означает ли это, что в результате подобного акта совершенное деяние перестало быть противоправным и общественно опасным? Свой ответ аргументируйте. Используя знания курса обществознания и учитывая содержание задания, назовите любые три освобождения от юридической ответственности и наказания

Освобождение лица от юридическое ответственности не означает, что совершенное им деяние перестало быть противоправным и общественно опасным. Но в силу ряда причин теряется смысл дальнейшего претерпевания лицом мер оказываемого на него воздействия

В качестве оснований освобождения от юридической ответственности и наказания могут быть названы: деятельное раскаяние лица; примирение с потерпевшим; в связи с истечением акта амнистии или помилования и др.

Барнаул – 2003

Содержание

Варианты задач 3

Глава 1.. Молекулярно-кинетические свойства дисперсных систем 4

Глава 2. Седиментация в дисперсных системах 10

Глава 3. Оптические свойства дисперсных систем 21

Глава 4. Поверхностные явления 28

Глава 5. Адсорбция газов и паров на поверхности твердых тел.

Адсорбция из растворов на поверхности твердых тел 38

Глава 6. Электрокинетические явления в дисперсных системах 51

Глава 7. Строение мицеллы гидрофобного золя. Коагуляция гидрофобного золя 62

Используемая литература 68

Варианты задач

№ варианта	Глава 1	Глава 2	Глава 3	Глава 4	Глава 5	Глава 6	Глава 7
		2, 28		4, 12
		3, 29		5, 30
		4, 30		6, 31
		5, 31		7, 32
		6, 32		8, 33
		7, 33		9, 34
		8, 1		10, 35
		9, 2		11, 36
		10, 3		12, 37
		11, 4		13, 38
		12, 5		14, 39
		13, 6		15, 40
		14, 7		16, 41
		15, 8		17, 42
		16, 9		18, 43
		17, 10		19,1
		18, 11		20, 2
		19, 12		21, 3
		20, 13		22, 4
		21, 14		23, 5
		22, 15		24, 6
		23, 16		25, 7
		24, 17		26, 8
		25, 18		27, 9
		26, 19		28, 10
		27, 20		29, 11

Глава 1. Молекулярно-кинетические свойства дисперсных систем

Молекулярно- кинетическая теория изучает законы самопроизвольного движения молекул. Некоторые свойства растворов обусловлены этим движением, т. е. Определяются не составом, а числом кинетических единиц- молекул в единице объема или массы. Коллоидно-дисперсные и микрогетерогенные системы обычно характеризуются дисперсностью, в качестве меры которой принята удельная поверхность. Удельная поверхность дисперсной фазы, содержащей одинаковые частицы, вычисляется по формуле:

(1)

Где S_ч – поверхность частицы, V_ч – ее объем.

К молекулярно- кинетическим свойствам дисперсных систем относятся: броуновское движение, осмос, диффузия.

Диффузией называется процесс самопроизвольного выравнивания концентраций в системе, приводящий к установлению одинакового химического потенциала каждого компонента во всех элементах объема системы. Для описания диффузии используется первый закон Фика:

(2)

где – поток вещества, определяемый как количество вещества dm,

проходящего за время dt через поверхность S, D – коэффициент диффузии, grad C – градиент концентраций.

Осмос- это самопроизвольное проникновение растворителя в раствор, отделенный от него полупроницаемой перегородкой. В дальнейшем этот поток уравновешивается возникающим встречным градиентом давления. Этот процесс обусловлен, в термодинамической трактовке, ростом энтропии системы, а в кинетической, - избыточным числом ударов молекул растворителя о мембрану со стороны более разбавленного раствора. Принципиально осмос в дисперсных системах и растворах высокомолекулярных соединений не отличается от осмоса растворов низкомолекулярных соединений.

(3)

где - частичная концентрация – это число частиц в единице объема,

, k – постоянная Больцмана.

Осмотическое давления золей очень малая величина. Это объясняется чрезвычайно малыми значениями частичной концентрации или, иными словами, чрезвычайно большими значениями частичного веса коллоидных частиц по сравнению с молекулярным. Для двух систем при одной температуре:

(4)

Осмотическое давление не постоянная величина. Это объясняется явлением агрегации, характерным для дисперсных систем:

(5)

Совместное рассмотрение явления осмоса и диффузии приводит к выводу уравнения Эйнштейна:

, (6)

где - константа Больцмана, B – коэффициент вязкого сопротивления среды.

Для сферических частиц:

(7)

где η - вязкость среды, r – радиус частицы. Поэтому для сферических частиц коэффициент диффузии может быть вычислен по формуле:

, [ ] (8)

Источником броуновского движения являются не внешние причины, а внутренние, присущие системе. Иными словами, движение обусловлено столкновениями молекул среды (жидкости или газа) со взвешенными в ней частицами. Броуновское движение частиц описывается уравнением Эйнштейна – Смолуховского:

(9)

где 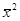- средний квадрат смещения частицы вдоль любой оси за время t. Для расчета 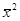проводятся измерения через равные промежутки времени смещения частицы по произвольно выбранному направлению x₁, x₂, x₃,….,x_i …. Затем находятся квадраты этих смещений x₁², x₂²,…,x_i²,… и среднее значение квадрата:

(10)

Кроме поступательного, существует вращательное броуновское движение. В этом случае находится средний квадрат случайного поворота частицы вокруг оси , который также зависит от выбранных промежутков времени:

(11)

Где Θ - коэффициент вращательной диффузии.

Для сферических частиц коэффициент вращательной диффузии определяют по формуле:

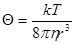(12)

Примеры решения задач:

1. Суспензия кварца содержит сферические частицы, причем 30% массы приходится на частицы, имеющие радиус 1·10^-5 м, а масса остальных – на частицы радиуса 5·10^-5 м.Какова удельная поверхность кварца?

Решение. Обозначим: r₁ – радиус более крупных частиц, r₂ – радиус более мелких частиц, S₁ – суммарная поверхность крупных частиц, S₂ – суммарная поверхность мелких частиц, V₁ – объем крупных частиц, V₂ – объем мелких частиц. Примем V₁ =0,7м³, а V₂ =0,3м³, т. е. V₁ + V₂ =1м³ .

Находим числа частиц в объемах V₁ и V₂:

;

и их суммарные поверхности:

;

;

Удельную поверхность находим как сумму S₁ + S₂, так как V₁+ V₂ =1м³.

;

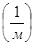
2. Определите коэффициент диффузии красителя конго красный в водном растворе, если при градиенте концентрация 0,5 кг/м³ за 2 ч через 25·10^-4 м² проходит 4,9·10^-7 г вещества.

Решение. Коэффициент диффузии находим из первого закона Фика:

,

где Δm - масса вещества, S – площадь, Δt - время, grad C – градиент концентрации:

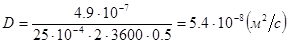
3. Определите радиус частиц золя иодида серебра, используя следующие данные: коэффициент диффузии равен 1,2·10^-10 м²/с, вязкость среды – 10^-3 H·c/м²,температура – 298 K.

Решение: Определяем радиус по формуле (9):

;

4. Рассчитайте среднее квадратичное смещение аэрозольной частицы за 15 с по следующим данным: радиус частицы – 10^-8 м, вязкость среды – 1,9·10^-7 H·c/м², температура – 298 K.

Решение: Используя формулу (10) для среднеквадратичного сдвига, получим:

; .

Дата добавления: 2015-08-31