Седиментационно-диффузионное равновесие

Задачи

1. Определите удельную поверхность следующих частиц?: а) куб с длиной ребра 1 мкм (10^-6 м), б) шар с диаметром 1 мкм, в) цилиндр с высотой и диаметром основания по 1 мкм.

2. Определите дисперсность фазы, состоящей из сферических частиц и характеризующейся следующими данными:

Радиус частиц, мкм
Относительная масса частиц данного радиуса %

3. Рассчитайте коэффициент диффузии коллоидного золота при 20°С в воде, если радиус его частиц равен 10^-9 м, вязкость равна 0,001 Н·с/м².?

4. Определите коэффициент сопротивления при движении частицы кварца в воде, если коэффициент диффузии равен 2.1·10^-12 м²/с, температура равна 25°С.?

5. Определите коэффициент диффузии частицы золота, если при изучении броуновского движения этой частицы вдоль оси через каждые 2с определялись смещения, которые оказались равными (в мкм): 1, 2, 2, 3, 1, 1, 2, 2, 1, 2, 3, 2, 1, 2, 3.?

6. Коэффициент диффузии сферической частицы равен 2.1·10^-11 м²/с, а радиус ее равен 1,4·10^-8 м. Рассчитайте коэффициент вращательной диффузии.?

7. Характеристикой устойчивости дисперсных систем против действия силы тяжести является гипсометрическая высота, равная расстоянию между двумя горизонтальными слоями, на которой концентрация частиц уменьшается в 2 раза. Вычислите гипсометрическую высоту золя золота (плотность золота равна 19300 кг/м³; радиус частиц равен 4·10^-9 м) при 25°С.

8. Вычислить величину среднего сдвига коллоидных частиц гидрозоля гидрата окиси железа при 293° за время τ = 4 сек.,если радиус частиц r=10^-8 м, вязкость воды η = 10^-3 н·сек/м².

9. Найти отношение величин среднего сдвига частиц с радиусами r=2·10^-9 м и

r=2·10^-7 м.

10. Вычислить средний сдвиг частиц эмульсии с радиусом r=6,5·10^-6 м за время τ= 1 сек, вязкость среды η=10^-3 н·сек/м², температура Т = 288°.

11. Вычислить коэффициент диффузии частиц золя сернистого мышьяка с радиусом частиц к=20·10^-9м, вязкость среды η=10^-3 н·сек/м², температура Т = 288°.

12. Найти коэффициент диффузии частиц высокодисперсной фракции суспензии глины в воде при радиусе порядка 10^-7 м. Вязкость среды η=6,5·10^-4 н·сек/м², температура Т = 313°.

13. Вычислить коэффициент диффузии частиц дыма окиси цинка при радиусе

r=2·10^-6 м и вязкости воздуха η=1,7·10^-5 н·сек/м², температура Т =283°.

14. Вычислить коэффициент диффузии частиц высокодисперсного аэрозоля с радиусом частиц r=2·10^-8 м при Т = 293°. Вязкость воздуха η=1,8·10^-5 н·сек/м².

15. С какой скоростью будут оседать капли водяного тумана с радиусами частиц

r₁=10^-4 м, r₂=10^-6 м Вязкость воздуха η=1,8·10^-5 н·сек/м². Величиной плотности воздуха пренебречь.

16. Вычислить скорость оседания аэрозоля хлористого аммония (плотность d=1,5·10³ кг/м³) с частицами м. Вязкость воздуха н·сек/м². Величиной плотности воздуха пренебречь.

17. Найти скорость оседания частиц суспензии каолина в воде при 288°. Радиус частиц 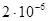м, плотность каолина d = 2,2·10³ кг/м³, вязкость воды 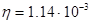н·сек/м².

18. Найти величину коэффициента диффузии мицелл мыла в воде при 313° и среднем радиусе мицелл 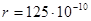м. Вязкость воды 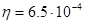н·сек/м², постоянная Больцмана 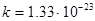дж/град.

19. Вычислить величину осмотического давления дыма мартеновских печей концентрации 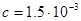кг/м³. Средний радиус частиц аэрозоля м, плотность 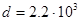кг/м³, Т = 293°.

20. Определить осмотическое давление гидрозоля золота концентрации с= 2 кг/м³ с диаметром частиц 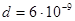м и плотностью 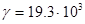кг/м³, Т =293°.

21. Сравнить осмотическое давление золя с частицами радиуса порядка 10^-8 м с осмотическим давлением молекулярного раствора (радиус молекул имеет порядок 10^-10 м). Плотность золя равна плотности раствора.

23. Рассчитать величину осмотического давления золя сернистого мышьяка As₂S₃ концентрации с =7 кг/м³. Средний радиус частиц 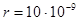м, плотность золя d = 2,8·10³ кг/м³, Т = 293°.

24. Рассчитать и сравнить осмотическое давление двух гидрозолей сернистого мышьяка As₂S₃ одинаковой концентрации и различной дисперсности: 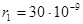м, м.

25. Показать изменение величины коэффициента диффузии частиц красителя прямого голубого в воде при добавлении к нему диспергатора, используя следующие экспериментальные данные: радиус частиц красителя без добавки диспергатора r₁ = 16-10^-10 м, с добавкой диспергатора г₂= 9,6-10^-10 м. Вязкость воды при Т = 298 K, η=8,94·10^-4 н·сек/м², постоянная Больцмана k = 1,ЗЗ·10^-23 дж/град.

26. Построить кривую изменения величины коэффициента диффузии красителя прямого голубого в воде с увеличением температуры, используя следующие экспериментальные данные:

T,K	Средний радиус частиц, 10^-10, м	Вязкость воды (η) 10^-4 н·сек/м^2
	15,9	8,94
	11,95	7,21
	9,75	4,70
	8,51	3,60

Глава 2. Седиментация в дисперсных системах

Частицы дисперсной фазы в гравитационном поле оседают, если их плотность больше плотности дисперсионной среды, или всплывают, если их плотность меньше плотности дисперсионной среды. Следствием процесса седиментации является возникновение градиента концентраций частиц по высоте сосуда, приводящего к диффузии, направленного в сторону меньшей концентрации.

Сравнение седиментационного (i_сед) и диффузионного (i_диф) потоков позволяет установить, какой из процессов преобладает в данной дисперсной системе.

Для нахождения закона распределения частиц по высоте исходят из равенства потоков диффузии и седиментации (i_сед = i_{диф) ,} т.е. из условия седиментационно – диффузионного равновесия. Поток седиментации рассчитывают по уравнению

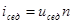(1)

где u_сед - линейная скорость седиментации; п - число частиц в единице объема (частичная концентрация).

Условием равномерного движения частицы является равенство силы тяжести и силы трения; последняя для сферической частицы радиуса r определяется по уравнению Стокса;

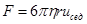(2)

Скорость седиментации с учетом поправки на потерю в массе по закону Архимеда выразится уравнением

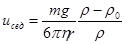(3)

где т— масса частицы; g - ускорение свободного падения; ρ и ρ₀ - плотность дисперсной фазы и дисперсионной среды.

Диффузионный поток рассчитывают по уравнению Фика:

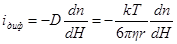(4)

Здесь - градиент концентрации по высоте H.

Приравняв правые части уравнений (4) и (5), получают выражение седиментационно - диффузионного равновесия, называемое уравнением Лапласа—Перрена:

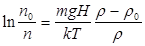(5)

где п и п₀ - число частиц на исходном уровне и на высоте H соответственно.

Уравнение (5) является частным случаем универсального закона распределения Больцмана:

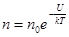(6)

где U— потенциальная энергия; для гравитационного поля с учетом поправки по закону Архимеда:

(7)

Уравнение (5) было получено раньше независимо от закона Больцмана.

Определение размеров частиц может быть проведено двумя методами: по измерению скорости седиментации и на основании исследования распределения частиц по высоте. Первый метод широко используется для грубодисперсных систем с размерами частиц более 10^-6м. На этом методе основан седиментационный анализ грубодисперсных систем.

Второй метод определения размеров частиц - по седиментационно-диффузионному равновесию - непригоден для грубодисперсных систем (там практически отсутствует поступательное броуновское движение). Для коллоидных систем (размеры частиц 10^-7 – 10^-9м) этот метод в гравитационном поле практически не используется, так как здесь существенно преобладает тепловое движение частиц над седиментацией.

Расчет показывает, что частицы размером 10^-7—10^-9 м удерживаются тепловым движением во взвешенном состоянии. Их концентрация во всем объеме остается практически постоянной - такие системы седиментационно устойчивы.

Метод определения размеров частиц по седиментационно-диффузионному равновесию успешно используется с применением центробежного поля, при этом регулирование скорости вращения центрифуги позволяет применять этот метод в достаточно большом интервале размеров. Используя ультрацентрифугу, можно определять также молекулярную массу полимеров.

Дата добавления: 2015-08-31