Построение интегральных и дифференциальных кривых распределения частиц

Для построения интегральной (суммарной) кривой распределения частиц по радиусам рассчитывают содержание отдельных фракций (в %):

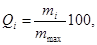(13)

где т_i — масса частиц данной фракции. Очевидно, Q₁ + Q₂ +…+ Q_n = 100%

При построении интегральной кривой (рис. 3.1) на оси абсцисс откладывают значения эквивалентных радиусов, начиная с радиусов самых мелких частиц, а на оси ординат - нарастающее суммарное содержание (в %) всех частиц от наименьшего до данного радиуса включительно, относя его к наибольшему в данной фракции радиусу. Например, содержание частиц самой мелкой фракции (меньше радиуса r_n)составляет Q_n; для частиц следующей, более крупной фракции (радиусы частиц от r_п до r_п-1)суммарное содержание равно Q_n + Q_n-1 и т. д.

Таким образом, последняя суммарная величина Q, соответствующая фракции от r₁ до r_max и отнесенная r_max. составит 100% (рис. 3.1).

Эквивалентный радиус, соответствующий наиболее часто встречающемуся размеру частиц в данной системе, находят из дифференциальной кривой распределения, для построения которой обрабатывают интегральную кривую следующим образом (рис. 3.2): через равные интервалы радиусов Δ r, которые выбираются произвольно, строят ординаты до пересечения с интегральной кривой, сносят эти точки на ось ординат и находят значение Δ Q - разности между двумя соседними ординатами. Число отрезков Δ r на которые разбивают абсциссу, должно быть не менее 8 - 10.

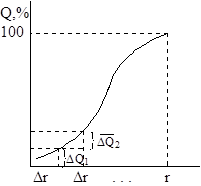
Рис. 1.3. Интегральная кривая распределения	Рис 2.3. Обработка интегральной кривой для построения дифференциальной кривой распределения

Затем, откладывая на оси абсцисс значения эквивалентных радиусов r, а на оси ординат – Δ Q /Δ r, строят прямоугольники, беря за основания равные интервалы радиусов Δ r, а за высоту Δ Q /Δ r (рис. 3.3).

Рис. 3.1.Дифференциальная кривая распределения

В полученной гистограмме площадь каждого прямо угольника представляет собой содержание фракции осадка в пределах выбранного интервала радиусов Δ r. Соединив плавной кривой середины верхних оснований прямоугольников, получают дифференциальную кривую распределения, по которой можно определить r_н.в — наиболее вероятный радиус частиц в данной дисперсной системе.

По форме дифференциальная кривая чаще всего представляет собой статистическую кривую распределения с одним максимумом, но она может иметь и другую форму, это зависит от характера дисперсности системы.

Возможные ошибки при использовании графического метода расчета кривых распределения связаны с неточ­ностью и некоторой субъективностью проведения каса­тельных к кривой, особенно в области, близкой к насы­щению (где кривая переходит в горизонтальную прямую). Кроме того, необходимость построения всей седиментационной кривой требует иногда значительного времени для проведения эксперимента, причем не всегда удается довести оседание самых мелких частиц до конца. Однако графи­ческий метод широко используется в практике, так как он прост и нагляден. Возможные ошибки графического дифференцирования могут быть уменьшены применением приборов, осуществляющих автоматическое измерение и запись производных по седиментационной кривой.

Дата добавления: 2015-08-31