Загальна дисперсія, семіваріація плюс, семіваріація мінус

Дисперсія часто застосовується в теорії ймовірностей і математичній статистиці. Означає ступінь розсіювання навколо середнього значення випадкової величини. У статистичному розумінні дисперсія є середнє арифметичне із квадратів відхилень величин від їх середнього арифметичного. На практиці часто необхідно оцінити розсіювання можливих значень випадкової величини навколо її середнього значення, а також виявити та виміряти силу зв'язку між факторними та результативною ознаками [3]. З рисунку видно, що найкращою є стратегія S5.

Dj

104,8333

180,1333

111,3667

109,5333

80,26667

Рис 1.2 Значення дисперсії для кожної стратегії

У неокласичній теорії економічного ризику виходять з того, що ризик пов’язаний лише з несприятливими для менеджера (інвестора) ефектами і для його оцінювання достатньо брати до уваги лише несприятливі відхилення від сподіваної величини. При цьому в якості міри ризику використовується семіваріація.

Показник семіваріації характеризує тільки додатні або тільки від’ємні відхилення від математичного сподівання. Додатня семіваріація розраховується за формулою:

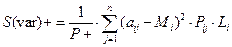Додатня семиваріація характеризує середній квадрат відхилення тих значень прибутку, які більше від середнього. Чим менша додатня семіваріація, тим менший ризик і більший шанс отримати більше ніж запланували. Необхідно взяти ті умови стратегії, які більші за математичне сподівання, відняти від них саме математичне сподівання. Потім різницю піднести до квадрату і помножити на ймовірність взятої умови, а потім скласти різниці умов з математичним сподіванням піднесеного до квадрату і помножене на ймовірність. Для інших стратегій розраховується аналогічно. Додатня семіваріація характеризує середній квадрат відхилення тих значень прибутку, які більше від середнього. Чим менша додатня семіваріація, тим менший ризик і більший шанс отримати більше ніж запланували. У нашому випадку має найменший ризик стратегія S2.

Від’ємна семіваріація розраховується за формулою:

Від’ємна семіваріація характеризує середній квадрат відхилення тих значень прибутку, які менші від середнього. Чим більша від’ємна семіваріація, тим більший ризик і менший шанс отримати прибуток. S5 має найменший ризик.

Табл. 1.2

Дата добавления: 2015-08-31