Шаг 3. Нахождение площади сечения

Шаг 2. Нахождение сторон треугольника.

Решение. Шаг 1. Построение сечения

Изобразите сечение правильной шестиугольной призмы, все ребра которой равны 1, проходящее через вершины, и. Найдите его площадь.

ПОСТРОЕНИЕ СЕЧЕНИЙ.

ПРАВИЛЬНАЯ ШЕСТУГОЛЬНАЯ ПРИЗМА.

Строим призму и отмечаем на ней точки, через которые, по условию, проходит сечение.
Среди этих точек находим пары тех, которые лежат в одной плоскости, и соединяем их отрезками.

Полученный в результате построений треугольник 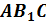будет искомым сечением.

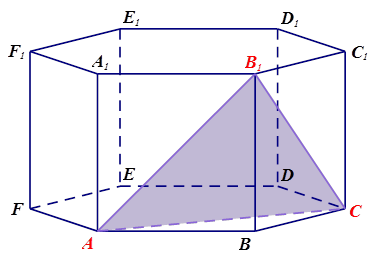
Чтобы найди длины сторон полученного треугольника, необходимо для каждой из них рассмотреть плоскость грани призмы, в которой она лежит.

	I способ: Рассмотрим 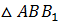(). По теореме Пифагора: II способ: – диагональ квадрата. Поэтому можно воспользоваться формулой:
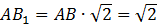
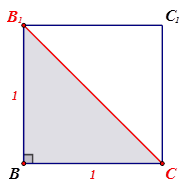
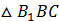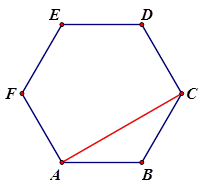
	I способ: Рассмотрим (). По теореме Пифагора: II способ: – диагональ квадрата. Поэтому можно воспользоваться формулой:
	– малая диагональ правильного шестиугольника. Поэтому мож­но воспользоваться формулой:

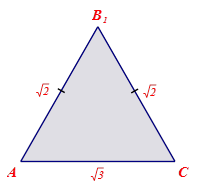Сечение представляет собой равнобедренный треугольник , в котором – основание, а и – боковые стороны. Проверим, будет ли треугольник прямоугольным.

Для этого сравним и :

Следовательно, – остроугольный.

Для нахождения площади сечения воспользуемся формулой:

Проведем высоту . Т.к. равнобедренный, то – медиана, т.е.:

Из прямоугольного треугольника по теореме Пифагора:

Дата добавления: 2017-01-13