Построить картину нулей и полюсов на комплексной z-плоскости

Найти значения нулей и полюсов.

Записать выражения для передаточной функции звена.

Передаточная функция каскадно реализуемого РФ определяется произведением передаточных функций его звеньев [1 c.87]:

где H_J(z) - передаточная функция J-го биквадратного звена при значении коэффициента b_0J = 1; при b_0J ¹ 1 добавляется общий нормирующий или масштабирующий множитель С₀.

Её можно представить произведением передаточных функций нерекурсивной и рекурсивной части [2 c.15]:

Подставив значения коэффициентов b₀, b₁, b₂, a₁, a₂, получаем:

Значения нулей z₀ и полюсов z_p в алгебраической форме можно определить по формулам [1 c.87]:

В результате расчетов получаем:

Для представления нулей и полюсов в показательной форме найдём модуль и аргумент комплексного числа по формулам:

Получаем:

По результатам расчётов построим картину нулей и полюсов (рис. 3). Данный графический способ удобен для качественной оценки частотной характеристики и частотных свойств по значению нулей и полюсов. Минимальному расстоянию r_p от точки на единичной окружности с частотой ω до полюсов соответствуют максимальные значения АЧХ или коэффициента передачи РФ. Минимальному расстоянию до нулей r₀ - минимальные значения коэффициента передачи фильтра. Таким образом, положение полюсов определяет полосу пропускания частотной характеристики фильтра, а положение нулей – ее полосу задерживания. По картине нулей и полюсов на комплексной плоскости также судят об устойчивости РФ. Полюсы устойчивого РФ, не превышающие по модулю единицу (| z_pi | < 1), находятся внутри круга единичного радиуса.

Рисунок 3 − Картина нулей и полюсов

7. По картине нулей и полюсов графически (приближенно) найти зависимость коэффициента передачи фильтра от нормированной (цифровой) частоты λ = ωТ_Д, изменяемой в пределах от 0 до π (амплитудно-частотную характеристику фильтра - АЧХ); определить и отметить максимум коэффициента передачи и значение частоты λ_max, на которой он имеет место.

АЧХ фильтра можно найти по формуле [1 c.84]:

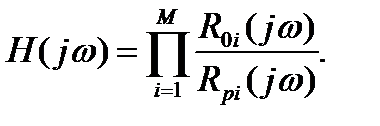
где R_0i и R_pi представляют векторные расстояния от точки на единичной окружности с угловой координатой λ=wT_д соответственно до нулей z_0i и полюсов z_pi РФ;

М − количество нулей и полюсов равно 2.

Координаты точки А, находящейся на единичной окружности комплексной плоскости находятся по формуле:

Расстояние между двумя точками А и В находится по формуле:

Рассчитаем значения 6 точек для λ от 0 до π и для частот нулей и полюсов. Результаты расчётов показаны в таблице 1. График АЧХ показан на рис. 4.

Таблица 1 − Результат рассчёта АЧХ рекурсивного ЦФ

λ=ωТД		0,69813	π/2	2,32711	2,8	π
А(λ)	3,49743	2,9865	1,37235	6,145∙10^-6	0,49479	0,60522

Рисунок 4 − АЧХ рекурсивного цифрового фильтра

По виду АЧХ такой фильтр можно отнести к ФНЧ [3 c.115]. Его коэффициент передачи имеет максимум на частоте λ=0, на частотах нулей λ=2,32711 коэффициент передачи равен 0 (бесконечное затухание АЧХ).

8. Записать аналитические выражения для частотной характеристики нерекурсивной, рекурсивной частей и всего фильтра и рассчитать их АЧХ для значений нормированной частоты λ в диапазоне от 0 до π. Показать, как они преобразуются в АЧХ, зависящую от физической частоты f, задавшись значением частоты дискретизации f_д из исходных данных к лабораторным работам.

Выражения для частотной характкристики получаются из передаточной функции H(z)=H_H(z)∙H_P(z) путём замены z на e^iλ [2 c.16]. Получаем:

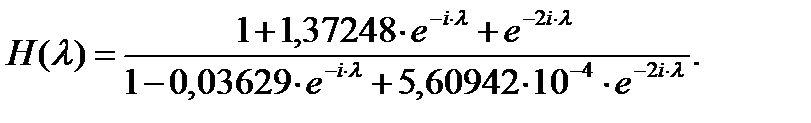(3)

где − частотная характеристика нерекурсивной части;

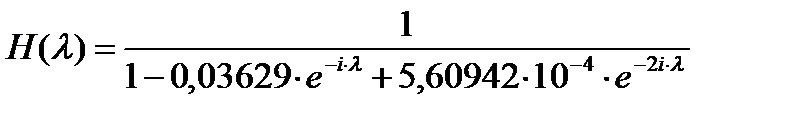− частотная характеристика рекурсивной части.

Графики АЧХ нерекурсивной, рекурсивной частей и всего фильтра изображены на рис. 5-7.

Рисунок 5 − АЧХ нерекурсивной части цифрового фильтра

Рисунок 6 − АЧХ рекурсивной части цифрового фильтра

Рисунок 7 − АЧХ всего фильтра

Чтобы получить АЧХ Н(f), зависящую от физической частоты f, нужно в выражение (3) для частотной характеристики вместо λ подставить 2π f/ f_Д, и задаться значением частоты дискретизации f_Д. Графики АЧХ Н(f) при f_Д=7680 Гц и f_Д=112 кГц изображены на рис. 8,9.

Рисунок 8 − АЧХ фильтра при f_Д=7680 Гц

Рисунок 9 − АЧХ фильтра при f_Д=112 кГц

Исходя из графиков, изображённых на рис. 8,9, можно сделать вывод, что от абсолютного значения частоты дискретизации ω_Д не зависит частотная характеристика ЦФ, заданная функцией цифровой частоты l: H(jλ) = H(jωT_д). Это означает, что ЦФ с центральной частотой l₀ частотной характеристики H(jλ) будет откликаться на дискретные сигналы с частотами ω_0i = λ₀f_дi, соответствующими различным значениям частот дискретизации f_дi этих сигналов.

Дата добавления: 2017-01-13