Привести графики ИХ нерекурсивной части, рекурсивной части и всего фильтра. Оценить приближенно длительность переходных процессов в фильтре

Найти аналитические выражения для импульсной характеристики (ИХ) нерекурсивной и рекурсивной частей фильтра, показать, как по ним найти ИХ всего фильтра.

Аналитические выражения для импульсной характеристики (ИХ) [2 c.16] −

для нерекурсивной части h_H(0) = b₀ = 1; h_H(1) = b₁ = 1,37248; h_H(2) = b₂ = 1, а для его рекурсивной части аналитическое выражение ИХ в случае простых комплексно-сопряжённых полюсов можно привести к виду:

ИХ всего фильтра является свёрткой ИХ нерекурсивной и рекурсивной части:

Расчёт ИХ сделаем в mathcad. Полученные графики изображены на рис. 10-12.

Рисунок 10 − ИХ нерекурсивной части

Рисунок 11 − ИХ рекурсивной части

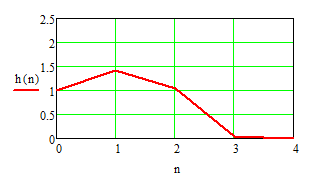
Рисунок 12 − ИХ всего звена

Начиная с 4-го отсчёта модуль импульсной характеристики не превышает 7,6529∙10^-4, которое более чем в 100 раз меньше максимального значения h(1) = 1,40877. Поэтому реальную длительность переходного процесса и реальную длительность импульсной характеристики фильтра можно принять равной 4.

11. В соответствии с разностным уравнением найти отклики фильтра на входные воздействия типа единичный импульс и единичный скачок для n=0,1, 2,.. 9, построить графики откликов.

Отклики фильтра находятся при нулевых начальных условиях, соответствующих: x(–1) = x(–2) = y(–1) = y(–2) = 0.

Для прямой формы реализации отклик ЦФ на единичный импульс показан в табл. 2. Отклик на единичный скачок показан в табл. 3.

Таблица 2 − Отклик ЦФ для прямой формы реализации (единичный импульс)

n	x(n)	x(n-1)	x(n-2)	y(n-1)	y(n-2)	y(n)
						1,40877
				1,40877		1,05056
				1,05056	1,40877	0,03734
				0,03734	1,05056	7,6661∙10^-4
				7,6661∙10^-4	0,03734	6,91207∙10^-6
				6,91207∙10^-6	7,6661∙10^-4	-1,78462∙10^-7
				-1,78462∙10^-7	6,91207∙10^-6	-1,03472∙10^-8
				-1,03472∙10^-8	-1,78462∙10^-7	-2,7556∙10^-10
				-2,7556∙10^-10	-1,03472∙10^-8	-4,20565∙10^-12

Таблица 3 − Отклик ЦФ для прямой формы реализации (единичный скачёк)

n	x(n)	x(n-1)	x(n-2)	y(n-1)	y(n-2)	y(n)
						2,40877
				2,40877		3,45933
				3,45933	2,40877	3,49667
				3,49667	3,45933	3,49744
				3,49744	3,49667	3,49744
				3,49744	3,49744	3,49744
				3,49744	3,49744	3,49744
				3,49744	3,49744	3,49744
				3,49744	3,49744	3,49744

Для канонической формы реализации отклик ЦФ на единичный импульс показан в табл. 4. Отклик на единичный скачок показан в табл. 5. Отклики фильтра находятся при нулевых начальных условиях, соответствующих: w(–1) = w(–2) = 0.

Таблица 4 − Отклик ЦФ для канонической формы реализации (единичный импульс)

n	x(n)	w(n-1)	w(n-2)	w(n)	y(n)
				0,03629	1,40877
		0,03629		7,56964∙10^-4	1,05056
		7,56964∙10^-4	0,03629	7,14783∙10^-6	0,03734
		7,14783∙10^-6	7,56964∙10^-4	-1,64505∙10^-7	7,6661∙10^-4
		-1,64505∙10^-7	7,14783∙10^-6	-9,97268∙10^-9	6,91207∙10^-6
		-9,97268∙10^-9	-1,64505∙10^-7	-2,69786∙10^-10	-1,78462∙10^-7
		-2,69786∙10^-10	-9,97268∙10^-9	-4,20582∙10^-12	-1,03472∙10^-8
		-4,20582∙10^-12	-2,69786∙10^-10	-1,54923∙10^-15	-2,7556∙10^-10
		-1,54923∙10^-15	-4,20582∙10^-12	2,29904∙10^-15	-4,20565∙10^-12

Таблица 5 − Отклик ЦФ для канонической формы реализации (единичный скачёк)

n	x(n)	w(n-1)	w(n-2)	w(n)	y(n)
				1,03629	2,40877
		1,03629		1,03705	3,45933
		1,03705	1,03629	1,03705	3,49667
		1,03705	1,03705	1,03705	3,49744
		1,03705	1,03705	1,03705	3,49744
		1,03705	1,03705	1,03705	3,49744
		1,03705	1,03705^-9	1,03705	3,49744
		1,03705	1,03705^-10	1,03705	3,49744
		1,03705^15	1,03705	1,03705	3,49744

Сравнивая значения на выходе цифрового фильтра y(n) для разных реализаций, можно сделать вывод, что они идентичны.

Дата добавления: 2017-01-13