Рассчитать приближенно масштабные множители звена временным, статистическим и спектральным методами

Масштабные множители (ММ) m_i выбирают так, чтобы амплитуды сигналов на выходах сумматоров или звеньев v_i(n) при максимальном значении сигнала на входе фильтра x(n), равном единице (|x(n)|max= 1), не превышали по модулю некоторого максимального значения, принимаемого также обычно за единицу (|v_i(n)|max= 1) [1 c.144].

Масштабные множители можно рассчитать тремя способами. Временной способ:

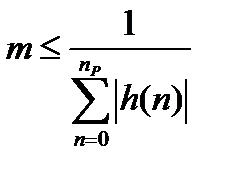
где n_p − число отсчетов всего фильтра

h(n) − импульсная характеристика

Статистический метод:

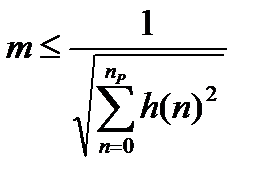
Спектральный метод:

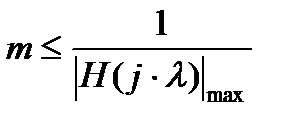
где H(j∙λ) − максимальное значение АЧХ (находится примерно на частоте полюса λ_Р.

Получаем для прямой формы реализации временным методом:

m≤ 0,28592.

Статистическим методом:

m≤ 0,49449.

Спектральным методом:

m≤ 0,33484.

Для канонической формы реализации ЦФ необходимо исключить переполнение в обоих сумматорах. Для второго сумматора импульсная и частотная характеристики, используемые для расчёта масштабных множителей, является импульсная и частотная характеристика всего звена, а для первого сумматора импульсная и частотная характеристики рекурсивной части.

Временной способ:

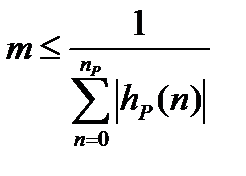
где n_p − число отсчетов всего фильтра

h_Р(n) − импульсная характеристика рекурсивной части

Статистический метод:

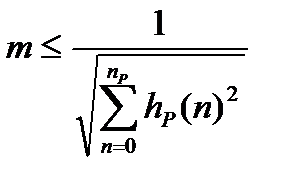
Спектральный метод:

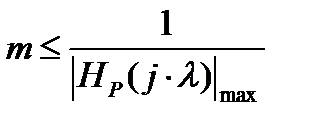
где H_Р(j∙λ) − максимальное значение АЧХ рекурсивной части (находится примерно на частоте полюса λ_Р.

Из двух значений масштабных множителей выбирается наименьший.

Получаем для первого сумматора временным методом:

m≤ 0,96427.

Статистическим методом:

m≤ 0,99934.

Спектральным методом:

m≤ 0,97257.

Временной метод даёт предельную оценку ММ, исключая переполнение при любых сигналах. Спектральный метод даёт удовлетворительную оценку ММ для квазигармонических сигналов и определяет их верхнюю границу. Статистический метод даёт удовлетворительную оценку ММ для широкополосных и случайных сигналов с равномерным энергетическим спектром.

13. Показать форматы двоичных чисел, соответствующих коэффициентам фильтра разрядностью q_к= 16 бит, отсчетам входного сигнала (АЦП) разрядностью q_x = 8 бит и произведений разрядностью q_r = 16 бит.

Так как коэффициенты фильтра по модулю меньше 2, то для их представления в смешанном дробном формате при q_к = 16 необходимы 1 разряд знака q_з, 1 разряд целой части q_ц и 14 разрядов дробной части q_д [2 c.16]:

Таблица 6 − Представление коэффициента b₁ в двоичном виде

2^1

2^0

2^-1

2^-2

2^-3

2^-4

2^-5

2^-6

2^-7

2^-8

2^-9

2^-10

2^-11

2^-12

2^-13

2^-14

Знак

Ц.часть

Дробная часть

Получаем:

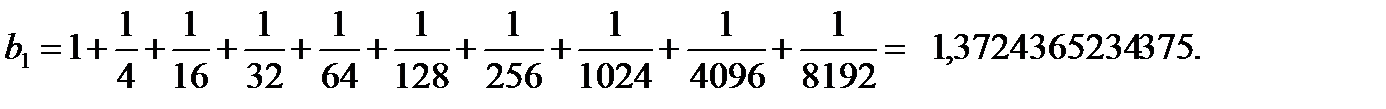
Такой формат обозначается как q_з.q_ц.q_д. = 1.1.14. Соответственно, дробный

формат входного сигнала при q_x = 8 обозначается 1.0.7:

Таблица 7 − Дробный формат входного сигнала при q_x = 8

2^1	2^-1	2^-2	2^-3	2^-4	2^-5	2^-6	2^-7
Знак	Дробная часть

Дробный формат произведений и выходного сигнала при q_r = 16 обозначается 1.0.15.:

Таблица 8 − Дробный формат произведений и выходного сигнала при q_r = 16

2^1

2^-1

2^-2

2^-3

2^-4

2^-5

2^-6

2^-7

2^-8

2^-9

2^-10

2^-11

2^-12

2^-13

2^-14

2^-15

Знак

Дробная часть

14. Найти квантованные значения коэффициентов фильтра при q_к= 16 бит и сравнить их с точными значениями. Объяснить, к чему приводит их различие.

Квантование (ограничение разрядности) коэффициентов до заданного числа двоичных разрядов q_к осуществляется следующим образом [2 c.17]:

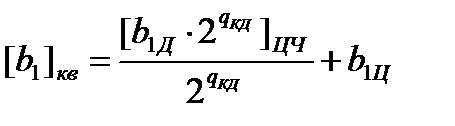
где b_1Ц − целая часть коэффициента b₁

b_1Д − дробная часть коэффициента b₁

q_КД − количество разрядов в дробной части (в нашем случае 14)

ЦЧ − целая часть.

Получаем для коэффициента b₁:

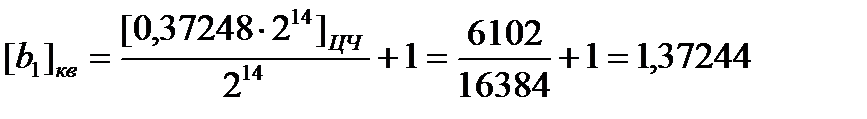
Квантованные значения остальных коэффициентов:

b₀ = 1; b₂ = 1; а₁ = -0,03625; а₂ = 0,00056.

После квантования коэффициентов фильтра они будут отличаться от точных значений, что приведёт к изменению значений нулей и полюсов ЦФ, а это приведёт к отклонению АЧХ и ФЧХ фильтра от заданной. Квантование также может привести к смещению полюсов ЦФ за пределы единичной окружности, что приведёт к потере устойчивости ЦФ. Во избежание этого необходимо постоянно контролировать значения нулей и полюсов фильтра в процессе квантования коэффициентов.

Дата добавления: 2017-01-13