
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Класифікація рівнянь
|
|
|
|
Визначення рівняння другого порядку з двома змінними у частинних похідних.
Лекція №10. Класифікація рівнянь у частинних похідних другого порядку. Диференційні рівняння з двома змінними
Означення. Співвідношення 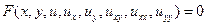 , де х, у незалежні змінні, а и,
, де х, у незалежні змінні, а и,  , функція від х,у, та її частинні похідні,називається рівняння у частинних похідних другого порядку з двома невідомими.
, функція від х,у, та її частинні похідні,називається рівняння у частинних похідних другого порядку з двома невідомими.
Рівняння називається лінійним відносно старших похідних, якщо воно має вид:
 , де а11,а21,а22 – функції від х,у.
, де а11,а21,а22 – функції від х,у.
Рівняння називається лінійним, якщо воно лінійне відносно всіх похідних
 ,
,
де коефіцієнти – функції від х,у.
Якщо f(x,y)=0, то рівняння називається однорідним.
За допомогою перетворень ξ=φ(х,у) η=ψ(х,у) (що має обернене) ми отримаємо нове рівняння еквівалентне даному. Спробуємо спростити рівняння за допомогою переходу до нових змінних.
Враховуючи що:
ux=u ξ ξx+u η ηx
uy= u ξ ξy+u η ηy


uyy – має вигляд uхх при заміні х на у.
Підставивши в рівняння (*), отримаємо:




при цьому  як і
як і  не залежать від других похідних (в випадках лінійного рівняння воно залишається лінійним).
не залежать від других похідних (в випадках лінійного рівняння воно залишається лінійним).
Виберемо ξ та η, щоб  .
.
Розглянемо рівняння з частковими похідними першого порядку 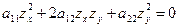 . Якщо
. Якщо  - який-небудь розв’язок цього рівняння, то припускаючи
- який-небудь розв’язок цього рівняння, то припускаючи  отримаємо, що
отримаємо, що  , тобто спрощене рівняння другого порядку зв’язано з розв’язком рівняння першого порядку.
, тобто спрощене рівняння другого порядку зв’язано з розв’язком рівняння першого порядку.
Теорема. Якщо  розв’язок рівняння (**)
розв’язок рівняння (**) 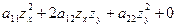 , то
, то  - загальний інтеграл звичайного диференційного рівняння
- загальний інтеграл звичайного диференційного рівняння  .
.
Навпаки, якщо  загальний інтеграл вказаного звичайного диференційного рівняння, то функція
загальний інтеграл вказаного звичайного диференційного рівняння, то функція  - розв’язок диференційного рівняння в часткових похідних першого порядку (**).
- розв’язок диференційного рівняння в часткових похідних першого порядку (**).
Доведення. Якщо  - розв’язок рівняння (**), то рівність являється тотожністю:
- розв’язок рівняння (**), то рівність являється тотожністю:
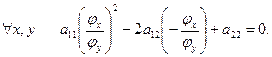
Розглядаючи співвідношення  маємо, що у – неявно задана функція
маємо, що у – неявно задана функція  і
і  .
.
Підставивши в тотожність отримаємо:
 ,
,
тобто  - загальний інтеграл вказаного звичайного диференційного рівняння.
- загальний інтеграл вказаного звичайного диференційного рівняння.
Нехай тепер  - загальний інтеграл звичайного диференційного рівняння. Покажемо, що
- загальний інтеграл звичайного диференційного рівняння. Покажемо, що  .
.
Нехай 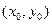 яка-небудь точка. Проведемо через
яка-небудь точка. Проведемо через 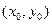 інтегральну криву звичайного диференційного рівняння, припускаючи що
інтегральну криву звичайного диференційного рівняння, припускаючи що  і розглянемо криву
і розглянемо криву  . Для всіх точок цієї кривої
. Для всіх точок цієї кривої
 .
.
Припускаючи що  отримаємо
отримаємо
 , а оскільки
, а оскільки  - довільна точка то рівність виконується для всіх (х,у). Що і треба було довести.
- довільна точка то рівність виконується для всіх (х,у). Що і треба було довести.
Означення. Рівняння  називається характеристичним для диференційного рівняння другого порядку в частинних похідних, а його інтеграли – характеристиками.
називається характеристичним для диференційного рівняння другого порядку в частинних похідних, а його інтеграли – характеристиками.
Припустимо  (φ – загальний інтеграл характеристичного рівняння) ми отримаємо, що
(φ – загальний інтеграл характеристичного рівняння) ми отримаємо, що  . Якщо
. Якщо  являється іншим загальним інтегралом (незалежним від φ), то припускаючи що
являється іншим загальним інтегралом (незалежним від φ), то припускаючи що  ми отримаємо, що і
ми отримаємо, що і 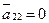 .
.
Очевидно, що характеристичне рівняння розпадається на два рівняння
 (***)
(***)
 .
.
Знак підкорінного виразу визначає тип рівняння
 .
.
1. Якщо 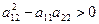 в точці М(х,у), то рівняння називається рівнянням гіперболічного типу.
в точці М(х,у), то рівняння називається рівнянням гіперболічного типу.
2. Якщо 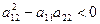 в точці М(х,у), то рівняння називається рівнянням еліптичного типу.
в точці М(х,у), то рівняння називається рівнянням еліптичного типу.
3. Якщо  в точці М(х,у), то рівняння називається рівнянням параболічного типу.
в точці М(х,у), то рівняння називається рівнянням параболічного типу.
Розглянемо кожну ситуацію окремо.
1. 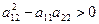 , тоді праві частини (***) дійсні і різні. Розв’язуючи рівняння (***) отримаємо незалежні загальні інтеграли
, тоді праві частини (***) дійсні і різні. Розв’язуючи рівняння (***) отримаємо незалежні загальні інтеграли  та
та  . Припускаючи
. Припускаючи 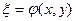
 приводимо рівняння другого порядку до виду
приводимо рівняння другого порядку до виду  .
.
Припускаючи  , де
, де  нові змінні і враховуючи, що
нові змінні і враховуючи, що 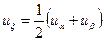 ,
, 
 , рівняння набуває вигляду
, рівняння набуває вигляду  .
.
2.  , тоді рівняння (***) має один розв’язок
, тоді рівняння (***) має один розв’язок  . Покладемо
. Покладемо 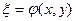 та
та  - довільна функція. Тоді
- довільна функція. Тоді

 .
.
Таким чином, рівняння другого порядку прийме вид  .
.
3. 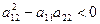 . Нехай
. Нехай 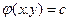 - комплексний інтеграл першого рівняння (***). Тоді
- комплексний інтеграл першого рівняння (***). Тоді  - інтеграл спряженого рівняння 2 з (***). Покладемо
- інтеграл спряженого рівняння 2 з (***). Покладемо 

тоді еліптичне рівняння приводяться до того ж виду що й гіперболічне. Замінимо  тобто
тобто  . Вводячи заміну, отримаємо рівняння
. Вводячи заміну, отримаємо рівняння  .
.
Отже, рівняння другого порядку у частинних похідних з двома змінними (за допомогою заміни незалежних змінних) завжди можна привести до одного з трьох канонічних виглядів:
1. 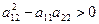 (гіперболічний тип)
(гіперболічний тип) 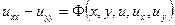 або
або 
2. 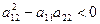 (еліптичний тип)
(еліптичний тип) 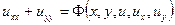
3.  (параболічний тип)
(параболічний тип) 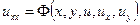
Зауваження. Подібна класифікація має місце і для рівнянь другого порядку з багатьма змінними.
Приклад. Привести до канонічного виду 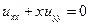 .
.
а11=1, а12=0, а22=х і  .
.
1. Якщо х>0 рівняння еліптичне.
2. Якщо х<0 рівняння гіперболічне.
3. Якщо х=0 рівняння параболічне.
1. х>0, 

 . Отже
. Отже 
 .
.
Тоді  і
і
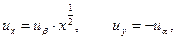

 ,
,

Підставивши в рівняння отримаємо:
 , або
, або
 - еліптичне рівняння
- еліптичне рівняння
2. х=0 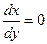 у=с. Отже
у=с. Отже  .
.
Тоді  - довільна і
- довільна і
 ,
, 
Рівняння прийме вид (після заміни)
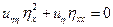 (в х=0),
(в х=0),  - параболічне рівняння.
- параболічне рівняння.
Випадок 3 аналогічний 1.
Зауваження. У випадку постійних коефіцієнтів в лінійному рівнянні
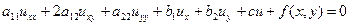
після переходу до змінних ξ, η рівняння, якого б виду воно не було, можна спростити, звільнившись від похідних першого порядку, за допомогою заміни  де
де  - невизначені коефіцієнти, вибираючи які відповідним чином, (щоб знищити 2 коефіцієнти), отримаємо рівняння виду:
- невизначені коефіцієнти, вибираючи які відповідним чином, (щоб знищити 2 коефіцієнти), отримаємо рівняння виду:
 (еліптичне)
(еліптичне)
 (параболічне)
(параболічне)

|
|
|
|
|
Дата добавления: 2017-01-13; Просмотров: 406; Нарушение авторских прав?; Мы поможем в написании вашей работы!