Метод розділення змінних

Розглянемо задачу для скінченої струни.

Спочатку знайдемо розв’язок наступної крайової задачі

Розв’яжемо допоміжну задачу: знайти розв’язок 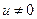такий, що ,

і постає у вигляді .

Підставивши 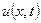у рівняння отримаємо

або

Для і Т отримаємо звичайні диференційні рівняння:

Граничні умови дають 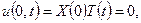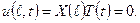Звідки .

Таким чином, для знаходження треба розв’язати задачу про власні значення.

Знайти ті , при яких існує розв’язок задачі:

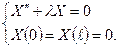
Сформульована задача називається задачею Штурма-Лиувилля.

1. При

, тобто і , отже .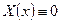

2. При

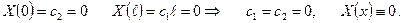
1. При

тобто нетривіальний розв’язок можливий при . Отже при 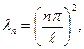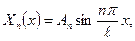де А_п – довільна константа.

Цим же значенням відповідає розв’язок рівняння

, де - довільні коефіцієнти.

Тоді, повертаючись до початкової здачі отримаємо, що функція

- частинні розв’язки рівняння, що задовольняють нульвим граничним умовам.

Для знаходження розв’язку початкової крайової задачі зазначимо, що в силу лінійності рівняння, - задовольняє рівнянню і нульовим граничним умовам, отже

. Знайдемо і враховуючи початкові умови.

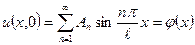
, тобто

.

Зауваження 1. Звісно 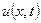є розв’язком коли відповідні ряди для збігаються. В силу властивостей коефіцієнтів Фур’є всі ряди (для ) у загальному випадку сходяться, якщо 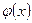має частково-неперервну похідну 3-го порядку, а 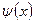має частково-неперервну похідну 2-го порядку і і значить 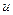– коректно визначений розв’язок, що задовольняє теорему єдиності.

Зауваження 2. 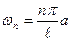- власні частоти коливань струни, або оскільки то (Т – величина натягу, - щільність струни).

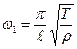- основний тон, решта - обертони. Приведені формули визначають частоту і, відповідно, період основного коливання, пояснюють наступні закони коливання струни, відкриті вперше експериментально (Мерсен)

1. Для струн однакової щільності і однакового натягу період коливання струни пропорційно її довжині.

2. При заданій довжині період змінюється обернено пропорційно кореню квадратному з натягу.

3. При заданій довжині і натягу період змінюється пропорційно кореню квадратному з щільності.

Більш детально про додатки до теорії звуку дивіться [5].

Лекція №14. Перша крайова задача для гіперболічного рівняння

Дата добавления: 2017-01-13