
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Єдиність розв’язку
|
|
|
|
Постанова крайових задач.
Лекція №15. Рівняння параболічного типу
Враховуючи, що параболічне рівняння  описує процес розповсюдження тепла (дифузії) в стержні, то ми отримаємо наступні задачі.
описує процес розповсюдження тепла (дифузії) в стержні, то ми отримаємо наступні задачі.
1. Задача з початковою умовою (у випадку довгого стержня, коли граничні умови не впливають):
знайти розв’язок параболічного рівняння на області  що задовольняє умові
що задовольняє умові  .
.
2. У випадку, коли ділянка, що цікавить, знаходиться поблизу одного з кінців стержня, то розглядають задачу для напівскінченого стержня:
Знайти розв’язок рівняння теплопровідності на області  , що задовольняє умови
, що задовольняє умови

3. У випадку, коли момент часу, що цікавить, достатньо віддалений від початкового, тоді початкова умова не впливає і розглядають задачу без початкової умови:
знайти розв’язок параболічного рівняння на області  , що задовольняє умови:
, що задовольняє умови:

Можна розглядати і інші варіанти.
Перша крайова задача:
Знайти розв’язок  рівняння
рівняння 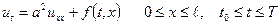 , що задовольняє початковій умові
, що задовольняє початковій умові  , та граничним умовам
, та граничним умовам

де 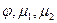 - неперервні і
- неперервні і 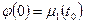
 .
.
По відношенню до кожної з задач виникають запитання:
1) єдиності розв’язку,
2) існування розв’язку.
Ситуація аналогічна випадку з гіперболічним рівнянням.
Теорема. Якщо функція  , визначена і неперервна в замкнутій області
, визначена і неперервна в замкнутій області  і
і  задовольняє рівнянню
задовольняє рівнянню  , то максимальні (мінімальні) значення
, то максимальні (мінімальні) значення  досягаються або в початковий момент, або в точках границі
досягаються або в початковий момент, або в точках границі  .
.
Зауваження: з фізичної точки зору це природно, оскільки немає джерел тепла.
Доведення. Доведемо від супротивного. Нехай 
 , де max обчислюється при
, де max обчислюється при 
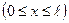 , або при
, або при 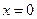 , або при
, або при  , і припустимо що
, і припустимо що  така, що
така, що 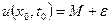 є максимальне значення
є максимальне значення 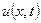 .
.
Порівняємо значення  і
і  в точці
в точці  . Так як функція
. Так як функція  в точці
в точці  досягає свого максимального значення, то
досягає свого максимального значення, то  і
і  .
.
Далі, оскільки  досягає максимуму в точці
досягає максимуму в точці  , то
, то  .
.
Розглянемо функцію  , де
, де  . Очевидно
. Очевидно  і
і  .
.
Виберемо  так, щоб
так, щоб  , тобто
, тобто 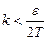 , тоді максимальне значення
, тоді максимальне значення  при
при  , або при
, або при 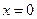 , або
, або  не буде перевищувати
не буде перевищувати 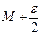 .
.
Однак в силу неперервності  вона повинна в деякій точці
вона повинна в деякій точці  досягати свого максимального значення, тобто
досягати свого максимального значення, тобто  , що
, що  .Враховуючи вище сазане маємо, що
.Враховуючи вище сазане маємо, що  і
і  . По аналогії з вище сказаним
. По аналогії з вище сказаним  і
і

Звідси  .
.
Тобто функція  не задовольняє рівняння в точці
не задовольняє рівняння в точці  що суперечить умові і доводить теорему. Аналогічно доводиться твердження теореми для мінімального значення.
що суперечить умові і доводить теорему. Аналогічно доводиться твердження теореми для мінімального значення.
Теорема (єдиності). Якщо дві функції  і
і  , визначені і неперервні на області
, визначені і неперервні на області  ,
,  , задовольняють рівнянню теплопровідності
, задовольняють рівнянню теплопровідності
 і
і 

 то
то  .
.
Доведення. Розглянемо функцію  , тоді
, тоді  неперервна на області
неперервна на області  ; задовольняє рівняння теплопровідності, а також і нульовим початковому та граничним умовам. Звідси
; задовольняє рівняння теплопровідності, а також і нульовим початковому та граничним умовам. Звідси  , згідно з попередньою теоремою, тобто теорему доведено.
, згідно з попередньою теоремою, тобто теорему доведено.
Використовуючи вище вказаний метод, модифікуючи його під ситуацію, можна показати єдиність розв’язку задачі для нескінченної прямої, дивіться [5].
|
|
|
|
|
Дата добавления: 2017-01-13; Просмотров: 229; Нарушение авторских прав?; Мы поможем в написании вашей работы!