
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Задачі для самостійної роботи. Практичне заняття №11. Параболічні та еліптичні рівняння
|
|
|
|
Задачі.
Практичне заняття №11. Параболічні та еліптичні рівняння
Частинний розв’язок рівняння Лапласа.
Цікавість представляє розв’язок рівняння Лапласа, що володіє циліндричною симетрією (тобто, залежать виключно від  , наприклад при граничних даних, що не залежать від
, наприклад при граничних даних, що не залежать від 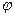 ).
).
Рівняння прийме вигляд 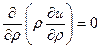 отже
отже 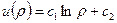 .
.
Приклад. Знайти розподіл тепла на кільці 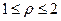 , якщо
, якщо 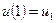
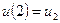 .
.
Розв’язок. Оскільки граничні умови не залежать від 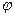 то
то 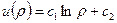 тоді виконуються рівності
тоді виконуються рівності 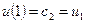 ,
, 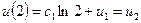 . Отже
. Отже 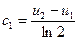 і маємо
і маємо 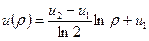 .
.
Необхідні відомості: 1. Розв’язання першої крайової задачі для параболічного рівняння.
2. Розв’язання параболічного рівняння на осі та напівосі. Інтеграл Пуассона.
3. Розв’язок рівняння Лапласа. Інтеграл Пуассона.
1.1 Розв’язати рівняння 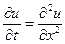 , якщо
, якщо
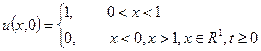 .
.
1.2 Розв’язати 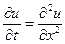 ,
, 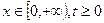 , якщо
, якщо

1.3 Розв’язати 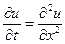
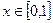 ,
,  , якщо
, якщо
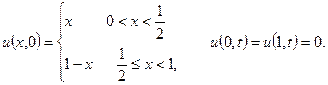
2.1 Знайти стаціонарний розподіл тепла на пластині у формі круга радіуса 1, якщо верхня половина має температуру 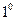 , а нижня
, а нижня 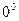 .
.
2.2 Знайти розподіл тепла на кільці 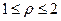 , якщо
, якщо
 .
.
1. Розв’язати 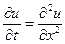 ,
, 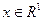 ,
,  , якщо
, якщо
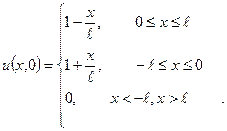
2. Розв’язати рівняння 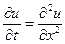 , якщо
, якщо
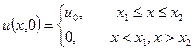 .
.
3. Знайти розподіл тепла для напівскінченного стержня, якщо лівий край х =0 теплоізольовано, а початкова умова: 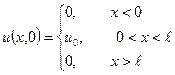 ,
,
(дивіться задачу 2).
4. Розв’язати 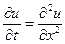
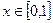 ,
,  , якщо
, якщо 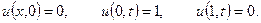
5. Розв’язати 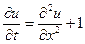
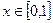 ,
,  , якщо
, якщо 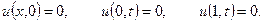
6. Розв’язати 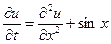
 ,
,  , якщо
, якщо 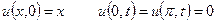 .
.
7. Знайти розподіл тепла на кругу радіуса 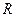 , якщо на граничному колі підтримується температура
, якщо на граничному колі підтримується температура 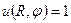
8. Знайти розподіл тепла на кільці 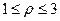 , якщо
, якщо  .
.
9. Знайти стаціонарний розподіл тепла у тонкому стержні з темплоізольованою боковою поверхнею, якщо на кінцях 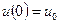 ,
, 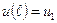 .
.
10. Знайти розв’язок рівняння Лапласа, для внутрішньої частини кільця 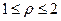 , що задовольняє крайовим умовам
, що задовольняє крайовим умовам

(перейти до полярних координат, та з’ясувати у якому вигляді треба шукати розв’язок).
11. Знайти розв’язок рівняння Лапласа для внутрішньої частини кільця 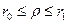 , що задовольняє крайовим умовам
, що задовольняє крайовим умовам
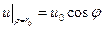 ,
, 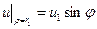 .
.
12. Розв’язати задачу 11 для крайових умов
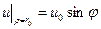 ,
, 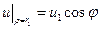 .
.
Література:
1. Понтрячин Л.С Обыкновенные дифференциальные уравнения. – Наука, М., 1970, 331с.
2. Эльсгольш Л.Э Дифференциальные уравнения и вариационное исчисление. – Наука, М., 1969, 423с.
3. Петровский И.Г. Лекции по теории обыкновенных дифференциальных уравнений. – Наука, М., 1970, 279с.
4. Смирнов В.И Курс высшей математики Т2. – Наука, М., 1974, 655с.
5. Тихонов А.Н, Самарский А.А. Уравнения математической физики. – Наука, М., 1972, 735с.
6. Берман Г.Н. Сборник задач по курсу математического анализа. – Наука, М., 1969, 439с.
7. Будак Б.М Самарский А.А, Тихонов А.Н. Сборник задач по математической физике. – Наука, 1972, 687с.
|
|
|
|
|
Дата добавления: 2017-01-13; Просмотров: 251; Нарушение авторских прав?; Мы поможем в написании вашей работы!