
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Формула Даламбера
|
|
|
|
Редукція, загальної задачі.
Лекція №12. Редукція, загальної задачі. Задачі на прямій і напівпрямій. Формула Даламбера, метод продовження
Розв’язок загальної крайової задачі
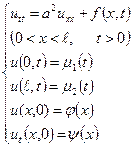
може бути представлено в вигляді
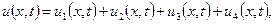
де 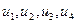 - розв’язок наступних часткових крайових задач:
- розв’язок наступних часткових крайових задач:
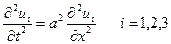
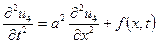
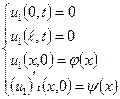
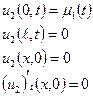
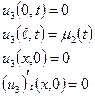
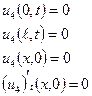 .
.
Аналогічна редукція буде проводитись і для інших крайових задач.
Розглянемо задачу для прямої (безмежної струни) 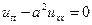
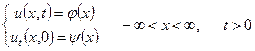 .
.
Рівняння характеристик 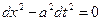 розпадається на рівняння
розпадається на рівняння
 ,
,
інтегруючи які отримаємо  .
.
Зробимо заміну 
Рівняння коливання струни прийме вигляд 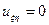 .
.
Тоді для будь якого розв’язку 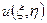 рівняння
рівняння 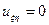 отримаємо
отримаємо 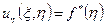 і
і
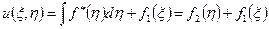 , де
, де 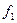 і
і 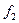 довільні функції.
довільні функції.
Переходячи до змінних 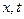 отримаємо
отримаємо
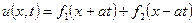 - загальний інтеграл рівняння.
- загальний інтеграл рівняння.
Знайдемо 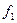 і
і 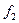 при яких виконуються початкові умови:
при яких виконуються початкові умови:
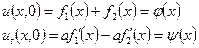 .
.
Із другого рівняння
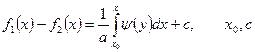 - константи.
- константи.
З рівностей
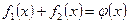
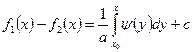
знайдемо
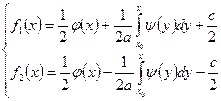 .
.
Підставивши в 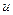 отримаємо
отримаємо
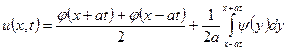 (формула Даламбера).
(формула Даламбера).
Формула Даламбера задовольняє (мається на увазі для двічі диференційованої функці 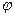 і диференційованої функції
і диференційованої функції 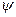 ) рівнянню та початковим умовам. Таким чином, викладений метод доводить як єдиність (будь який розв’язок виражається однією і тою ж формулою), так і існування розв’язку задачі.
) рівнянню та початковим умовам. Таким чином, викладений метод доводить як єдиність (будь який розв’язок виражається однією і тою ж формулою), так і існування розв’язку задачі.
Зауваження. Функція 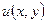 , що визначена за формулою Даламбера, описує процес розповсюдження початкової швидкості. Припустимо що спостерігач знаходиться у момент
, що визначена за формулою Даламбера, описує процес розповсюдження початкової швидкості. Припустимо що спостерігач знаходиться у момент 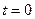 в точці
в точці 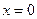 та рухається зі швидкістю
та рухається зі швидкістю 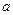 у позитивному напрямку. Впровадимо систему координат, що зв’язана зі спостерігачем,
у позитивному напрямку. Впровадимо систему координат, що зв’язана зі спостерігачем, 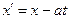 ,
, 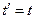 . В цій рухомій системі
. В цій рухомій системі 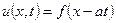 має визначатися формулою
має визначатися формулою 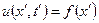 , і спостерігач буде бачити весь час один і той же профіль, що і в початковий момент. Отже,
, і спостерігач буде бачити весь час один і той же профіль, що і в початковий момент. Отже, 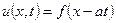 удає незмінний профіль
удає незмінний профіль 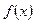 , що поширюється праворуч зі швидкістю
, що поширюється праворуч зі швидкістю 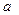 . Функція
. Функція 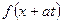 - удає хвилю, що поширюється ліворуч зі швидкістю
- удає хвилю, що поширюється ліворуч зі швидкістю 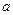 . Таким чином, загальний розв’язок задачі Коші для нескінченної струни є суперпозиція двох хвиль
. Таким чином, загальний розв’язок задачі Коші для нескінченної струни є суперпозиція двох хвиль 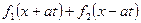 , одна з яких поширюється праворуч, а друга ліворуч зі швидкістю
, одна з яких поширюється праворуч, а друга ліворуч зі швидкістю 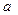 .
.
3. Крайова задача для напівпрямої, і метод продовжень.
Задача. Знайти розв’язок рівняння коливань 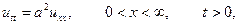
що задовольняє граничній умові 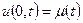 (або
(або 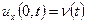 )
)
та початковим умовам 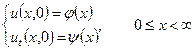 .
.
Розглянемо спочатку ситуацію однорідної граничної умови 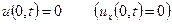 (струна з закріпленим кінцем (або вільним кінцем)).
(струна з закріпленим кінцем (або вільним кінцем)).
Для рівняння коливань на безмежній прямій справедлива лема (із формули Даламбера)
Лема. Якщо початкові дані в задачі про поширення коливань на необмеженій прямій являються непарними (парними) функціями відносно деякої точки х 0, то відповідний розв’язок (похідна по х розв’язку) в цій точці х 0 дорівнює 0.
За допомогою леми розв’яжемо задачу:
знайти розв’язок рівняння 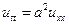 , що задовольняє початковим умовам
, що задовольняє початковим умовам

і граничній умові 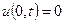 .
.
Розглянемо функції Φ(х), Ψ(х) – що являються непарним продовженням 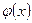 і
і 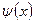 :
:
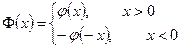
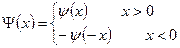 .
.
Функція
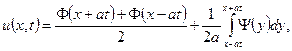
в силу леми, задовольняє рівностям 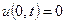 ,
,
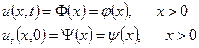 .
.
Розглядаючи отриману функцію 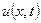 тільки для
тільки для 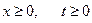 отримаємо функцію, що задовольняє усім умовам поставленої задачі.
отримаємо функцію, що задовольняє усім умовам поставленої задачі.
Повертаючись до функцій 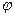 і
і  можемо написати
можемо написати
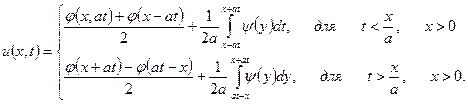
Аналогічно розглядається ситуація з вільним кінцем 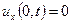 (в цьому випадку
(в цьому випадку 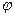 і
і 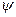 продовжують парним чином). Розглянути самостійно.
продовжують парним чином). Розглянути самостійно.
Розглянемо розв’язок рівняння при нульових початкових і довільній граничній умовах:
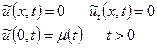 .
.
Граничний режим викликає хвилю, що поширюється впродовж струни зі швидкістю 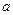 , тобто розв’язок має вигляд:
, тобто розв’язок має вигляд:
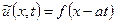 .
.
Визначимо 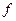 з умови
з умови
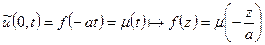 ,
,
так, що 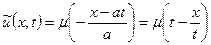 .
.
Але ця функція визначена лише в області 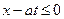 , так як
, так як 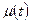 визначена для
визначена для 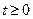 . Щоб знайти
. Щоб знайти 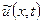 для всіх аргументів продовжимо
для всіх аргументів продовжимо 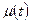 на
на 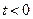 поклавши
поклавши 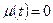 ,
, 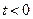 . Тоді
. Тоді 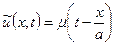 задана для всіх аргументів і задовольняє нульовим початковим умовам.
задана для всіх аргументів і задовольняє нульовим початковим умовам.
Розв’язок 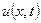 задачі:
задачі:
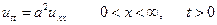
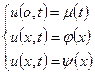
представляється у вигляді суми розв’язків попередньої задачі та 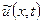 і має вигляд
і має вигляд
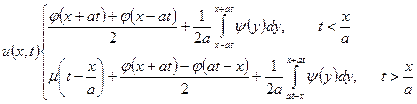 .
.
|
|
|
|
|
Дата добавления: 2017-01-13; Просмотров: 838; Нарушение авторских прав?; Мы поможем в написании вашей работы!