
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Тема 10. Решение системы двух уравнений с двумя переменными
|
|
|
|
| Теория | Практика |
Решить систему уравнений – значит найти множество её решений.
Решением системы двух уравнений с двумя переменными является пара значений переменных, обращающая каждое уравнение системы в верное числовое равенство.
Системы уравнений с двумя переменными можно решать: а) графическим способом;
б) способом подстановки;
в) способом сложения (вычитания).
Выбор способа решения зависит от уравнений, входящих в систему.
Графический способ применим к решению любой системы, но с помощью графиков уравнений можно приближенно находить решения системы. Лишь некоторые найденные решения системы могут оказаться точными. В этом можно убедиться, подставив их координаты в уравнения системы.
Способ подстановки «хорош» при решении систем, когда одно из уравнений является уравнением первой степени. Полезно помнить алгоритм решения этим способом:
1.Из уравнения первой степени выражают одну переменную через другую.
2.Подставляют полученное выражение в уравнение второй степени
3.Решают получившееся уравнение.
4. Находят соответствующие значения второй переменной.
Способом сложения лучше пользоваться в случае, когда оба уравнения системы есть уравнения второй степени.
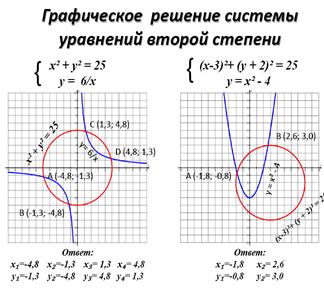
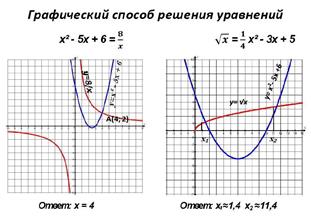
| 1. Решим систему уравнений
 Решение: Выразим из второго уравнения переменную x через y:
Решение: Выразим из второго уравнения переменную x через y:  .
Подставим в первое уравнение вместо x выражение .
Подставим в первое уравнение вместо x выражение 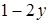 , получим уравнение с переменной y: , получим уравнение с переменной y:
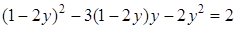 .
После упрощения получим равносильное уравнение .
После упрощения получим равносильное уравнение
 .
Решив его, найдем, что .
Решив его, найдем, что  , ,  . Подставив в формулу . Подставив в формулу   , получим: , получим:  .
Подставив в формулу .
Подставив в формулу  ; ;  , получим: , получим:
 .;Итак система имеет два решения: .;Итак система имеет два решения:
 , ,  и и  , ,  . Ответ можно записать также в виде пар: . Ответ можно записать также в виде пар:  , ,  .
Если система состоит из двух уравнений второй степени с двумя переменными, то найти ее решения обычно бывает трудно. В отдельных случаях такие системы удается решить, используя способ подстановки или способ сложения.
2. Решим систему уравнений .
Если система состоит из двух уравнений второй степени с двумя переменными, то найти ее решения обычно бывает трудно. В отдельных случаях такие системы удается решить, используя способ подстановки или способ сложения.
2. Решим систему уравнений
 Решение: Т.К.
Решение: Т.К.  , выразим из второго уравнения переменную y через x: , выразим из второго уравнения переменную y через x:  .; Подставим в первое уравнение вместо y выражение .; Подставим в первое уравнение вместо y выражение  .
Получим уравнение относительно x: .
Получим уравнение относительно x:  . .  , ,  .
По формуле .
По формуле  находим y: находим y:
 , ,  .
Значит, система имеет два решения: .
Значит, система имеет два решения:
 , ,  и и  , ,  .
Ответ: .
Ответ:  , ,  .
3. Вычислите координаты точки В.
Решение. Точка В является пересечением прямых .
3. Вычислите координаты точки В.
Решение. Точка В является пересечением прямых 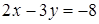 и и  . Решив систему . Решив систему  , найдем, что , найдем, что 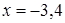 ; ; 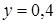 .
Ответ: В (-3,4;0,4).
4. Решите систему уравнений .
Ответ: В (-3,4;0,4).
4. Решите систему уравнений 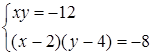 .
Решение. Преобразуем второе уравнение системы .
Решение. Преобразуем второе уравнение системы  к виду к виду  . Подставим в него . Подставим в него  . Выполнив преобразования, получим систему: . Выполнив преобразования, получим систему:
 .
Решив эту систему, получим: (-2;6), (3;-4).
Ответ: (-2;6), (3;-4). Возможна запись ответа в другом виде: .
Решив эту систему, получим: (-2;6), (3;-4).
Ответ: (-2;6), (3;-4). Возможна запись ответа в другом виде:  , , 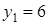 , ,  , ,  , или , или  и и  .
Другое возможное решение. Выразим из первого уравнения одну из переменных через другую, например, .
Другое возможное решение. Выразим из первого уравнения одну из переменных через другую, например,  . Подставим . Подставим  во второе уравнение системы, получим уравнение во второе уравнение системы, получим уравнение 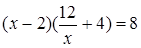 . После преобразований получим квадратное уравнение . После преобразований получим квадратное уравнение  .
Найдем корни данного уравнения и соответствующие значения y, получим: (-2;6), (3;-4). .
Найдем корни данного уравнения и соответствующие значения y, получим: (-2;6), (3;-4).
|
Тема 11 Составление уравнения по условию текстовой задачи
| Теория | Практика |
Решение сложных задачцелесообразно начать с повторения алгоритмарешения системы уравнений с 2-мя неизвестными:
-Обозначить неизвестную величину переменной (при решении задачи с помощью системы уравнения вводят несколько переменных);
-Выразить через нее другие величины;
-Составить уравнение (или систему уравнений), показывающее зависимость неизвестной величины от других величин;
-Решить уравнение (или систему уравнений);
-Сделать проверку при необходимости;
-Выбрать из решений (или систему уравнений) те которые подходят по смыслу задачи;
-Оформить ответ.
2. Задачи на движение по реке. При решении задач на движение по реке необходимо учесть, что
 , ,  где: где:
 – скорость по течению реки; – скорость по течению реки;
 – скорость объекта при движении против течения реки; – скорость объекта при движении против течения реки;
 – собственная скорость движущегося объекта; – собственная скорость движущегося объекта;
 – скорость течения реки. – скорость течения реки.
| 1. Расстояние между двумя причалами по реке 14 км. На путь против течения реки лодка затратила на 1 ч больше, чем на обратный путь по течению. Найдите собственную скорость лодки, если скорость течения реки 2 км/ч.
Обозначьте буквой х собственную скорость лодки (в км/ч) и составьте уравнение по условию задачи.
1)  2) 2)  3)
3) 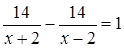 4) 4)  Решение. x (км/ч) — собственная скорость лодки, тогда
Решение. x (км/ч) — собственная скорость лодки, тогда  (км/ч) — скорость по течению, (км/ч) — скорость по течению,  (км/ч) — скорость против течения.
Расстояние между причалами 14 км, следовательно, (км/ч) — скорость против течения.
Расстояние между причалами 14 км, следовательно,
 (ч) — время движения лодки по течению; (ч) — время движения лодки по течению;
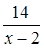 (ч) — время движения лодки против течения.
Время движения лодки против течения больше, чем по течению, на 1 час, поэтому составим уравнение: (ч) — время движения лодки против течения.
Время движения лодки против течения больше, чем по течению, на 1 час, поэтому составим уравнение:  .
Ответ: 2.
2. Прочитайте задачу: «От турбазы до станции турист доехал на велосипеде за 5 ч. На мопеде он мог бы проехать это расстояние за 3 ч. Известно, что на мопеде он едет со скоростью на 8 км/ч больше, чем на велосипеде. Чему равно расстояние от турбазы до станции?»
Выберите уравнение, соответствующее условию задачи, если буквой х обозначено расстояние (в км) от турбазы до станции.
1) .
Ответ: 2.
2. Прочитайте задачу: «От турбазы до станции турист доехал на велосипеде за 5 ч. На мопеде он мог бы проехать это расстояние за 3 ч. Известно, что на мопеде он едет со скоростью на 8 км/ч больше, чем на велосипеде. Чему равно расстояние от турбазы до станции?»
Выберите уравнение, соответствующее условию задачи, если буквой х обозначено расстояние (в км) от турбазы до станции.
1)  3) 3)  2)
2)  4) 4)  Решение. Пусть х км — расстояние от турбазы до станции. Тогда
Решение. Пусть х км — расстояние от турбазы до станции. Тогда  км/ч — скорость, с которой турист едет на велосипеде; км/ч — скорость, с которой турист едет на велосипеде;  км/ч — скорость, с которой турист едет на мопеде. Известно, что скорость на мопеде на 8 км/ч больше скорости на велосипеде: запишем уравнение км/ч — скорость, с которой турист едет на мопеде. Известно, что скорость на мопеде на 8 км/ч больше скорости на велосипеде: запишем уравнение  .
Уравнение может быть записано и в другом виде, например, .
Уравнение может быть записано и в другом виде, например, 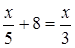 , но его легко преобразовать к виду: , но его легко преобразовать к виду:  .
Ответ: 3. .
Ответ: 3.
|
|
|
|
|
|
Дата добавления: 2017-01-13; Просмотров: 744; Нарушение авторских прав?; Мы поможем в написании вашей работы!