
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Тема 18 Решение линейного неравенства с одной переменной с использованием сравнения квадратного корня с рациональным числом
|
|
|
|
На множители
Тема 17. Решение уравнения третьей степени разложением
| Теория | Практика |
Чтобы разложить многочлен на множители нужно сгруппировать члены многочлена так, чтобы группы имели одинаковый общий множитель, записать сумму группировок и вынести общий множитель за скобки в каждой группе
  x2+3x-4x-12=0
(x2+3x)+(-4x-12)=0
x(x+3)-4(x+3)=0
(x+3)(x-4)=0
x +3=0 или x-4=0
x=-3 x=4
Ответ: -3; 4 x=-3 x2+3x-4x-12=0
(x2+3x)+(-4x-12)=0
x(x+3)-4(x+3)=0
(x+3)(x-4)=0
x +3=0 или x-4=0
x=-3 x=4
Ответ: -3; 4 x=-3
| 1. Решите уравнение: 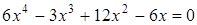 Решение.
Решение. 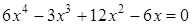
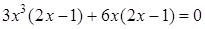
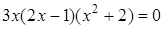
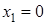 , , 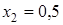 Ответ: 0; 0,5.
2. Решите уравнение:
Ответ: 0; 0,5.
2. Решите уравнение: 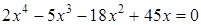 Решение:
Решение: 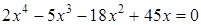
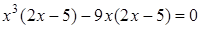
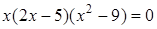
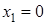 , , 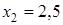 , , 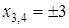 .
Ответ: 0; 2,5; -3; 3.
3. Сократите дробь .
Ответ: 0; 2,5; -3; 3.
3. Сократите дробь 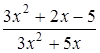 .
Решение. Корни квадратного трехчлена .
Решение. Корни квадратного трехчлена 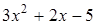 : :  , , 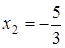 . Имеем: . Имеем: 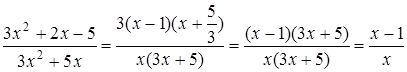 .
Замечание. Можно разложить трехчлен на множители способом группировки: .
Замечание. Можно разложить трехчлен на множители способом группировки:
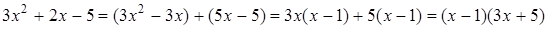 Ответ: Ответ: 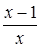 .
4. (Демо 2010, Задание 17) Решите уравнение .
4. (Демо 2010, Задание 17) Решите уравнение
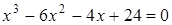 .
Решение. Разложим на множители левую часть уравнения. Получим: .
Решение. Разложим на множители левую часть уравнения. Получим: 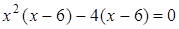 , , 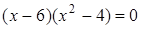 , , 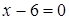 или или 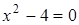 . Значит, уравнение имеет корни: -2; 2; 6.
Ответ: -2; 2; 6. . Значит, уравнение имеет корни: -2; 2; 6.
Ответ: -2; 2; 6.
|
Реши сам:
1. Найдите произведение корней уравнения 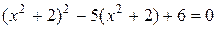 .
.
2. Решите уравнение 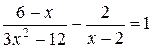 .
.
3. Найдите наибольший корень уравнения 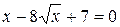 .
.
4. Докажите, что уравнение 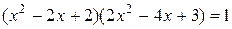 имеет корень равный 1, а других корней у него нет.
имеет корень равный 1, а других корней у него нет.
5. Найдите произведение корней уравнения  .
.
6. Решите уравнение 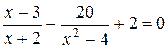 .
.
7. Найдите наименьший корень уравнения 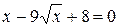 .
.
8. Докажите, что уравнение 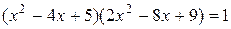 имеет корень равный 2, а других корней у него нет.
имеет корень равный 2, а других корней у него нет.
9. Найдите произведение корней уравнения 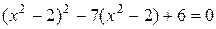 .
.
10. Решите уравнение 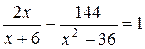 .
.
11. Найдите наибольший корень уравнения 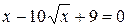 .
.
12. Докажите, что уравнение 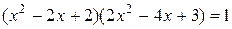 имеет корень равный 1, а других корней у него нет.
имеет корень равный 1, а других корней у него нет.
13. Разложите на множители: 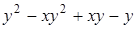 .
.
14. Решите уравнение  .
.
| Модель 1 Баллы | Критерии оценки выполнения задания |
| Ход решения верный, оба его шага выполнены, получен верный ответ. | |
| Ход решения правильный, многочлен в левой части уравнения разложен на множители, но при этом допущена ошибка в знаке, например, получен двучлен, ответ дан с учетом этой ошибки. 24 x + Или: допущена описка на последнем шаге. | |
| Другие случаи, не соответствующие указанным критериям. | |
| Модель 2 Баллы | Критерии оценки выполнения задания |
| Ход решения верный, оба его шага выполнены, получен верный ответ. | |
| Ход решения правильный, многочлен в левой части уравнения разложен на множители, но при этом допущена ошибка в знаке, например, получен двучлен, ответ дан с учетом этой ошибки. Или: допущена описка на последнем шаге. 24x+ | |
| Другие случаи, не соответствующие указанным критериям. |
| Теория | Практика |
| Полезно повторить: 1. Теоретический материал темы 13 и 14. 2. Метод интервалов для решения неравенст. 3.Сравнение квадратного корня с рациональным числом: | 1. Решите неравенство  Решение. Умножим обе части неравенства
Решение. Умножим обе части неравенства  на 20, получим неравенство на 20, получим неравенство 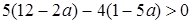 . Решив его, получим . Решив его, получим 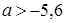 . Наименьшее целое значение а, удовлетворяющее этому неравенству, равно -5.
Ответ: -5.
2. Решите неравенство . Наименьшее целое значение а, удовлетворяющее этому неравенству, равно -5.
Ответ: -5.
2. Решите неравенство 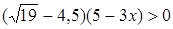 .
Решение: 1) Определим знак разности .
Решение: 1) Определим знак разности 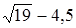 . Так как . Так как 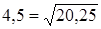 и и 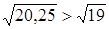 , то , то  .
2) Получаем неравенство .
2) Получаем неравенство  . Отсюда . Отсюда 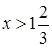 .
Ответ: .
Ответ: 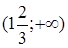 . Другая возможная форма ответа: . Другая возможная форма ответа: 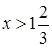
|
|
|
|
|
|
Дата добавления: 2017-01-13; Просмотров: 668; Нарушение авторских прав?; Мы поможем в написании вашей работы!