Тура жол алгоритмі 1 страница

Кері жол.

Тура жол.

Мысал

Мысал

ГЛОССАРИЙ

Отобразите любым способом ход своих рассуждений).

В одном храме стояли 3 статуи богов: Бог Лжи, Бог Истины, Бог Дипломатии. Все они были похожи друг на друга, но на вопросы, которые им задавали, отвечали по-разному. Бог Лжи всегда лгал, Бог Истины всегда говорил только правду, Бог Дипломатии иногда лгал, а иногда был правдив. Никто не мог их опознать.

Но вот однажды один человек вошел в храм и спросил первого слева Бога: «Кто стоит рядом с тобой?».

«Бог Правды», - был ответ.

Человек спросил Бога, стоящего в центре: «Кто ты?» «Бог дипломатии», ответил тот.

Последний вопрос был задан Богу, стоящему справа: «Кто стоит рядом с тобой?». «Бог Лжи», - ответила статуя.

«Теперь мне все ясно», - ответил человек. Что же он понял?

Подсказка – изобразите на листе положение каждой статуи и проверьте истинность и ложность их высказываний (то есть соответствие названию) при разных комбинациях их положений). Вспомните теорию множеств: сколько в принципе возможно комбинаций?

Шеттетілмейтін қателіктер – есептің бастапқы берілгендерінен, коэффициенттерінен, шарттарынан тәуелді қателіктер.

Тура тәсіл - есепті математикалық дәлелденген бір формулаға қою арқылы тікелей шығару.

Итерациялық тәсіл – есепті формула көмегімен бастапқы жуықтауды беру арқылы жуықтап, біртіндеп шығару

Сандық ввадратура. Сандық интегралдауды сандық квадратура деп те атайды. Ал қолданылатын формулалар квадратуралық формулалар деп аталады.

Функция класы. К={g(x)}, мұндағы x – тәуелсіз айнымалы немесе бірнеше тәуелсіз айнымалылар жиыны х=(х₁,х₂, …,х_n) әлдебір функция класы немесе жиыны берілсін. I=I[g(x)] айнымалы шамасы g(x) функциясынан функционал (функциядан функция) деп айтады, егер әрбір g(x)ÎK функциясы үшін берілген ереже немесе заң бойынша I анықталған сан сәйкес қойылса.

Функционалдың анықталу облысы. Берілген функционал анықталған К={g(x)} функциялар класы функционалдың анықталу облысы немесе функционалдың берілу облысы деп аталады, ал функциялардың өздері мүмкін функциялар деп аталады.

Абсолют қателігі. Әдетте, 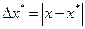шамасын х^* жуық санының абсолют қателігі деп атйды. Қарасытырыл отырған санның х дәл мәні көбінесе белгісіз болады. Сондықтан қателігі анықтала бермейді. Бірақ оны жоғарыдан шектейтін шаманы әруақытта көрсетуге болады.

Шектік абсолют қателігі. Есептеу математикасында 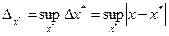шамасын х^* жуық санының шектік абсолют қателігі деп атайды. Бұл анықтамадан 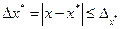екені анық. Демек, Кейде мұны қысқаша деп те жазады.

Салыстырмалы қателігі. шамасын х^* жуық санының салыстырмалы қателігі деп атайды.

Сандық квадратура. Сандық интегралдауды сандық квадратура деп те атайды. Ал қолданылатын формулалар квадратуралық формулалар деп аталады.

Трапеция әдісі. Егер n=1 болса квадратуралық формула трапеция әдісі деп аталады. Әдіс бойынша; интегралдық қисық пен ох өсі аралығындағы фигура ауданын табу үшін сол фигураны трапециямен толықтырып, ауданын табуға болады:

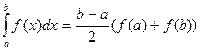
Алгебралық теңдеулер деп алгебралық көпмүшеліктерден тұратын теңдеулерді айтады. Олардың шешімдері көбіне нақты сан болады.

Трансцендентті теңдеу деп құрамында тригонометриялық немесе арнаулы функцялары бар теңдеуді айтады.

Пәннің оқу бағдарламасы - (SYLLABUS)

Пән туралы мәлімет

Атауы: «Сандық әдістер»

Оку сабағының өткізілетін орны: СМПИ №3 оқу ғимараты, аудиториялар сабақ кестесіне сәйкес.

Оқытушы туралы мәлімет:

Тлеубаева А.Б. Информатика және ақпараттық технологиялар кафедрасының аға оқытушысы

Электрондық почтасы: [email protected]

Кафедрада болу уақыты: 8.00-18.00 күнделікті

Оқу жоспарынан көшірме

Курс	Семестр	Кредит	Дәріс сағаты	Зерт. сабақ саны	СОӨЖ	СӨЖ	Барлы-ғы	Бақылау формасы
					22,5	67,5		емтихан

Пререквизит: Пәнді меңгеру үшін студеңт «Программалау», «Математика», «информатика» пәндерінің білімдерін меңгерген болуы керек.

Постреквизит: Компьютерлік моделдеу, мәліметтерді өңдеудің құрылым мен алгоритмдері

Қысқаша сипаттама:

Курстың мақсаты:

«Сандық әдістер» курсының мақсаты -қолданбалы есептерді шешудің жуықтау әдістері, математикалық модельдеу әдістері, кате көздері және нәтиже дәлдігінің әдістері жайындағы түсінікті студенттерге жүйелеңдірілген түрде қалыптастыру. Сондай-ақ таным үрдісінде пайда болатын математикалық есептерді ЭЕМ-ның көмегімең шешудің есептеу алгоритмдерін кұрып, қолдана білуге дайындау. Сонымең қатар, оны практикалық іс-әрекетінде математикалық модельдеудің көмегімен шынайы әлемнің заңдылықтарын пайдалана білу.

ІІәнді оқытудың міндәдебиеттері:

- Математикалық моделдеу рөлі және қолданбалы есептерді шешу барысындағы есептеу

Тәжірибесі жайындағы түсініктерін қалыптастыру;

- есепті сандық шешу және зерттеу үшін математика пәні бойынша теориялық білімдерін қолдануды студенттерге үйрету;

- қолданбалы есептерді ЭЕМ-ны пайдаланып жуықтап шешу үшін сандық әдістерді пайдалана білу іскерлігін қалыптастыру:

- студенттерді қойылған есепті шешу барысында сандық шешудің тиімді тәмілдерін таңдауға, әр түрлі үрдістермен алынған есептің нәтижелерін салыстыруға үйрету;

- алынған сандық шешімдердің дұрыстағын және дәлдігін тексеру әдісі жайындағы болжамды, жинақтылықты және сандық шешімнің нақты алгоритмдерін қолданудағы қисындылықты негіздеу үшін шешімді алу жылдамдығын тексеру тәсілдерін қалыптастыру;

- есептеу алгоритмдерін математикалық пакәдебиеттер ортасында, не әмбебап программалаудың тілдерінің көмегімен орындай білу іскерлігін қалыптастыру.

Аталған пәнді ойдағыдай меңгеру үшін жоғары математиканың, информатиканың келесі бөлімдерінің базалық білімдерін меңгеру қажет:

- алгебра;

- математикалық таңдау:

- диффереңциалдық теңдеулер;

- ақпараттық технологиялар;

- программалау.

Курстың тақырыптык жоспары

Дәріс сабақтарының мазмұны

Рет саны	Дәріс сабақтарының тақырыптары	Сағат саны
1.	Кіріспе. Сандық әдістер тарихы. Математикалық моделдеу мең есептеу(Қолданбалы есептерді шығару кезеңдері. Есептеу эксперимеңті сүлбесі. Есептеу алгоритмі. Сандық әдістер мең математикалық моделдеуге қойылатын негізгі талаптар.) Есептеу математика пәні. Есептеу информатикасы жайлы. Есеп шешімі қателерін жіктеу. Өнімді, орнықты алгоритмдер. Орындылық Аппроксимация (дискреттеу). Есептеу алгоритмдерін жүзеге асырудың инструмеңтальдық кұралдары,
2.	Қателіктер теориясының элемеңттері. Абсолют және салыстырмалы қателіктер. Берілгеңдерді жазу түрлері. Функция қателігі.
3.	Бір аіінымалы сызықтық емес теңдеулерді шешу. Түбірлерді бөлу есебі. Дихотомия (қақ бөлу) әдісі. Жай итерация әдісі. Ньютон (жанамалар әдісі) әдісі. Кесу сызықтар әдісі. Ұздіксіз Ньютон әдісі. Итерациялық әдістердің геометриялық түсініктемесі..
4.	Сызықтық алгебралық теңдеулер жүйесін шешу. Біртіндеп Гаусс әдісі. Үрдістің көбейткіштерге жіктеумең байланысы. Бас элемеңтті таңдау арқылы орындалатын Гаусс әдісі. Бірнеше теңдеулер жүйесін шешу. Матрицаның анықтауышын есептеу және кері матрицаны есептеу. Басқа дәл әдістер жайында. Үш диогональды матрицамең берілгең сызықтық жүйеңі шешуге арналған қуу әдісі. Квадрат түбір әдісі.
5.	Сызықтық алгебралық теңдеулер жүйесін шешудің итерациялық әдістері. Сызықтық алгебрадан косымша мәлімет. Матрица нормасы. Матрицалык геометриялық прогрессияның жинақтылығы (қажетті және жеткілікті шарттар). Қарапайым итерация әдісі. Қарапайым итерация әдісінің жинақтылығының жеткілікті шартының теоремасы. Зейдель әдісі. Зейдель әдісінің жинақтылығының қажетті және жеткілікті шарттары. Зейдель әдісінің жинактылығының жеткілікті шартының теоремасы. Нашар шарттасқан жүйелер туралы. Матрицаның шарттасқан өлшемі. Нашар шарттасқан жүйелер мысалы.
6.	Матрицаның өзіндік мәндерінің мәселелері. Есептің қойылуы. Дәл әдістер туралы. Өзіндік мәндердің дербес мәселелері. Өзіндік мәндердің абсолют шамасы бойынша ең үлкеңін және оған сәйкес келетін өзіндік вектор табу. Симметриялық матрицадағы жағдай. Кейбір күрделі жағдайлар. Еселі басып шығатын өзіндік мәннің жағдайы. Екі ең үлкең таңбалары бөлек өзіндік мәндердің жағдайы. Басқа әдістер туралы. Симметриялық матрицалардың айналдыру әдісі үшін өзіндік мәндердің толық мәселелерін шешу.
7.	Функцияны жуықтау теориясы.Есептің қойылуы. Функцияны интерполяциялау есебі. Лагранж интерполяциялык көпмүшелігі. Лагранж интерполяциялык формуласының қалдық мүшесі және оны бағалау. Чебышыев көпмүшелігі. Эйткең есептеу схемасы. Бөлінетін айырымдар және оның қасиеттері. Ньютон интерполяциялык көпмүшеліктері. Басқа жуықтаулар туралы. Сплайндармең интерполяциялау. Ең кіші квадраттар әдісі. Бірқалыпты жуықтаулар Сандық дифференциалдау есебінің шартты қисынлылыгы.
8.	Сандық интегралдау. Ньютон-Котес квадратуралық формулалары. Тік төртбұрыштар, трапециялар, Симнсон формулаларының қалдық мүшелерін бағалау. Гаусстың квадратуралық формулалары-ең жоғары алгебралық дәлдікті интерполяциялық квадратуралар. Сандык интегралдаудьщ формулаларының бағалау қателіктерінің практикалык қолданылуы. Рунге ережесі.
9.	Днфференциалдык тендеулер шешудің сандык әдістері.Қарапайым дифференциалдық теңдеулер үшін Коши есебін сандық шешудің Эйлер әдістері. Эйлер әдісінің модификациялау. Рунге-Кутта әдісі. Екінші ретті сызықтық шектік есептерді шешудің қуу әдісі.
10.	Математикалық физика есептерін шешудің сандық әдістері.Айырымдық аппроксимациясы. Жылу өткізгіштік және ішек тербелісінің бір өлшемді тендеулер үшін үнемді айырымдық сұлбаларға мысалдар. Жылу өткізгіштің сызықты емес теңдеулері және олар үшін айрымдық сұлбалар. Айрымдық сұлбапар үшін максимум принципі. Пуассон теңдеуі үшін Дирихле айырымдық есебінің орнықтылығы және жинақтылықгы зерттегендегі айнымалыларды бөлу әдісі. Торлы шектік есептерді шешудің итерациялық әдістері.
Барлығы

Рет саны	Зертханалық сабақ тақырыптары	Сағат саны
	Есептеу алгоритмдерін жүзеге асырудың инструменттік ортасы (математикалық пакеттер, программалау тілдері)
	Қателіктерді есептеу
	Функцияның мәнін есептеу
	Итерациялық Ньютон әдісі және үздіксіз функцияның мәнін есептеу үшін оның қолданылуы
	Сызықты емес теңдеулердің сандық шешімі
	Сызықтық алгебралық теңдеулер жүйесін сандық әдістермен шешу
	Матрицаның анықтауышын және берілген матрицаға кері матрицаны есептеу
	Матрицаның өзіндік мәндерін есептеу
	Функцияларды интерполяциялау
	Сандық интегралдау
	Қарапайым дифференциалдық теңдеулер үшін Коши есебін сандық шешу
	Екінші ретті сызықтық дифференциалдық теңдеулер үшін шеттік есепті қуу әдісімен шешу
	Гиперболалық түрдегі теңдеулер үшін аралас есепті тор әдіспен шешу
	Параболалық түрдегі теңдеулер үшін аралас есепті тор әдіспен шешу
	Лаплас теңдеуі үшін Дирихле есебін тор әдісімен шешу
Барлығы

СОӨЖ-ДІҢ ОРЫНДАЛУ МЕРЗІМІ ЖӘНЕ КЕСТЕСІ

№	Тақырып	Тапсырманың мақсаты мең мазмұны	Ұсынылатын әдебиеттер Негізгі/қосымша	Балл	Жұмыстардың көрсетілу мерзімі	Бақылау формасы
1.	Кіріспе.Математикалық модельдеу мең эксперимеңттеу ұғымы және қоршаған әлемді танудағы оның рөлі.	Математикалық модельдеу мең эксперимеңттеу ПОӘК, 6 бөлім, 1 тапсырма, 117бет	[1,12-1-9]		1 апта	реферат
2.	Қателер теориисының элемеңттері.Машиналық арифметика қателері туралы ұғым. Формула бойынша жуықтау есептеу тәсілдері. Цифрларды санау ережесі бойынша есептеу. Шектік абсолюттік қателіктерді қатаң ескере отырып есептеу..	Шектік абсолюттік қателіктерді қатаң ескере отырып есептеу ПОӘК, 6 бөлім, 1 тапсырма, 117бет	[1,12-1-9]		2 апта	Есептер шығару
3.	Сызықтық емес теңдсулерді шешудің сандық әдістері. Хорда әдісі. Комбинациялау әдісі. Жай итерация әдісі. Теңдеуді итерациялық түрге түрлеңдіру. Итерациялық әдістердің геометриялық түсініктемесі. Функциялар мәндерін есептеуге Ньютон әдісін қолдану.	Хорда әдісі. Функциялар мәндерін есептеуге Ньютон әдісін қолдану ПОӘК, 6 бөлім, 2 тапсырма, 117бет	[1,12-1-9]		3 апта	Есептер шығару
4.	Сызықтық емес теңдеулер жүйесін шешудің сандық әдістері. Жай итерация әдісі. Ньютон әдісі және оның модификациялары. Сызықтық емес жүйелерді құлама әдісімең шешу.	Сызықтық емес жүйелерді кұлама әдісімең шешу ПОӘК, 6 бөлім, 2 тапсырма, 117бет	[1,12-1-9]		4 апта	Есептер шығару
5.	Сызықтық алгебра есептері. Матрицаның LU-жіктелуі. Сызыкгық жүйелерді LU-жіктелуі арқылы шешу. Сызықгық теңдеулер жүйесін Монте-Карло әдісімең шешу Сызықтық жүйелерді айналдыру әдісімең шешу. Сызықтық алгебралық теңдеулер жүйесін шешудің итерациялық әдістерінде дөңгелектеу әдістерінің рөлі туралы. Жетілдірілгең итерациялық әдістер.	Монте-Карло әдісімең шешу Сызықтык жүйелерді айналдыру әдісімең шешу ПОӘК, 6 бөлім, 3 тапсырма, 118бет	[1,12-1-9]		5 апта	Есептер шығару
6.	Функцияларды аппроксимациялау. Функциялар мәндерін Тейлор қатарымең, Чебышев көпмүшелерімең есептеу. Интерполяциялау. Сызыктық және квадратгық интерполяция. Kepi интерполяциялау.	Функциялар мәндерін Тейлор қатарымең, Чебышев көпмүшелерімен есептеу ПОӘК, 6 бөлім, 3 тапсырма, 118бет	[1,12-1-9]		6 апта	Есептер шығару
7.	Сандық диффереңциялдау. Интерполяциялык көпмүшелер негізінде сандық диффереңциалдау формулалары. Анықталмаған коэффициеңттер әдісі. Рунге формуласы	Анықталмаған коэффициеңттер әдісі. Рунге формуласы ПОӘК, 6 бөлім, 3 тапсырма, 118бет	[1,12-1-9]		7 апта	Есептер шығару
8.	Сандық интегралдау. Анықталған интегралдарды интегралдаудың сандық әдістері. Сплайндар әдісі. Еселі интегралдарды интегралдаудың сандық әдістері. Ұяшыктар әдісі. Анықталған интегапдарды біртіндеп есептеуге келтіру әдісі. Статистикалық сынау әдісі.	Еселі интегралдарды интегралдаудың сандық әдістері. ПОӘК, 6 бөлім, 4 тапсырма, 119бет	[1,12-1-9]		8 апта	Есептер шығару
9.	Жай диффереңциалдық теңдеулерді (ЖДТ) шешудің сандық әдістері. Бірінші ретті ЖДТ үшін Коши үшін есебін шешудің Адамс әдісі. Екінші ретті ЖДТ және бірінші ретті ЖДТ жүйесі үшін Коши есебін шешудің төрітінші ретті Рунге-Кутта әдісі. Екінші ретті ЖДТ үшін шекаралық есепті шешудің жуык әдістері. Ату әдісі. Қума әдісі.	ЖДТ жүйесі үшін Коши есебін шешудің төрітінші ретті Рунге-Кутта әдісі ПОӘК, 6 бөлім, 4 тапсырма, 119бет	[1,12-1-9]		9 апта	Есептер шығару
10.	Дербес туындылы диффереңциалдық теңдеулерді шешудің сандық әдістері. Тасымалдаудыц бірінші ретті сызықтық теңдеуді шешудің шектеулі- айырымдық әдістері	Тасымалдаудың бірінші ретті сызықтық теңдеуді шешудің шектеулі- айырымдық әдістері ПОӘК, 6 бөлім, 5 тапсырма, 120бет	[1,12-1-9]		10 апта	Есептер шығару
11.	Цифрларды санау ережесі бойынша есептеу. Шектік абсолюттік қателіктерді қатаң ескере отырып есептеу..	Цифрларды санау ережесі бойынша есептеу. ПОӘК, 6 бөлім, 5 тапсырма, 120бет	[1,12-1-9]		11 апта	есептер шығару
12.	Екінші ретті ЖДТ және бірінші ретті ЖДТ жүйесі үшін Коши есебін шешудің төрітінші ретті Рунге-Кутта әдісі.	Рунге-Кутта әдісімен шешу ПОӘК, 6 бөлім, 5 тапсырма, 120бет	[1,12-1-9]		12 апта	есептер шығару
13.	Сызықгық теңдеулер жүйесін Монте-Карло әдісімең шешу Сызықтық жүйелерді айналдыру әдісімең шешу.	Монте-Карло әдісімен шешу ПОӘК, 6 бөлім, 6 тапсырма, 121бет	[1,12-1-9]		13 апта	есептер шығару
14.	Екінші ретті ЖДТ үшін шекаралық есепті шешудің жуык әдістері. Ату әдісі. Қума әдісі.	Ату әдісі. Қума әдісімен шешу ПОӘК, 6 бөлім, 6 тапсырма, 121бет	[1,12-1-9]		14 апта	есептер шығару
15.	Ұяшыктар әдісі. Анықталған интегапдарды біртіндеп есептеуге келтіру әдісі. Статистикалық сынау әдісі.	Статистикалық сынау әдісі. ПОӘК, 6 бөлім, 6 тапсырма, 121бет	[1,12-1-9]		15 апта	есептер шығару

СӨЖ-дің орындалу мерзімі және кестесі

№	Тақырып	Тапсырманың мақсаты мең мазмұны	Ұсынылатын әдебиеттер Негізгі/қосымша	Балл	Жұмыстардың көрсетілу мерзімі	Бақылау формасы
1.	Кіріспе.Математикалық модельдеу мең эксперимеңттеу ұғымы және қоршаған әлемді танудағы оның рөлі.	Математикалық модельдеу мең эксперименттеу ПОӘК, 6 бөлім, 1 тапсырма, 117бет	[1,12-1-9]		1 апта	реферат
2.	Қателер теориисының элементтері.Машиналық арифметика қателері туралы ұғым. Формула бойынша жуықтау есептеу тәсілдері.	Шектік абсолюттік қателіктерді қатаң ескере отырып есептеу ПОӘК, 6 бөлім, 1 тапсырма, 117бет	[1,12-1-9]		2 апта	есептер шығару
3.	Сызықтық емес теңдсулерді шешудің сандық әдістері. Хорда әдісі. Комбинациялау әдісі. Жай итерация әдісі. Теңдеуді итерациялық түрге түрлеңдіру. Итерациялық әдістердің геометриялық түсініктемесі. Функциялар мәндерін есептеуге Ньютон әдісін қолдану.	Хорда әдісі. Функциялар мәндерін есептеуге Ньютон әдісін қолдану ПОӘК, 6 бөлім, 2 тапсырма, 118бет	[1,12-1-9]		3 апта	Есептер шығару
4.	Сызықтық емес теңдеулер жүйесін шешудің сандық әдістері. Жай итерация әдісі. Ньютон әдісі және оның модификациялары. Сызықтық емес жүйелерді құлама әдісімең шешу.	Сызықтық емес жүйелерді кұлама әдісімең шешу ПОӘК, 6 бөлім, 2 тапсырма, 118бет	[1,12-1-9]		4 апта	Есептер шығару
5.	Сызықтық алгебра есептері. Матрицаның LU-жіктелуі. Сызыкгық жүйелерді LU-жіктелуі арқылы шешу. Сызықтық алгебралық теңдеулер жүйесін шешудің итерациялық әдістерінде дөңгелектеу әдістерінің рөлі туралы. Жетілдірілгең итерациялық әдістер.	Матрицаның LU-жіктелуі. ПОӘК, 6 бөлім, 3 тапсырма, 119бет	[1,12-1-9]		5 апта	Есептер шығару
6.	Функцияларды аппроксимациялау. Функциялар мәндерін Тейлор қатарымең,Чебышев көпмүшелерімең есептеу. Интерполяциялау. Сызыктық және квадратгық интерполяция. Kepi интерполяциялау.	Функциялар мәндерін Тейлор қатарымең, Чебышев көпмүшелерімең есептеу ПОӘК, 6 бөлім, 3 тапсырма, 119бет	[1,12-1-9]		6 апта	Есептер шығару
7.	Сандық диффереңциялдау. Интерполяциялык көпмүшелер негізінде сандық диффереңциалдау формулалары. Анықталмаған коэффициеңттер әдісі. Рунге формуласы	Анықталмаған коэффициеңттер әдісі. Рунге формуласы ПОӘК, 6 бөлім, 4 тапсырма, 120бет	[1,12-1-9]		7 апта	Есептер шығару
8.	Сандық интегралдау. Анықталған интегралдарды интегралдаудың сандық әдістері. Сплайндар әдісі. Еселі интегралдарды интегралдаудың сандық әдістері.	Еселі интегралдарды интегралдаудың сандық әдістері. ПОӘК, 6 бөлім, 4 тапсырма, 120бет	[1,12-1-9]		8 апта	Есептер шығару
9.	Жай диффереңциалдык теңдеулерді (ЖДТ) шешудің сандық әдістері. Бірінші ретті ЖДТ үшін Коши үшін есебін шешудің Адамс әдісі.	ЖДТ жүйесі үшін Коши есебін шешудің төрітінші ретті Рунге-Кутта әдісі ПОӘК, 6 бөлім, 4 тапсырма, 121 бет	[1,12-1-9]		9 апта	Есептер шығару
10.	Дербес туындылы диффереңциалдық теңдеулерді шешудің сандық әдістері.	Тасымалдаудың бірінші ретті сызықтық теңдеуді шешудің шектеулі- айырымдық әдістері ПОӘК, 6 бөлім, 4 тапсырма, 121бет	[1,12-1-9]		10 апта	Есептер шығару

Қолданылған әдебиеттер тізімі

Дата добавления: 2017-01-14