
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Тура жол алгоритмі 7 страница
|
|
|
|
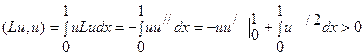 болатын u/º0 жалғыз мүмкін функция табылады және u≡0 болса, онда (Lu,u)=0 болады. Яғни L операторы оң оператор болады.
болатын u/º0 жалғыз мүмкін функция табылады және u≡0 болса, онда (Lu,u)=0 болады. Яғни L операторы оң оператор болады.
Вариациялық есеп
I=I[g(x)] (7.39)
функцияоналы К={g(x)} жиынында анықталған функционал болсын.
(7.39) функционалының экстремумдарын іздеу есебі вариациялық есеп деп аталады. Одан гөрі дәлірек айтсақ (1-сурет): g=g(х) барлық мүмкін функциялар үшін минимум жағдайында I[g]³I[g] теңсіздігі орындалатын немесе максимум жағдайында I[g]£I[ 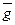 ] теңсіздігі орындалатын функцияға жеткілікті жуық
] теңсіздігі орындалатын функцияға жеткілікті жуық  функциясын табу керек. g және
функциясын табу керек. g және 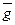 функцияларының ара қашықтығын әртүрлі түсінуге болады.
функцияларының ара қашықтығын әртүрлі түсінуге болады.
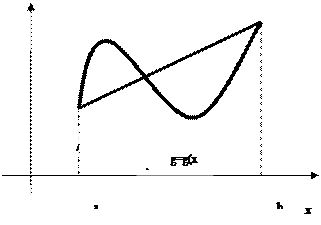
1-сурет. (7.39)-есептің геометриялық мағынасы.
1-мысал: М(а,А) және N(b,B) нүктелерінен өтетін g=g(х) жатық қисықтары арасынан доғасының ұзындығы ең кіші түзуді табу керек болсын.
Есеп С(1)[a,b] класына жататын g=g(х) қисықтары үшін және g(а)=А, g(b)=B болатын келесі функционалдың минимумын табуға келеді:

Геометриялық мағынасына көңіл аударсақ: ізделінді түзу
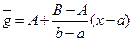
 болады.
болады.
Негізгі теоремалар.
Г шекаралы G облысында үзіліссіз коэффициентті (қарапайым немесе дербес туындылы) сызықты дифференциалдық теңдеу берілсін және осы теңдеудің Г шекарасында берілген шекаралық біртекті шарттарды қанағаттандыратын g шешімін табу керек болсын. Бұл теңдеудің сол жағын G+Г облысында жеткілікті үзіліссіз туындылары бар және Г шекарасында шекаралық шарттарды қанағаттандыратын К функциялар жиынында анықталған L сызықты оператор ретінде қарастыруға болады. Сонда есеп келесі операторлық теңдеуді шешуге келеді:
Lg=f(P), (7.40)
R[g]=0, (7.41)
Мұндағы Р тәуелсіз айнымалылар тобы, f(P) функциясы - gÎK болатын үзіліссіз берілген функция, сонымен қатар g функциясы Г шекарасында шекаралық шартты қанағаттандырсын. R – белгісіз сызықты, төмен ретті оператор.
Lg=f(P) (7.42)
R[g]=j(P), РÎГ, (7.43)
(мұндағы j(P) – белгілі функция) біртекті емес шектік есеп
R[g1]= j(P) (7.44)
біртекті шектік есепке келтіріледі, егер g=z+g1 болып, мұндағы z-жаңа белгісіз және g1 – (7.43)-шартты қанағаттандыратын жеткілікті жатық функция болса. (7.42) және (7.43) формулалардан Lz=f(P) –Lg1 және R[z]=0 екенін аламыз. g1 функциясын таңдау арқылы табуға болады. Сонда бұл әдістің идеясы - (7.39)-(7.40) – шектік есепті әлдебір функционалға минимум немесе экстремум беретін теңсалмақты есеппен алмастыруға келтіру. Практикада өзімізге таныс белгілеулермен жұмыс жасау үшін g функциясын y деп белгілеуге болады.
Т е о р е м а 1. L операторы – К класында анықталған және оң симметриялы сызықты оператор болсын. Онда (7.39)-операторлық теңдеу (7.40)-шекаралық шартпен бірге К класында екі шешім қабылдай алмайды, яғни егер шектік есептің шешімі бар болса, ол міндетті түрде жалғыз болады.
Екінші ретті қарапайым дифференциалдық теңдеу үшін құрылған сызықты шектік есепті вариациялық есепке келтіру.
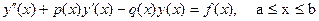 (7.47)
(7.47)
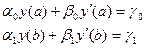 (7.48)
(7.48)
есебі берілсін. Бұл есептің шешімін келесі түрде іздейміз:

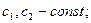 (7.49)
(7.49)
Мұндағы z(x) функциясы - шекаралық шарттары біртекті болатын біртекті емес теңдеудің шешімі:
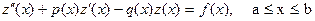 (7.50)
(7.50)
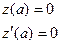
Ал z1(x) функциясы – шекаралық шарттары біртекті емес болатын біртекті теңдеудің шешімі:
 (7.51)
(7.51)

Ал z2(x) функциясы – шекаралық шарттары біртекті емес болатын біртекті теңдеудің шешімі болады:
 (7.52)
(7.52)

(7.50)-(7.52)- есептерді шешіп, (7.49)-формула мен (7.48)-шекаралық шарттарды қолданып с1 және с2 коэффициенттерін анықтайтын жүйені құруға болады.
 (7.53)
(7.53)
(7.53)-жүйені шығару арқылы у(х) белгісізін тауып, оны (7.47)-(7.48)-есепке қою арқылы шектік есепті шешеміз.
Мысалы:
 (7.54)
(7.54)
Шешуі:
1. Біртекті шекаралық шартты біртексіз теңдеу құрамыз:
 (7.55)
(7.55)
2.Біртексіз шекаралық шартты біртекті теңдеу құрамыз:
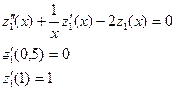 (7.56)
(7.56)
3.Біртексіз шекаралық шартты біртекті теңдеу құрамыз:
 (7.57)
(7.57)
4. (7.55)-(7.57)-есептерді 1-ретті дифференциалдық теңдеулер жүйесі үшін Коши есебіне келтіреміз:
T(x)=z(x), 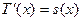 белгілеулерін енгізейік. Сонда
белгілеулерін енгізейік. Сонда
 (7.58)
(7.58)
T1(x)=z1(x),  белгілеулерін енгізейік. Сонда
белгілеулерін енгізейік. Сонда
 (7.59)
(7.59)
T2(x)=z2(x), 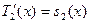 белгілеулерін енгізейік. Сонда
белгілеулерін енгізейік. Сонда
 (7.60)
(7.60)
есептері құрылады. Бұл есептердегі Т(х), T1(x), T2(x) функциялары (7.55-(7.57)-есептердің шешіимдері болады, ал  функциялары осы шешімдердің туындылары болады.
функциялары осы шешімдердің туындылары болады.
5. Т(х), T1(x), T2(x) функциялары табылған соң (7.53)-формула бойынша с коэффициенттерін табуға арналған жүйе құрамыз:

екенін ескерсек, 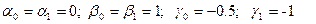 болады.
болады.
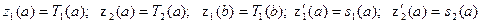 екенін ескеріп, (7.53)-ке қойсақ:
екенін ескеріп, (7.53)-ке қойсақ:  сонда
сонда 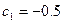 болады. Келесі теңдеуіне қойсақ:
болады. Келесі теңдеуіне қойсақ:
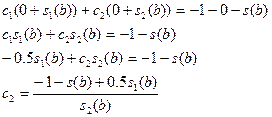
6. с2-ні табу үшін алдымен (7.58)-(7.60)-есептерді Эйлер әдісімен шешіп Т(хk), T1(xk), T2(xk),  мәндер кесте сын құру керек. Сосын с2-ні тауып
мәндер кесте сын құру керек. Сосын с2-ні тауып 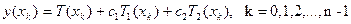 формуласына қою арқылы у(хk) шешімдерін тауып алуға болады.
формуласына қою арқылы у(хk) шешімдерін тауып алуға болады.
Галеркин әдісі.
Вариациялық, ақырлы-айырымдық әдістерді қолдану барысында шектік есептің шешімі кесте лық мәндер түрінде алынады. Ал Галеркин әдісі аналитикалық әдіске жатады.
y // +p(x) y / + q(x) y = f(x) (7.61)
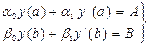 (7.62)
(7.62)
мұндағы p(x), q(x), f(x) – функциялары [a,b] аралығында үзіліссіз функциялар, ал a0,a1,b0,b1, A,B –берілген тұрақтылар және ½a0½+½a1½¹0, ½b0½½b1½¹0 шектік есебі берілсін.
Белгілеу енгізейік:
L[y]=y // +p(x) y / + q(x) y (7.63)
 (7.64)
(7.64)
[a,b] аралығында базистік функциялар жүйесі берілсін
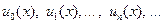 (7.65)
(7.65)
және олар келесі шарттарды қанағаттандырсын:
1 (7.65)-жүйе ортогональды болсын, яғни
 (7.66)
(7.66)
2 (7.65)-жүйе толық жүйе болсын, яғни 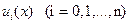 барлық функцияларына ортогональ нөлден өзгеше басқа бір де бір функция жоқ болсын.
барлық функцияларына ортогональ нөлден өзгеше басқа бір де бір функция жоқ болсын.
3 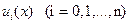 ақырлы базистік функциялар жүйесі төмендегі біртексіз (7.67)-шарттарды қанағаттандыратындай болып, ал
ақырлы базистік функциялар жүйесі төмендегі біртексіз (7.67)-шарттарды қанағаттандыратындай болып, ал  функциялары төмендегі біртекті (7.68)-шарттарды қанағаттандыратындай болып таңдалынып алынуы керек:
функциялары төмендегі біртекті (7.68)-шарттарды қанағаттандыратындай болып таңдалынып алынуы керек:
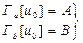 (7.67)
(7.67)
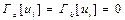 (7.68)
(7.68)
(7.61)-(7.62)-шектік есептің шешімін
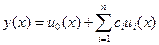 (7.69)
(7.69)
түрінде іздейміз. (7.67), (7.68)-шарттардан бұл функцияның (7.62)-шартты қанағаттандыратыны көрінеді.
Байныспаушылық (невязка) өрнегін қарастырамыз:
 (7.70)
(7.70)
сi коэффициенттерін байналыспаушылықтың квадратының интегралының мәні
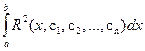 (7.71)
(7.71)
өте аз шама болатындай етіп таңдап алу керек. Бұл тек қана байланыспаушылық базистік функциялардың барлығына ортогональды болса ғана орындалатыны дәлелденген ([2], [13], [18] қараңыз).
Ортогональдылық шарты:
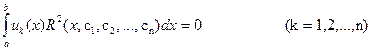
немесе
 (7.72)
(7.72)
(7.72)-ден сызықты алгебралық теңдеулер жүйесін аламыз, оны сi-ға қатысты шешу керек болады. Мұндай жүйені шешудің сандық әдістерін жоғарыда келтіргенбіз.
Мысалы:
Галеркин әдісін қолданып
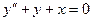 (7.73)
(7.73)
у(0)=у(1)=0 (7.74)
шектік есептің шешімін табу.
Ui базистік функциялар жүйесін таңдап аламыз:

Бұл функциялар сызықты тәуелсіз және нөлдік шекаралық шарттарды қанағаттандырады. Жуық шешімін мына түрде іздейміз:
 (7.75)
(7.75)
Бұл теңдеуді (7.73)-теңдеудің сол жағына қою арқылы байланыспаушылықты аламыз:
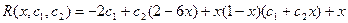 . (7.76)
. (7.76)
R функциясының u1(x) және u2(x) функцияларына ортогональдылығын ескерсек:
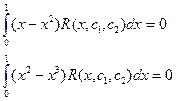
Бұл жүйеге (7.77) – шешімді қойсақ және интегралды есептесек, келесі сызықты алгебралық теңдеулер жүйесін аламыз:
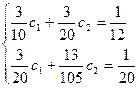
Бұл жүйені шешсек  . Бұл мәндерді (7.76)-ға қойсақ:
. Бұл мәндерді (7.76)-ға қойсақ:
 .
.
Бұл есептің дәл шешімі  . Берілген аралықты 0,25 қадаммен бірнеше бөлікке бөліп әр нүктедегі функция мәндерін алып салыстырсақ, төмендегі 22-кестеден қателігінің қаншалықты екенін анықтауға болады.
. Берілген аралықты 0,25 қадаммен бірнеше бөлікке бөліп әр нүктедегі функция мәндерін алып салыстырсақ, төмендегі 22-кестеден қателігінің қаншалықты екенін анықтауға болады.
22-кесте. (7.73-7.74)-есептің мәндер кестесi.
| xi | 0.25 | 0.50 | 0.75 |
| yi | 0.044 | 0.069 | 0.060 |
| Y | 0.044 | 0.070 | 0.050 |
Егер (7.61)-теңдеудің коэффициенттерін есептеу қиынға соғатын болса бұл әдістен гөрі ақырлы-айырымдық немесе қуалау әдістерінің бірін қолдануға болады.
11-ДӘРІС. Дербес туындылы математикалық физиканың теңдеулеріне сандық әдістер.
1. Бір өлшемді параболалық теңдеулер.
2. Жылу өткізгіштік теңдеуі үшін аралас Коши есебіне сәйкес келетін айқындалмаған айырымдық есептер.
3. Тор және торда аппроксимациялау.
4. Айырымдық есептің орнықтылығын зерттеу әдістері, айнымалыны бөлектеу, спектр, энергетика теңсіздігі және максимум принциптерін пайдалану.
Дәріс тезисі:
Жалпы түрде сызықты емес дербес туындылы дифференциалдық теңдеу
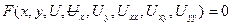 (1)
(1)
түрінде жазылады.
(1)-теңдеуді теңбе – теңдікке айналдыратын  функциясын оның шешімі деп атайды.
функциясын оның шешімі деп атайды.
Сызықты дербес туындылы дифференциалдық теңдеу
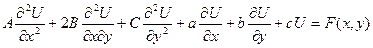 (2)
(2)
түрінде жазылады. Бұл теңдеудің коэффициенттері де х,у айнымалыларынан тәуелді. Егер олар х,у-тен тәуелсіз болса, онда теңдеу тұрақты коэффициентті деп аталады.
(2)-теңдеудің дискриминанты:  формуласымен табылады.
формуласымен табылады.
D>0 болса, (2)-теңдеу эллиптикалық типті теңдеу,
D=0 болса, (2)-теңдеу параболалық типті теңдеу,
D<0 болса, (2)-теңдеу гиперболалық типті теңдеу, егер D таңбасы тұрақты таңба сақтамаса онда аралас типті теңдеу деп аталады.
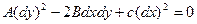 (3)
(3)
(3)-теңдеу (2)-теңдеудің характеристикалық теңдеуі деп аталады.
Жалпы жағдайда (1)-(2)-теңдеулердің шешімі шексіз көп болады. Сондықтан мұндай теңдеулерді шешу үшін оларға қосымша бастапқы және шекаралық шарттар беріледі.
Егер бір айнымалы уақыттан тәуелді болса, оған қатысты шарт бастапқы шарт деп аталады. Келесі айнымалы кеңістіктегі кординаттар болып, тұрақтандырылған белгілі бір нүктелердегі мәндерді көрсетсе, оған қатысты шарт шекаралық шарт деп аталады.
Егер теңдеу тек қана кеңістіктік координаттардан тәуелді болса, яғни уақытқа байланыссыз өзгеретін процесстерді сипаттаса, онда стационар дифференциалдық теңдеу деп аталады. Оған Гельмгольц теңдеуі, Пуассон теңдеуі үшін Дирихле есебі жатады. Ал теңдеу уақыт айнымалысынан тәуелді болып, қандай да бір процестің уақыт өзгеруіне байланысты мәндерін анықтауға қатысты болса, онда стационар емес теңдеу деп аталады. Оған Толқын теңдеуі, жылуөткізгіштік теңдеуі жатады.
Мұндай теңдеулерді шешу үшін практикада тор әдісі көп қолданылады. Тор әдісі 3 этаптан тұрады:
1. Тор құру
2. Айырымдық схема құру
3. Айырымдық схеманың орнықтылығы мен жинақтылығын зерттеу
Стационар емес дербес туындылы дифференциалдық теңдеулерді шешудің тор әдісі.
Дифференциалдық операторды дискретті нүктелердегі функция мәндері арқылы өрнектелген өздерінің жуық мәндерімен алмастыру арқылы шешуді тор әдісі дейді.
Жылуөткізгіштік теңдеуін қарастырайық. Біртекті жұқа, бірлік өлшемді серіппеде жылудың таралуын уақытқа байланысты анықтау керек болсын.
 (1)
(1)
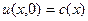 (2)
(2)
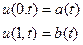 (3)
(3)
Мұндағы  - тұрақты, жылуөткізгіштік коэффициенті,
- тұрақты, жылуөткізгіштік коэффициенті, 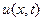 - температура,
- температура, 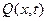 - жылу көзінің таралу функциясы, t – уақыт. (2)-шарт – бастапқы уақыт моментінде серіппедегі температураның таралуы. (3)-шарт – уақытқа байланысты серіппенің екі ұшындағы температураның өзгеру заңдылығы. Кез келген уақыт моментінде (t>0) серіппедегі температураның
- жылу көзінің таралу функциясы, t – уақыт. (2)-шарт – бастапқы уақыт моментінде серіппедегі температураның таралуы. (3)-шарт – уақытқа байланысты серіппенің екі ұшындағы температураның өзгеру заңдылығы. Кез келген уақыт моментінде (t>0) серіппедегі температураның 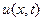 таралуын табу керек.
таралуын табу керек.
1. Тор құрамыз: Серіппені қандай да бір шекарасы Г болатын D тұйық облысында қарастырайық. D облысының ішінде жататын тордың төрт көршісі бар түйіндері ішкі түйіндер деп аталады. Барлық ішкі түйіндер жиыны торлық облыс деп аталады. Егер түйіннің қандай да бір көршісі D облысынан тыс жатса оны шекаралық түйін дейді.  тұрақтандырылған уақыт моментіне сәйкес
тұрақтандырылған уақыт моментіне сәйкес 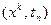 түйіндер жиыны n-ші уақыт қабаты деп аталады. Тор түйіндерінің координаттары
түйіндер жиыны n-ші уақыт қабаты деп аталады. Тор түйіндерінің координаттары 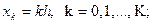
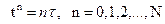 немесе
немесе 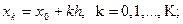
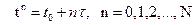 деп анықталсын. Мұндағы h – тордың кеңістік бойынша қадамы,
деп анықталсын. Мұндағы h – тордың кеңістік бойынша қадамы,  - тордың уақыт бойынша қадамы болсын.
- тордың уақыт бойынша қадамы болсын.
2. Айырымдық схема құрамыз: Үзіліссіз 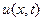 және
және 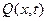 функцияларының орнына торлық функция қарастырамыз. Құрылған тордың түйіндерінде анықталған функцияны торлық функция дейміз.
функцияларының орнына торлық функция қарастырамыз. Құрылған тордың түйіндерінде анықталған функцияны торлық функция дейміз.
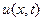 орнына торлық
орнына торлық  немесе
немесе  функцияларын,
функцияларын, 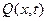 функциясының орнына торлық
функциясының орнына торлық 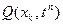 немесе
немесе  функцияларын қарастырамыз. Сонда (1)-(3)-есептің шешімі
функцияларын қарастырамыз. Сонда (1)-(3)-есептің шешімі  торлық нүктелерде
торлық нүктелерде  - сандық мәндер таблицасын анықтауға келтіріледі. Ол үшін дифференциалдық теңдеуді айырымдық теңдеумен алмастырамыз: туықдыларды жуықтаушы айырымдық қатынастармен ауыстыру арқала. Бастапқы және шекаралық шарттарды да сәйкес айырымдық қатынастармен ауыстырамыз.
- сандық мәндер таблицасын анықтауға келтіріледі. Ол үшін дифференциалдық теңдеуді айырымдық теңдеумен алмастырамыз: туықдыларды жуықтаушы айырымдық қатынастармен ауыстыру арқала. Бастапқы және шекаралық шарттарды да сәйкес айырымдық қатынастармен ауыстырамыз.
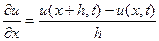 қатынасын қолданып
қатынасын қолданып
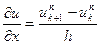 (4)
(4)
деуге болады. Дәл сол сияқты:
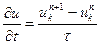 (5)
(5)
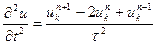 (6)
(6)
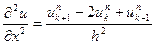 (7)
(7)
(4)-(7) қатынастарын (1)-ге қойсақ, айырымдық теңдеу аламыз
 . (8)
. (8)
Бастапқы шекаралық шарттар келесі түрде жазылады:
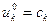 (9)
(9)
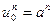 (10)
(10)
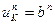
Сонымен берілген (1)-(3)- дифференциалдық есепті (8)-(10) торлық-айырымдық немесе шектік-айырымдық есепке келтірдік. (8)-(10)- есепті практикада шектік-айырымдық схема деп атайды.
Бұл есепті шешу үшін (8)-теңдеуден белгілі уақыт қабатынан келесі уақыт қабатына өткен уақыттағы температураның таралуын анықтайтын формуланы шығарамыз:
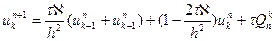 (11)
(11)
(9)-(10)-шарттарды ескерсек (11)-схемадан кез келген уақыт моментінде температураның стержень бойымен таралуын анықтауға болады.
12-ДӘРІС. Гиперболалық теңдеулер.
1. Бір өлшемді тасымалданудың теңдеуіне аралас Коши есебі.
2. Есептің дұрыс қойылуы үшін характеристиканың маңызы.
3. Айқындалдалмаған айырымдық схемалар.
4. Олардың аппроксимациясы мен орнықтылығын зерттеу.
5. Компьютерде сандық шешімін табу алгоритмі.
6. Бір өлшемді толқын теңдеуі үшін аралас Коши есебіне сәйкес келетін айырымдық схемалар.
7. Аппроксимациясы және орнықтылығы.
8. Сандық шешімін табу алгоритмі.
Дәріс тезисі:
1.1. Шекаралық есептер
Сызықтық эллипстік теңдеулер теориясында шекаралық есептер елеулі орын алады. Олар дифференциялдық теңдеудің белгілі бір облыстың ішінде анықталған және оның шекарасында тиісті шарттарды қанағаттандыратын шешімін анықтауды талап етеді.
Шекаралық есептерді шешу Коши есептеріне қарағанда әлдеқайда күрделі мәселе. Себебі соңғы есептедің шешімдері сандық әдістер арқылы рекурентті формулалармен анықталатын болса, ал шекаралық есептерге қолданылатын сандық әдістер алгебралық теңдеулер жүйесін шешуге алып келеді. Сонымен қатар есеп өлшемінің, яғни айнымалылар санының өсуі қосымша қиындықтар туғызады.
Мұнда біз негізінен 2-ретті дифференциалдық теңдеулерге қойылатын шекаралық есептерді қарастырамыз. Оларды сызықтық алгебралық теңдеулер жүйесіне келтіру және оны шешу жолдарын зерттейміз.
Алдымен эллипстік теңдеулерге қандай шекаралық есептер қоюға болатынын анықтап алайық. Жоғарыда айтылғандай біздің негізгі қарастыратынымыз
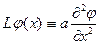 +b
+b 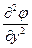 +c
+c  +d
+d 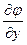 +e
+e 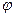 =f (5)
=f (5)
түріндегі дифференциалдық теңдеулерге қойылатын есептер.Мұндағы a,b,c,d,e және f жалпы жағдайда x және y тәуелсіз айнымалыларының функциялары. Сондай-ақ олар шекарасы Г болған G(x,y) облысында анықталған және үзіліссіз функциялар деп есептеледі. (5) теңдеуі эллипстік түрдегі теңдеу болуы үшін G=G 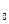 +Г-да a>0 және b>0 шарттарының орындалуын талап етеміз.Сондай-ақ G-да l
+Г-да a>0 және b>0 шарттарының орындалуын талап етеміз.Сондай-ақ G-да l  0 деп қабылдаймыз.
0 деп қабылдаймыз.
|
|
|
|
|
Дата добавления: 2017-01-14; Просмотров: 1130; Нарушение авторских прав?; Мы поможем в написании вашей работы!