Тура жол алгоритмі 10 страница

Осы айырымдық схеманың шешімін анықтау жолдарын қарастырайық.

Алдымен (57)-(58) есебін мынадай түрде жазайық

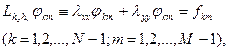(59)

(60)

Мұндағы және операторлары

және

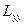мағынадағы және осьтері бойынша алынған айырымдық операторлар. Олар біріншіден, әрбір бекітілген нүктесінде және дербес туындыларына жуықталады. Сондықтан және операторларының негізгі қасиеттері және айырымдық операторлары үшін де сақталады. Мәселен, және 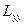–теріс анықталған және өзіне түйіндес операторлар. Ендеше және –те теріс анықталған және өзіне түйіндес операторлар. Екіншіден, егер және айырымдық операторларын (57)-(58) есебіне байланыстырмай, өз алдына дербес түрде қарастыратын болсақ, онда шекті өлшемді Евклид кеңістігінде оларға

және

сияқты симметриялы квадрат матрицалар сәйкес келеді. Соңғы матрицалар теріс анықталған матрицалар және олардың меншікті сандары

түрінде анықталады. Сол себепті де

(59)-(60) –сызықтық алгебралық жүйе. Әдетте мұндай жүйелерді шешу үшін дәл немесе итерациялық әдістер қолданылады (59)-(60) айырымдық есебін алгебралық жүйеге келтірмей-ақ, оған тікелей қолдануға болатын және алгоритмдері есептеуге жеңіл үш түрлі итерациялық әдіске қысқаша тоқталамыз.

Алдымен (59) теңдеуінің екі жағын да (-1)-ге көбейтеміз,

Сонда

- (61)

яғни

Мұндағы және –оң анықталған операторлар және

Сондай-ақ

Мұндағы –оң анықталған симметриялы оператор және .

Итерациялық әдістердің жинақтылығын зерттеуді жеңілдету мақсатымен және деп есептейміз.

1.4.1. Жай итерациялық әдіс

Бұл әдісті қолдану үшін (57)-(58) айырымдық есебін басқаша түрде жазамыз

(62)

(63)

Содан кейін қандай да бір (мәселен, 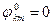) бастапқы жуықтауын таңдап алып, келесі итерациялық әдісті құрамыз

(64)

Бұл әдіс сандық әдістер теориясында жай итерациялық деп аталады. Оның есептеу алгоритмі оңай жүзеге асырылады, тек әрбір итерациялық қадамында шекаралық шарты ескертілуі тиіс.

Енді (64)әдісінің жинақтылығын зерттейміз. Олүшін (64) өрнегін мынадай түрге келтіреміз:

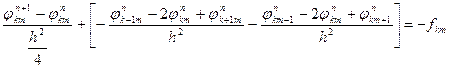
(65)

яғни

Соңғы әдіс –белгілі жай итерациялық әдіс болып табылады. Жалпы теория бойынша ол жинақты болуы үшін оң анықталған оператор және болуы тиіс. Қарастырылып отырған жағдайда аталған талаптар орындалады, өйткені жоғарыда айтылғандай және –оң анықталған операторлар, демек, -та оң анықталған оператор. Сондай-ақ

Олай болса ,яғни .

Сонымен қатар (65) –тиімді итерациялық әдіс, себебі параметрінің тиімді мәні

Ендеше (65) –жинақты итерациялық әдіс. Ал ол жинақталатын болас, онда оның шегі (57)-(58) айырымдық есебінің шешімін беретіні анық.

Айталық, (55)-(56) Дирихле есебінің жуық шешімін дәлдікпен анықтау керек болсын. Онда дәлдігі сол –ге тең жуық шешімді табу үшін (64) әдісінде

итерация жасау керек екендігі белгілі. Мұндағы ал . Қарастырылып отырған жағдайда , . Ендеше яғни берілген дәлдікпен жуық шешімді табу үшін шамасындай итерация жасалуы тиіс.

ЗЕРТХАНАЛЫҚ ЖҰМЫСТАРДЫ ЖҮРГІЗУГЕ

АРНАЛҒАН ӘДІСТЕМЕЛІК НҰСҚАУЛАР

Тақырыбы: Қателіктерді есептеу және талдау

Мақсаты: Қателіктер теориясымен таныстыру және оларды есептеу жолдарын үйрету

Тапсырма:

1 мысал: 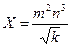, мұндағы , , ; Есептеу және нәтижелердің қателіктерін анықтау керек.

2 мысал: , мұндағы , ; Есептеу және нәтижелердің қателіктерін анықтау керек.

3 мысал: , мұндағы , . Есептеу және нәтижелердің қателіктерін анықтау керек.

4-мысал: ; берілген. Санның дұрыс цифрларын анықтау.

5-мысал: көбейтіндісінің абсолютті және салыстырмалы қателіктерін анықтау.

6-мысал: Х=2,1514 санын 3 мәнді цифрға дейін дөңгелектеп, абсолютті және салыстырмалы қателіктерін табу.

Тапсырманы орындауға әдістемелік нұсқаулар:

1 мысал: 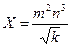, мұндағы , , ; Есептеу және нәтижелердің қателіктерін анықтау керек.

Шешуі:

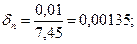
Ары қарай, 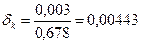, бұдан

.

Жауабы: .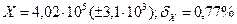

2 мысал: , мұндағы , ; Есептеу және нәтижелердің қателіктерін анықтау керек.

Шешуі: ;

; ; ;

. Жауабы: ; .

3 мысал: , мұндағы , . Есептеу және нәтижелердің қателіктерін анықтау керек.

Шешуі:

Жауабы: .

4- мысал: Берілген х санының дұрыс цифрлар санын анықтау керек болсын.

; .

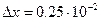Анықтама бойынша: шарты орындалса, 3 цифрын дұрыс цифр деуге болады. Шындығында 0,0025<0,05 екен, яғни 3 - дұрыс цифр. 9 цифрын тексерсек: 0,0025<0,005, яғни 9 цифры да дұрыс. Ал 4 пен 1 цифрлары үшін 0,0025<0,0005 және 0,0025<0,00005 болғандықтан, олар күмәнді цифрлар болады. Қорыта айтқанда үтірден кейінгі 3 және 9 цифрларын жоғалтпау керек, яғни санды 0,39 деп дөңгелектеуге болады, 0,4 деп дөңгелектесек дөңгелектеу қателігі өсіп кетеді. Санның дұрыс цифрлар саны төртеу.

5-мысал: ; берілген. Санның дұрыс цифрларын анықтау.

Анықтама бойынша: , яғни . Одан шығатыны: . Енді санның цифрларын тексереміз:

8 цифры - дұрыс, өйткені: .

9 цифры – күмәнді, өйткені: . Дәл осылай 2 және 1 цифрларының да күмәнді екенін анықтауға болады. Сонда а санының 2 цифры дұрыс.

6-мысал: Х=2,1514 санын 3 мәнді цифрға дейін дөңгелектеп, абсолютті және салыстырмалы қателіктерін табу.

болады. Сонда , .

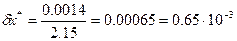Бақылау сұрақтары:

1. Абсолютті қателік дегеніміз не?

2. Салыстырмалы қателік?

3. Көбейтіндінің қателігі қалай есептеледі?

Қосындының қателігі?

Тақырыбы: Бейсызықты бір теңдеудің сандық шешімін табу (аралықты екіге бөлу, итерация, Ньютон әдісі)

Мақсаты: Сызықтық емес теңдеулерді шешудің сандық әдістерімен танысу.

Тапсырма:

1-мысал: Берілген теңдеудің түбірін анықтау:

теңдеуінің түбірін қарапайым итерация, хорда және Ньютон әдісімен табу керек болсын.

Тапсырманы орындауға әдістемелік нұсқаулар:

1-мысал: Берілген теңдеудің түбірін анықтау:

(2.1)

Теңдеудің түбірі жатқан аралықты аналитикалық тәсілмен табамыз: ол үшін функция туындысын тауып, оны нөлге теңестіру арқылы экстремумдарын анықтаймыз: , экстремумы: х₁=Ln10=2,3;

Экстремум нүктелеріндегі функция таңбасының кестесін толтырамыз.

Кесте 1. функциясының таңбасын анықтау.

Нүктелер		2,3
sign(f)	+	-	+

Функция таңбасының ауысуы (; 2,3] және [2,3; ) аралығында байқалды. Яғни осы аралықта теңдеудің түбірі бар.

Енді графиктік әдісті қарастырайық. Ол үшін теңдеуді мына түрлерге жіктейміз, себебі функция күрделі, трансцендентті, бірден графигін құруға болмайды: . Екі функцияның графигін саламыз, екеуінің қиылысқан нүктесі теңдеудің түбірі болып табылады (1-сурет). Қиылысу нүктелерінің аймақтарын анықтаймыз.

1-сурет. функцияларының графиктері.

Бірінші түбірі [0,1] аралығында, ал екінші түбірі [2,6] аралығында жататыны суретте көрініп тұр. Енді осы аралықтағы қай нүкте (2.1)-ші теңдеуді қанағаттандыратынын анықтаймыз.

Кесіндіні қақ бөлу әдісі

(2.1) - теңдеуді кесіндіні қақ бөлу әдісімен шешу алгаритмі келесі қадамнан тұрады.

9. (2.1)-ші теңдеудің түбірі жатқан аралығын анықтау және осы аралықта түбірдің жалғыздығын тексеру. Яғни x осі бойында бірдей қашықтықта жатқан нүктелердегі функцияның мәндерін есептеміз, және егер екі шеткі нүктеде немесе екі көрші нүктеде функция мәндерінің таңбалары әр түрлі болса, онда сол аралықта түбір бар деп есептеу

10. Осы аралықты қаққа бөлу және ол нүктенің мәнін

X_орт=(X_n+1+X_n)\2. (2.2)

формуласымен анықтау.

11. X_n+1-X_n<e шарты арқылы қарастырылып отырған аралықтан шығып кетпеуді бақылаймыз.

12. X_ОРТ нүктесіндегі функция мәнін F(X_ОРТ) есептеу.

13. Егер оның таңбасы F(X_n) функциясының таңбасымен бірдей болса, X_n нүктесінің орнына X_ОРТ нүктесін қарастырамыз.

14. Ал егер F(X_ОРТ) функциясының таңбасы F(X_n+1) функциясының таңбасымен бірдей болса, X_n+1 нүктесінің орнына Х_ОРТ нүктесін қарастырамыз.

15. Шыққан аралықтар [X_n,, Х_орт] U [X_орт, X_n+1] белгіленеді.және алдыңғы шарттарға байланысты екі аралықтың біреуін тағы қаққа бөлу арқылы ізделінді нүктеге біртіндеп жақындаймыз. Яғни мына шарттар тексеріледі: F(X_n+1)*F(X_орт)<0 шарты орындалса [X_орт,X_n+1] аралығы қаққа бөлінеді де шыққан нүкте мәні, X_ОРТ2=X_ОРТ+ X _n+1/2 формуласымен есептеледі. F(X_n)*F(Х_ОРТ)<0 шарты орындалса [X_n, X_орт] аралығы қаққа бөлініп, табылған нүкте X_ОРТ2=X_ОРТ+ X _n/2 формуласымен есептеледі.

16. Осы процесті іздеп отырған х нүктесіне жеткенге дейін жалғастырып, X_ОРТ, X_ОРТ2, X_ОРТ3, …, X_ОРТN тізбегін құрамыз. Мына шарт орындалатын уақытта X_ОРТN - X_ОРТN-1 <E іздеу процесін тоқтатамыз да X_ОРТN нүктесін (2.1)-ші теңдеуді қанағаттандыратын х дәл түбірге жуық мән деп қабылдаймыз.

теңдеуінің түбірін қарапайым итерация әдісімен табу керек болсын. Теңдеуді итерациялық түрге келтіреміз:

. Ал және барлық х нүктелері үшін

. Яғни q=0,1 деп алып, бастапқы жуықтауды х₀=0 десек шарты орындалғанша итерациялық процесті құрамыз: х₀=0: 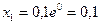; 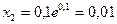, т.с.с. Түбір мәні х₆=0,111833, итерация саны 5-ке тең.

Хорда әдісі

Бұл әдіс кесіндіні қаққа бөлу әдісіне қарағанда шешімге тез жинақталады.

Алгоритмі:

5. х_n, x_n+1 аралығында f (x) және f (x_n+1) функцияларының таңбасы бір біріне қарама-қарсы және түбірі бар болсын.

6. Осы екі шеткі нүктеден хорда жүргізіп, хорданың х осімен қиылысқан нүктесін мына формуламен анықтаймыз.

(2.4)

7. х^* нүктесіндегі функция мәнін F(x^*)-ны есептеу. Оның таңбасын екі шеткі нүктедегі функцияның таңбасымен салыстырылады. Егер f (x_n) және f(x^*) функциясының таңбасы бірдей болса, онда хорданы x_n+1 және x^* нүктесі арқылы жүргізіледі. Оның мәнін (2.4) формуламен табады. Егер f(x_n+1) мен f(x^*) функцияның таңбалары бірдей болса, онда хорданы x_n және x^* нүктесі арқылы жүргізіледі. Шыққан нүктенің мәні (2.4) формуламен есептелінеді.

8. x^* нүктедегі мәнін есептеп, мәні нөлге жуық болса , онда x^* нүктесі (2.1) теңдеудің түбірі деп аталады. Егер нөлге жуық болмаса, онда процесс жалғасады.

Алдындағы мысал үшін программасы келесідей болады:

Ньютон әдісі

Алдыңғы әдістерге қарағанда бастапқы жуықтау дұрыс таңдалынып алынса Ньютон әдісі тез жинақталады. Бұл әдіске қатысты теореманы келтіре кетейік:

Дата добавления: 2017-01-14