Тура жол алгоритмі 11 страница

Теорема 1.3.: f(x) функциясы [a,b] аралығында анықталған және екі ретті туындысы бар, осы аралықта түбір жатыр f(a)*f(b)<0, туындылардың таңбалары осы аралықта тұрақты болса f(x)*f^'(x)>0, онда f(x₀)*f^''(x₀)>0 теңсіздігін қанағаттандыратын бастапқы жуықтаудан бастап (2.1)-ші теңдеуді қанағаттандыратын [a,b]-да жататын жалғыз шешімге жинақталатын итерациялық тізбек құруға болады.

Ньютон әдісінің геометриялық мағынасы: координаталары (x_n;f(x_n)), болатын нүктеден қисыққа жанама жүргізсек, оның ох өсімен қиылысу нүктесі теңдеудің түбіріне х_n+1 – кезекті жуықтау болып табылады.

Түбірге n-ші жуықтаудың қателігін бағалау үшін келесі теңсіздіктің орындалуын қадағалау керек: . Мұндағы М₂ – функцияның екінші ретті туындысының аралықтағы максимумы, m₁- минимумы. Егер, болса, онда болады, яғни түбірге дұрыс жуықталынса, әр итерациядан кейін кезекті жуықтаудың ондық таңба саны екіге артады да процесс тез жинақталады. Егер түбірді берілген е дәлдікпен табу керек болса, итерациялық процесті 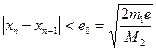шарты орындалғанша жалғастырамыз.

Бұл біртіндеп жуықтау әдісі деп аталады. Әдістің жинақталу жылдамдығы х₀ бастапқы нүктені дұрыс таңдауға байланысты. Егер итерация процесінде функцияның туындысы нөлге тең болса, қисыққа жүргізілген жанама осіне параллель болса, онда бұл әдісті қолдану қиындайды. Сол сияқты функцияның екінші ретті туындысының мәні шексіз үлкен болса және функцияның өзі бірінші ретті туындысы нөлге тең болса, онда шыққан түбірлер еселі болып, жинақталмауы мүмкін. Бұл әдісті қолдану үшін функциясы үзіліссіз және дифференциалданған болуы керек.

бастапқы жуықтауды таңдалынған уақытта құрылатын тізбек монотонды кемімелі болуы керек.

Алгоритмі:

1. Қисықтың бойынан қандайда бір нүктесін таңдап, осы нүкте арқылы қисыққа жанама жүргізіледі.

2. Жанама осін қиған кезде табылған нүктенің мәні мына формуламен есептелінеді.

, (2.5)

Табылған нүктедегі функцияның мәні нөлге өте жуық болса, онда сол нүкте (2.1) теңдеудің түбірі, болмаса процесс жалғасады.

Егер түбірлер еселі болса, ол еселікті деп белгілейік.

. , (2.6)

Бақылау сұрақтары:

1. Сызықтық емес теңдеулердің неше түрі бар?

2. Алгебралық теңдеулер дегеніміз қандай теңдеулер?

3. Сызықтық емес теідеулерді шешудің неше сандық тәсілі бар?

4. Бір өлшемді сызықты емес теңдеуді шешудің қандай тәсілдерін білесіз?

Тақырыбы: Векторлар мен матрицалардың нормаларын есептеу және олардың қиюласуын теориялық және сандық шешу

Мақсаты: 3D StudioMax программасында жұмыс жасау

Тапсырма:

Берілген сызықты емес теңдеулер жүйелерінің түбірлерін Ньютон, Зейдель, қарапайым итерация әдістерімен анықтау.

№	Жүйелер	Қосымша шарт
		Y=0, y=x, x=0.5 түзулерімен шектелген облыстағы түбірлерін табу.
		Y=0, y=x, x=0.5 түзулерімен шектелген облыстағы түбірлерін табу.
		Y=0, y=x, x=0.5 түзулерімен шектелген облыстағы түбірлерін табу.
		Y=0, y=x, x=0.5 түзулерімен шектелген облыстағы түбірлерін табу.
		x>0, y>0, , k=0.1*m, m=0,1,2,3,4.
		x>0, y>0, , k=0.6+0.1*m, m=0,1,2,3,4.

Тапсырманы орындауға әдістемелік нұсқаулар:

Екі теңдеуден тұратын екі белгісізді сызықты емес теңдеулер жүйесін қарастырайық: (2.7)

Бұл есептің мақсаты - екі теңдеудің графигінің қиылысу нүктелерін анықтау.

Ньютон әдісі

Екі теңдеудің графигін сызып екеуінің қиылысу нүктелері жатқан облысты белгілейміз де осы облыстан жуықтап бастапқы жуықтауларды (x₀, y₀) таңдап аламыз ([3] қараңыз). Келесі жуықтауларды мына формулалармен есептейміз:

Мұндағы якобиан деп аталады.

Бұл әдіс бастапқы жуықтаулар түбірге жақын алынған уақытта тиімді.

Мысалы:

жүйесі берілген. Теңдеулердің графигін сызу (2-суретте.) арқылы бастапқы жуықтауларды табамыз

2-сурет. және функцияларының графиктері.

2-суреттен көріп отырғанымыздай, x₀=1.2; y₀=1.7 деп аламыз.

Якобианды есептейміз:

; n=0,1,2,..

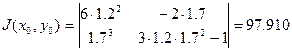
Ньютон формуласына қойсақ:

осылайша біртіндеп (х₂,у₂), (х₃,у₃),... жұптарының мәндерін F және G функцияларының мәні нөлге жуықтағанша есептейміз.

Қарапайым итерация әдісі

(2.7)-ші жүйе берілсін. Бұл әдісті қолданбас бұрын жүйені итерациялық түрге келтіріп алады: 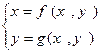(2.8)

Теңдеулердің графиктерін құру арқылы бастапқы жуықтауларды беріп, келесі жуықтауларды мына формуламен есептейді:

n=0,1,2,... (2.9)

Бұл әдістің жинақтылығын теореманың шарттарымен тексеру керек.

Теорема 1.4: Әлдебір тұйық облыста (2.7)-ші

жүйенің жалғыз шешімдері бар болсын: . Егер:

1) және функциялары облысында анықталған және үзіліссіз болса,

2) бастапқы және келесі жуықтаулардың барлығы осы облыста жатса,

3) осы облыста мына теңсіздіктер орындалса:

(2.10)

онда (2.8)-ші итерациялық процесс өзінің жалғыз шешіміне жинақталады, яғни , .

Қателігін бағалау:

. M=max(q1;q2).

Кей жағдайда (2.8)-ші итерациялық процестің орнына Зейдель процесін қолдануға болады:

n=0,1,2,... (2.11)

Жүйені итерациялық түрге келтіру

(2.7)-ші жүйені (2.8)-ші итерациялық түрге келтіру үшін келесі тәсілдерді қолданған дұрыс.

, болсын. (2.12)

Коэффициенттерді мына жүйеден табамыз:

(2.13)

Параметрлерді осылай таңдап алу арқылы (2.10)-ші шарттың орындалуын талап етуге болады.

: Берілген жүйе үшін итерациялық функцияларды таңдау.

х₀=0.8, y₀=0.55

Шешімді мына түрде іздейміз:

(2.14)

Коэффициенттерді анықтау үшін (2.13)-жүйе құруымыз керек, ол үшін дербес туындылардағы мәндерді есептейміз:

(2.15)

.

(2.15)-ті (2.13)-ке қойсақ:

(2.16)

(2.16)-ны шешеміз:

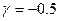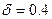, , , . Сонда .

Бұл мәндерді (2.14)-ші жүйеге қойсақ:

Есепті әрі қарай шешу үшін (2.9)-ші немесе (2.11)-ші итерациялық процесті құру керек.

Бақылау сұрақтары:

1. Итерацияның қарапайым әдісі қалай жүзеге асады?

2. Жүйе итерациялық түрге қалай келтіріледі?

3. Теңдеулер жүйесін шешуде Ньютон әдісі қалай жүзеге асады?

4. Сызықтық емес теңдеулер жүйесінің жазылуын көрсетіңіз?

Тақырыбы: Гаустың белгісізді біртіндеп жою әдісімен теңдеулер жиының сандық шешімін табу

Мақсаты: Сызықты алгебралық теңдеулер жүйесін шешудің сандық әдістерімен танысу және есептер шығару.

Тапсырма:

Гаусс әдісін қолданып төмендегі жүйелерді шешу.

№1 №2

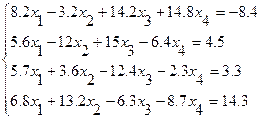
№3 №4

№5 №6

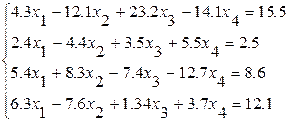
№ 7 №8

№ 9 №10

Тапсырманы орындауға әдістемелік нұсқаулар:

2. Гаусс әдісі.

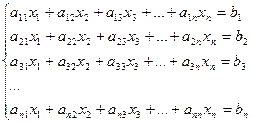(3.3)

(3.3) - квадрат матрицалы жүйе берілсін. Жүйенің матрицасы ерекше емес немесе айқындалмаған болсын. Гаусс әдісін практикада белгісіздерді біртіндеп жою әдісі деп те атайды.

Әдістің негізгі идеясы немесе мағынасы ([12],[13] қараңыз): берілген жүйенің матрицасын үшбұрышты түрге келтіру, бұл – тура жол деп аталады, сосын үшбұрышты матрицаны қолданып құрған жаңа жүйеден белгісіздерді біртіндеп табу, бұл – кері жол деп аталады. Сонда Гаусс әдісі 2 этаптан тұрады:

3. тура жол – матрицаны үшбұрышты түрге келтіру.

4. кері жол – белгісіздерді ең соңғысынан бастап кері қарай табу.

Бұл әдіс тура тәсілге жатады. Яғни белгісіздердің мәнін бастапқы жүйеге қойғанда теңдіктің оң жағындағы мәндер мен сол жағындағы мәндер бір біріне тең болады.

Матрицаны үшбұрышты түрге келтіру әр түрлі әдіспен орындалады, қолданылатын әдіс теңдеулердің коэффициенттеріне байланысты.

1. Тура жол:

басшы элементі нөлден өзгеше деп есептеп (3.3)- жүйенің бірінші теңдеуінің коэффициенттерін басшы элементке бөлу арқылы келесі теңдеуді аламыз:

(3.4.)

мұндағы , (3.5)

(3.4) - теңдеуді қолданып (3.3) - жүйенің 2-ші теңдеуінен, 3-ші теңдеуінен және n-ші теңдеуінен х₁ белгісізін жоюға болады. Ол үшін (3.4)-ші теңдеуді а₂₁, а₃₁,..., а_n1 коэффициенттеріне көбейтіп шыққан нәтижелерді сәйкесінше 2-ші теңдеуден, 3-ші теңдеуден, т.с.с. n-ші теңдеуден азайтып a_ij¹ деп белгілейміз:

(3.6)

Сонда келесідей жүйе аламыз:

(3.7)

Алынған (3.7) - жүйенің 1-ші теңдеуін а₂₂¹ элементіне бөліп, теңдеу аламыз:

(3.8)

мұндағы , (3.9)

х₁ белгісізін қалай жойсақ, тура сол сияқты х₂ белгісізін (3.7) - жүйеден жоямыз, сонда мынадай жүйе алынады:

(3.10)

мұндағы

(3.11)

(3.10) - жүйенің 1-ші теңдеуін элементіне бөліп

(3.11)

теңдеу аламыз. Мұндағы , (3.12)

(3.11) - теңдеу көмегімен (3.10) - жүйеден х₃ белгісізін жоямыз.

Осы әрекеттер тізімін матрица толық үшбұрышты түрге келгенше жалғастырамыз да (3.4)-ші, (3.8)-ші, (3.11)-ші, т.с.с. алуға болатын теңдеулерді жинақтап келесідей жүйе аламыз:

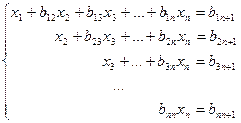(3.13)

2. Кері жол:

(3.13) - жүйенің ең соңғы n-ші теңдеуінен белгісізін тауып алып n-1 –ші теңдеуге қою арқылы x_n-1 белгісізін табуға, сол сияқты кері қарай барлық белгісіздерді табуға болады.

Ескерту: Бұл әдіс матрицаның басшы элементі нөлден өзгеше болған жағдайда қолданылады. Егер берілген жүйе матрицасының басшы элементі нөлге тең болса, жүйенің теңдеулерінің орындарын ауыстыру арқылы, арифметикалық операциялар қолдану арқылы басшы элементтің нөлдігінен құтылуға болады.

Практикада есептеу жеңіл болуы үшін Гаусс компактілі схемасын толтырады (1-кесте), мысал үшін 4 белгісізді жүйе қарастырылды.

1-мысал:

(3.14)

Есептеу процесінің қалай өрбитінін бақылау үшін кесте толтырған дұрыс (2-кестені қараңыз). Кестенің I - бөлігіне жүйенің кеңейтілген матрицасын толтырамыз.

Кестенің соңғы екі бағаны ∑, S – есептеу қателігін бақылауды ұйымдастырады. I – бөліктің ең соңғы бақылаушы бағанындағы мәндер матрицаның әр жолындағы элементтердің қосындысы ретінде табылады 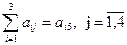. b_1j жолының бақылаушы бағанындағы элементтер I – бөліктің ең соңғы бақылаушы бағанындағы мәндерді басшы элементке бөлу арқылы табылады . II – бөліктің бақылаушы бағанындағы мәндер I – бөліктің ең соңғы бақылаушы бағанындағы мәндерге (3.6) - формуланы қолдану арқылы анықталады . Дәл осылай бақылаушы бағанның қалған екі жолын да толтыруға болады:

, төменде көрсетілген , формулалары арқылы. ∑, S – бағандарындағы мәндер бір - бірінен өте аз ауытқуы немесе тұтас беттесуі керек. Сонда есеп дұрыс жүргізілген болады.

(3.5) - формуланы қолданамыз:

1-кесте. Гаусстың компактілі схемасы.

Бөліктер	i	X1	X2	X3	X4	bi	∑=ai6
I		a11   a21   a31   a41	a12   a22   a32   a42	a13   a23   a33   a43	a14   a24   a34   a44	b1   b2   b3   b4
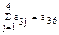
B1j			b12	b13	b14	b15
II
B2j				b23	b24	b25
III
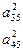
B3j					b34	b35
IV
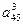
V						x4 x3 x2 x1

; ; ;

;

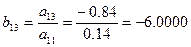Бұл мәндерді кестенің b_1j жолына жазамыз.

(3.6) - формуланы қолданамыз:

;

;

; Бұл сандарды кестенің II – бөлігіндегі сәйкес орындарына жазамыз.

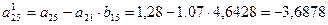(Бұл мән кестенің ∑ бағанында орналасады.)

Дата добавления: 2017-01-14