Гаусстыњ квадратуралыќ формулалары. 2 страница

L₁³(x) мүшесін есептемейміз, себебі y₁=0. Бәрін бір біріне қосамыз да көпмүшеліктің соңғы түрін аламыз:

(4.9)

2-мысал: Кесте мен берілген функцияның x=0.45 нүктесіндегі мәнін анықтау керек.

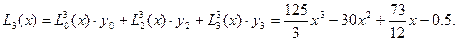
X	0.05	0.15	0.20	0.25	0.35	0.40	0.50	0.55
y	0.9512	0.8607	0.8187	0.7788	0.7047	0.6703	0.6065	0.5769

Шешімі:

Есептеуді жеңілдету үшін x=0.05t деп алайық. X-тердің мәні белгілі болғанда t-лардың мәндерін тауып алуға болады, олар: 1, 3, 4, 5, 7, 8, 10, 11. Және x=0.45 болғандағы t=9 болады. Есептеу қадамдары 2-кесте да келтірілген.

2-кесте. (4.9)-есептің есептелу қадамдары.

i	ti-tj (i<>j)	Di	yi
		-2	-3	-4	-6	-7	-8	-10	-725 760	0.9512	-0.0131*10^-4
			-1	-2	-4	-5	-7	-8	26 880	0.8607	0.3202*10^-4
				-1	-3	-4	-6	-7	-7 560	0.8187	-1.0829*10^-4
					-2	-3	-5	-6	5 760	0.7788	1.3520*10^-4
						-1	-3	-4	-3 456	0.7047	-2.0390*10^-4
							-2	-3	2 520	0.6703	2.6599*10^-4
							-1	-1	11 340	0.6065	0.5348*10^-4
								-2	-80 640	0.5769	-0.0715*10^-4

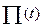
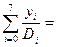
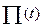
Сонымен y(0.45)= 3840*1.6604*10^-4=0.6376.

Егер есепте керісінше функция мәні белгілі болып сол мәнге сәйкес абсцисса мәнін табу керек болса, ондай есепті кері интерполяциялау деп атайды. Кері интерполяциялау формуласы:

(4.10)

Ньютоннның интерполяциялық формулалары

Егер интерполяциялық түйіндердің бір бірінен ара қашықтығы тұрақты болса, практикада Ньютонның интерполяциялық формулалары қолданылады. Бұл формулалар екіге бөлінеді:

1. Алдыға қарай интерполяциялау
2. Кері интерполяциялау

Егер берілген х нүктесінің мәні кестенің бас жағында жатса, 1-формуласы қолданылады:

(4.11)

.

Мұндағы

Егер берілген х нүктесінің мәні кестенің соңғы жағянда жатса, 2-формула қолданылады:

(4.12)

Формулалардағы 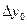, , 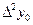т.с. сияқтылар шектік айырымдар деп аталады және 3-кестені толтыру арқылы анықталады. Кестедегі мысал үшін 6 интерполяциялық түйін және шектік айырымдардың 4-ші дәрежесіне дейінгі мәндер қарастырылған. 1-формула үшін кестенің бірінші жолындағы мәндер, 2-формула үшін кестенің соңғы жолындағы мәндер қолданылады.

3-кесте. Шектік айырымдар кестесі.

x	Y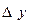
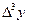
X0	Y0
X1	Y1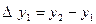
X2	Y2
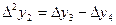
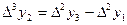
X3	Y3
X4	Y4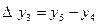
X5	Y5

Егер интерполяциялық түйіндер саны 1 немесе 2-ге тең болса сызықты интерполяциялық формуланы қолдануға болады: .

Қателіктерін бағалау:

1-формула үшін мына формула қолданылады:

,

немесе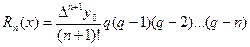

2-формула үшін мына формула қолданылады:

,

Мысал: y=lg(x) функциясының мәндері кесте да берілген, lg1001 мәнін табу керек.

4-кесте. y=lg(x) функциясының мәндері және

шектік айырымдары кестесі

x	Y
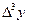
	3.0000000	43 214	-426
	3.0043214	42 788	-418
	3.0086002	42 370	-409
	3.0128372	41 961	-401
	3.0170333	41 560
	3.0211893

3-ретті шектік айырымдар тұрақты бола бастағандықтан кесте ны толтыруды тоқтатамыз. Формулада n=3 деп аламыз. Q=0,1. x=1001. Ньютонның бірінші формуласын қолданамыз, себебі х-тің мәні кестенің бас жағында жатыр, сонда lg1001=3.00043417+0.5*10^-9 болатынын қалдық мүшенің формуласын қолдану арқылы анықтаймыз.

Бақылау сұрақтары:

1. Лагранждың интерполяциялық көпмүшелігі?

2. Эйткен схемасы?

3. Ньютоннның интерполяциялық формулалары?

4. Шектік айырымдар кестесі қалай есептеледі?

Тақырыбы: Гаусс квадратурасын қолданып, Рунге принципінің негізінде интегралды есептеу

Мақсаты: Функцияны интерполяциялау есептерін шығаруды үйрену

Тапсырма:

E=10^-5 дєлдікпен тµмендегі интегралдарды сєйкес єдісті тањдау арќылы есептеңіздер.

1. ;

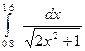2.

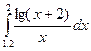
3.

4.

5.

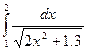
6.

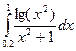
7.

8.

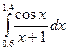
9.

10.

11.

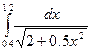
12.

13.

14.

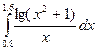
15. , аралыќты 2-ге бµлу арќылы есептеу.

16.

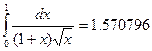
17.

18.

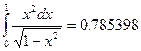
19.

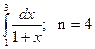
20.

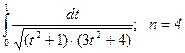
Тапсырманы орындауға әдістемелік нұсқаулар:

Канторовичтің интеграл астындағы функцияның ерекшелігін айшыќтау әдісі.

Б±л єдістіњ негізгі идеясы f(x) функциясынан єлдебір g(x) функциясын бµліп алады да f(x)-g(x) айырымынан интеграл алады, м±ндаѓы f(x)-элементарлы интегралданатын болуы керек, ал g(x) – сандыќ єдістердіњ біреуімен интегралданатын болуы керек:

(5.7)

Б±л єдіс интеграл астындаѓы функция келесі т‰рде берілген жаѓдайда ќолданылады:

М±ндаѓы 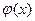функциясы [a,b] аралыѓында ‰зіліссіз дифференциалданатын функция болсын. Онда б±л функцияны Тейлор ќатарына жіктеуге болады. Тейлор ќатарына жіктелген функция т‰рін деп белгілесек:

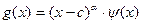болады. Сонда айырманы 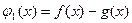деп ќарастыруѓа болады.

Мысалы: ;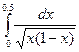

Интеграл астындаѓы функияны келесі т‰рде жазып алуѓа болады:

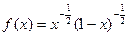. Онда 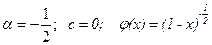болады. Б±л функцияны Тейлор ќатарына жіктеуге болады:

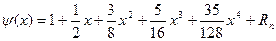. Онда: 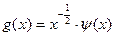, 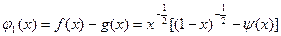болады.

Дәрежелік ќатарлар кµмегімен интегралдау єдісі.

Интеграл астындаѓы функция [a,b] аралыѓы жатќан (-R,+R) интервалында жинаќталатын дєрежелік ќатарѓа жіктелетін болсын:

(5.8)

Дєрежелік ќатарды м‰шелеп интегралдауѓа болады, сонда:

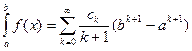(5.9)

Егер (5.9)-ќатар жинаќты болса, онда 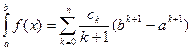(5.10)

Єдіс ќателігі ќатар ќалдыѓы мен дµњгелектеу ќателігінен т±рады.

Егер ќатардыњ тањбасы ауыспалы жєне абсолютті шамасы бойынша монотонды кемімелі болса, онда ќатар ќалдыѓы тасталатын (отбрасываемый) ќатар м‰шелерініњ ењ біріншісініњ абсолют ќателігінен аспайды.

Басќа жаѓдайларда ќатар ќалдыѓын баѓалау ‰шін ќатарлары жењіл баѓаланатын сандыќ ќатарлармен мажорлайды.

Мысал:

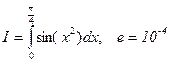
Интеграл астындаѓы функция дєрежелік ќатарѓа жіктеледі жєне кез келген х ‰шін жинаќталады:

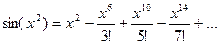
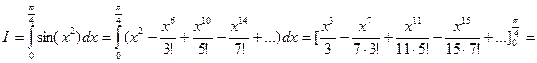
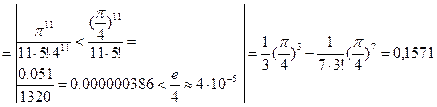
Ќатардыњ ‰шінші м‰шесінен бастап ќалѓан м‰шелерін тастап кетуге болады, себебі олар нµлге µте жуыќ.

Б±л єдісте х айнымалысын µрнекпен алмастырады: 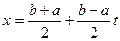. Сонда Гаусс формуласы былай жазылады:

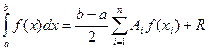(5.11)

м±ндаѓы , ал ,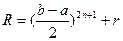

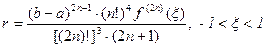
Б±л єдістіњ ыњѓайсыздыѓы, абсциссадаѓы мєндер мен коэффициенттер иррационал сандар. Біраќ соѓан ќарамай интегралдау т‰йіндерініњ саны аз болса да, дєлдігі жоѓары.

Абсциссадаѓы мєндер мен коэффиценттер м‰мкін, жоѓары дєрежелі кµпм‰шеліктердіњ барлыѓы ‰шін (5.11)-формула д±рыс болатындай етіп тањдалынып алуы керек. 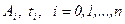сандары N=2n-1 болѓанда бірмєнді болатыны дєлелденген.

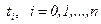мєндерін аныќтау ‰шін Лежандр кµпм‰шелігі ќолданылады:

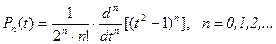
Ал 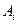-лерді табу ‰шін тµмендегі ж‰йе шешіледі:

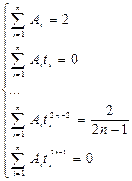(5.11.1^’)

Б±л ж‰йені шешу барысында коэффициенттерді тµмендегі 1-кесте кµмегімен де аныќтауѓа болады.

1-кесте. (5.11.1^’)-жүйені шешу барысында анықталған коэффициенттер.

n	I	ti	Ai
	1;2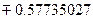
	1;3
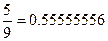
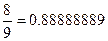
	1;4 2;3		0.34785484 0.65214516
	1;5 2;4		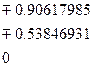0.23692688 0.47862868 0.56888889

Мысалы:

N=5 болѓанда интегралын Гаусс формуласымен есептеу керек болсын. Айнымалыны ауыстырамыз: 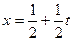. Сонда интеграл мына т‰рге келеді:

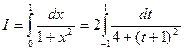; (5.12)

;

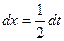x=0 болѓанда t=-1;

x=1 болѓанда t=1;

Интеграл астындаѓы функцияныњ мєндер кесте сын ќ±рамыз:

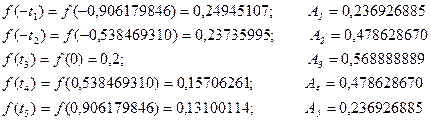
Алынѓан мєндерді (4)-ќою арќылы интегралды есептейміз:

.

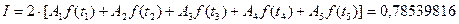Дата добавления: 2017-01-14