
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Гаусстыњ квадратуралыќ формулалары. 1 страница
|
|
|
|
Мысал
Кері жол
Тура жол
Кері жол алгоритмі
Басшы жолдардан құралған матрицаны әлдебір ауыстырулар арқылы үшбұрышты түрге келтіріп, ең соңғы теңдеуден ең соңғы белгісізді, оны қолданып оның алдындағы белгісізді, т.с.с. барлық белгісіздерді кері бағытта анықтаймыз.
 сандары қаншалықты азайған сайын есептеу қателігі де азаяды. Сондықтан ЭЕМ-ді қолданып есептеу уақытында осы әдіс тиімді деп есептеледі.
сандары қаншалықты азайған сайын есептеу қателігі де азаяды. Сондықтан ЭЕМ-ді қолданып есептеу уақытында осы әдіс тиімді деп есептеледі.
Ескерту. Егер жүйе өте көп белгісіздерден тұрып, оның барлық элементтерінің арасынан модулі бойынша үлкен элементті табу қиынға соқса басшы жол ретінде жүйенің бірінші жолын, ал басшы элемент ретінде осы жолдың модулі бойынша ең үлкен элементін алуға болады.
2-мысал:
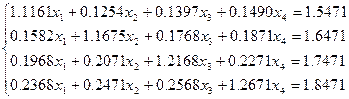 (3.18)
(3.18)
Есептеу қадамдарының нәтижелерін 3- кестеге толтыруға болады:
3- кесте. (3.18) – есептің кестелік алгоритмі.
| Бөліктер | I | mi | X1 | X2 | X3 | X4 | Ai5 |
| I | 0.11759 0.14766 0.17923 | 1.1161 0.1582 0.1968 0.2368 | 0.1254 1.1675 0.2071 0.2471 | 0.1397 0.1768 1.2168 0.2568 | 0.1490 0.1871 0.2271 1.2671 | 1.5471 1.6471 1.7471 1.8471 | |
| II | 0.09353 0.11862 | 1.08825 0.12323 0.15436 | 0.09634 1.13101 0.16281 | 0.10950 0.13888 1.177077 | 1.32990 1.37436 1.41604 | ||
| III | 0.07296 | 1.07381 0.10492 | 0.08111 1.11170 | 1.19746 1.20639 | |||
| IV | 1.06616 | 1.10944 |
а44=1,2671 басшы элемент болады. 4-жол басшы жол деп аталады.
1. (3.16) - формула көмегімен mi, i=1,2,3 мәндерін анықтаймыз:
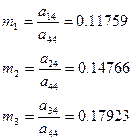
2. (3.17) – формула бойынша басшы бағанда орналасқан басшы элементтен өзге элементтерді нөлге айналдырамыз да қалған жаңа элементтерді табамыз:
i=1; j=1 болғанда

i=1; j=2 болғанда

i=1; j=3 болғанда
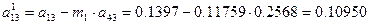
i=1; j=4 болғанда

i=1; j=5 болғанда
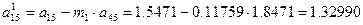
i=2; j=1 болғанда

i=2; j=2 болғанда
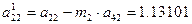
i=2; j=3 болғанда
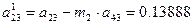
i=2; j=4 болғанда

i=2; j=5 болғанда

i=3; j=1 болғанда

i=3; j=2 болғанда
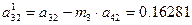
i=3; j=3 болғанда

i=3; j=4 болғанда
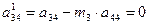
i=3; j=5 болғанда

Табылған элементтерден жаңа матрица құрып кестенің II-бөлігіне толтырамыз.
3. Жаңа матрицадан модулі бойынша үлкен элементті табамыз: ол -  . 3-жолды басшы жол деп аламыз да жаңа көбейткіштерді анықтаймыз:
. 3-жолды басшы жол деп аламыз да жаңа көбейткіштерді анықтаймыз:

4. 2-пункттегі сияқты (3.17) – формула бойынша басшы бағанда орналасқан басшы элементтен өзге элементтерді нөлге айналдырамыз да қалған жаңа элементтерді тауып тағы жаңа матрица құраймыз:
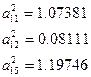

5. Осы жаңа матрицадан модулі бойынша үлкені  . Тағы көбейткішті есептейміз:
. Тағы көбейткішті есептейміз:  .
.
6. 2-пункттегі сияқты (3.17) – формула бойынша басшы бағанда орналасқан басшы элементтен өзге элементтерді нөлге айналдырамыз да қалған жаңа элементтерді тауып тағы жаңа матрица құраймыз:
 ;
; 
Кесте да қоршалған басшы элементтер орналасқан жолдардан жүйе құрамыз:
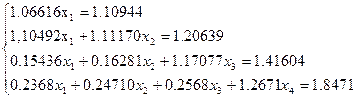
Белгісіздерді біртіндеп табамыз:
X1=1.04059
X2=0.98697
X3=0.93505
X4=0.88130.
Квадрат түбірлер әдісі.
 (3.19)
(3.19)
Жүйенің матрицасы симметриялы элементтерден тұратын болса, онда мұндай жүйеге квадрат түбірлер әдісі қолданылады. Әдістің мақсаты ([13] қараңыз) берілген матрицаны бір-біріне түйіндес екі үшбұрыш матрицаның көбейтіндісі түріне келтірейік.
A=S*DS (3.20)
мұндағы S*- төменгі үшбұрышты матрица, S- жоғарғы үшбұрышты матрица.
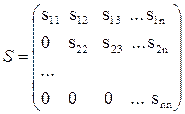
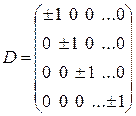
SS*D матрицасын бір-біріне көбейтіп элементтерін А матрицасының элементтеріне теңестіреміз. Алынған матрицасының диоганалдық элементтері мына формуламен есептелінеді.

ал қалған элементтер үшін мына формула қолданылады:


 (3.21)
(3.21)
 (3.22)
(3.22)
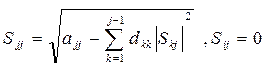 (3.23)
(3.23)
 (3.24)
(3.24)
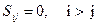 (3.25)
(3.25)
Егер берілген матрицаның коэффициенті нақты және бас минорлары оң болса, онда d матрицасын бірлік матрица деп, есептеу мына фолмулалармен жүргізіледі:
 (3.21*)
(3.21*)
 (3.22*)
(3.22*)
 (3.23*)
(3.23*)
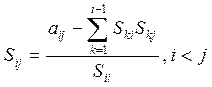 (3. 24*)
(3. 24*)
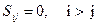 (3.25*)
(3.25*)
Бұл формулаларды қолданғаннан кейін шыққан матрицаны мынадай үшбұрышты жүйе құрамыз:
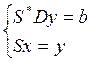 (3.26)
(3.26)
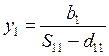 (3.27)
(3.27)
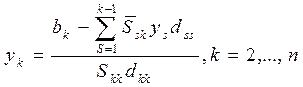 (3.28)
(3.28)
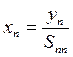 (3.29)
(3.29)

 (3.30)
(3.30)
Практикада бұл әдіс мына 4-кестені толтырады.
4-кесте. Квадрат түбірлер әдісінің схемасы.
| i | x1 | x2 | x3 | bi |
| A11 | a12 | a13 | b1 | |
| A21 | a22 | a23 | b2 | |
| A31 | a32 | a33 | b3 | |
| У1 | У2 | У3 | bi | |
 11 11
| b1 | |||
 12 12
|  22 22
| b2 | ||
 13 13
|  23 23
|  33 33
| b3 | |
| x1 | x2 | x3 | yi | |
| S11 | S21 | S31 | y1 | |
| S22 | S32 | y2 | ||
| S33 | y3 |

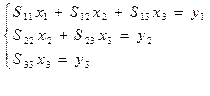 немесе матрицалық –векторлық түрде:
немесе матрицалық –векторлық түрде:
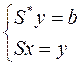 .
.
Ал үшбұрышты түрге келтірілген жүйенің белгісіздері қарапайым табылады.

e=0.5*10-3
Жүйе симметриялы элементтерден тұрады, яғни квадрат түрбірлер әдісін қолдануға болады:
(3.21*) - формула бойынша:
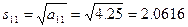
(3.22*)-формула бойынша: 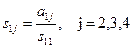

(3.23*) - формула бойынша:  j=2,3 формуласы бойынша диагональдық элементтерді табамыз:
j=2,3 формуласы бойынша диагональдық элементтерді табамыз:

s23 элементі әлі табылған жоқ, сондықтан мына формуланы қолданып тауып аламыз:
(3.24*) - формула бойынша: 
 . Енді (3.21*) - формуламен s33-ті табуға болады:
. Енді (3.21*) - формуламен s33-ті табуға болады:
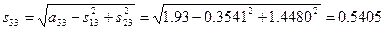
Енді (3.21*) - формуламен қалған элементтерді табамыз:
 =у2 деп белгілейміз
=у2 деп белгілейміз
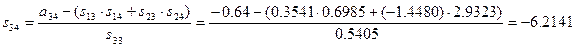 = у3 деп белгілейміз
= у3 деп белгілейміз
Енді элементтерден S үшбұрышты матрица құраймыз:
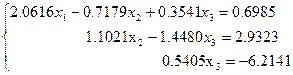
Бұдан 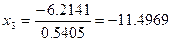 .
. 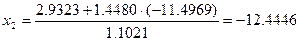
Бақылау сұрақтары:
1. Сызықты алгебралық теңдеулер жүйесін (САТЖ) сандық шешудің неше тәсілі бар?
2. Гаусс әдісі қалай жүзеге асады?
3. Жордан – Гаусс әдісі қалай жүзеге асады?
4. Жордан – Гаусс әдісінің тура әдісі қалай жүзеге асады?
Тақырыбы: Бір айнымалы функцияны кубтық сплайнмен интерполяциялау
Мақсаты: Функцияны интерполяциялау есептерін шығаруды үйрену
Тапсырма:
Тапсырма:
1. Функцияның мәндер кестесі берілген:
| Х | 1,50 | 1,54 | 1,56 | 1,60 | 1,63 | 1,70 |
| У | 3,873 | 3,924 | 3,950 | 4,000 | 4,037 | 4,123 |
Лагранж формуласын қолданып көрсетілген нүктелердегі функция мәндерін анықтау:
a) 1,52 b) 1,55 c) 1,58 d) 1,61 e) 1,67.
2. Функцияның мәндер кестесі берілген:
| Х | 2,0 | 2,3 | 2,5 | 3,0 | 3,5 | 3,8 | 4,0 |
| У | 5,848 | 6,127 | 6,300 | 6,694 | 7,047 | 7,243 | 7,368 |
Лагранж формуласын қолданып көрсетілген нүктелердегі функция мәндерін анықтау:
a) 2,22 b) 2,41 c) 2,78 d) 3,34 e) 3,75, f) 3,88.
3. sin(x) функциясының x=0,  /6,
/6,  /4
/4  /3
/3  /2 нүктелеріндегі мәндерін біле отырып x=
/2 нүктелеріндегі мәндерін біле отырып x=  /12 нүктесіндегі мәнін және қателігін анықтау.
/12 нүктесіндегі мәнін және қателігін анықтау.
4. Cos(x) функциясының x=0,  /6,
/6,  /4
/4  /3
/3  /2 нүктелеріндегі мәндерін біле отырып x=
/2 нүктелеріндегі мәндерін біле отырып x=  /5 нүктесіндегі мәнін және қателігін анықтау.
/5 нүктесіндегі мәнін және қателігін анықтау.
5. Эйткен схемасын бойынша кестеде берілген функция мәндерін қолданып, берілген нүктелердегі функция мәндерін есептеу:
a) y(27).
| Х | ||||
| У | 68,7 | 64,0 | 44,0 | 39,1 |
b) Y(102).
| Х | 93.0 | 96.2 | 100.0 | 104.2 | 108.7 |
| У | 11.38 | 12.80 | 14.70 | 17.07 | 19.91 |
c) Y(5).
| Х | ||||||
| У | 658 503 | 704 969 | 729 000 | 804 357 | 830 584 | 884 736 |
4.Кесте түрінде берілген функция үшін Эйткен схемасын қолданып 10-5 дәрежесі дәлдікке дейін х-тің берілген мәндеріндегі функция мәндерін анықтау:
| Х | 1,00 | 1,08 | 1,13 | 1,20 | 1,27 | 1,31 | 1,38 |
| У | 1,17520 | 1,30254 | 1,38631 | 1,50946 | 1,21730 | 1,22361 | 1,23470 |
a) 1,134 b) 1,139 c) 1,143 d) 1,151 e) 1,166 f) 1,175 g) 1,182 i) 1,197
k) 1,185 l) 1,192 m) 1,195.
6. Функцияның берілген кестелік мәндер бойынша берілген функция мәніне сәйкес аргумент мәнін анықтау:
a) y=0
| Х | 2,5 | |||
| У | -6 | -1 | 5,625 |
b) y=20
| X | ||||
| Y |
c) y=2.00139; y=2.00194; y=2.00373; y=2.00484
| X | 1.00 | 1.05 | 1.10 | 1.15 | 1.20 | 1.25 |
| Y | 2.00000 | 2.00238 | 2.00909 | 2.01957 | 2.03313 | 2.05000 |
1. y=ex функциясының мәндері кестемен берілген. Сызықты интерполяциялау формуласын қолданып функцияның берілген нүктелердегі мәндерін анықтау.
| x | 0.50 | 0.51 | 0.52 | 0.53 | 0.54 | 0.55 | 0.56 | 0.57 | 0.58 | 0.59 | 0.60 |
| ex | 1.6487 | 1.6653 | 1.6820 | 1.6989 | 1.7160 | 1.7333 | 1.7507 | 1.7683 | 1.7860 | 1.8040 | 1.8221 |
|
2. y=sin(x) функциясының мәндері берілген. Ньютонның сәйкес формуласын қолдану арқылы берілген нүктелердегі мәндерді және қателіктерін анықтау.
| X | 1.1 | 1.2 | 1.3 | 1.4 | 1.5 | 1.6 | 1.7 |
| Sin(x) | 0.89121 | 0.93204 | 0.96356 | 0.98545 | 0.99749 | 0.999957 | 0.99166 |
| 1.8 | 1.9 | 2.0 | 2.1 | 2.2 | 2.3 | 2.4 | 2.5 |
| 0.97385 | 0.94630 | 0.90930 | 0.86321 | 0.80850 | 0.74571 | 0.67546 | 0.59847 |
|
3. f(x) функциясының мәндері кестемен берілген. Көрсетілген нүктелердегі функция мәндерін Ньютонның формулаларымен анықтау.
| X | 1.50 | 1.51 | 1.52 | 1.53 | 1.54 | 1.55 | 1.56 | 1.57 | 1.58 | 1.59 | 1.60 |
| F(x) | 0.51183 | 0.50624 | 0.50064 | 0.49503 | 0.48940 | 0.48376 | 0.47811 | 0.47245 | 0.46678 | 0.46110 | 0.45540 |
|
4. g(x) функциясының мәндері кестемен берілген. Көрсетілген нүктелердегі функция мәндерін Ньютонның формулаларымен анықтау.
| x | 1.0 | 1.1 | 1.2 | 1.3 | 1.4 | 1.5 | 1.6 | 1.7 | 1.8 | 1.9 | 2.0 |
| g(x) | 0.5652 | 0.6375 | 0.7147 | 0.7973 | 0.8861 | 0.9817 | 1.0848 | 1.1964 | 1.3172 | 1.4482 | 1.5906 |
|
5. h(x) функциясының мәндері кестемен берілген. Көрсетілген нүктелердегі функция мәндерін Ньютонның формулаларымен анықтау.
|
| x | 0.00 | 0.05 | 0.10 | 0.15 | 0.20 | 0.25 | 0.30 | 0.35 | 0.40 | 0.45 | 0.50 |
| h(x) | 0.28081 | 0.31270 | 0.34549 | 0.37904 | 0.41318 | 0.44774 | 0.48255 | 0.51745 | 0.55226 | 0.58682 | 0.62096 |
Тапсырманы орындауға әдістемелік нұсқаулар:
Лагранждың интерполяциялық көпмүшелігі.
 (4.4)
(4.4)
Кей жағдайда есептеу процесін жеңілдету үшін x=at+b, xj=atj+b j=0,1,…,n сызықты алмастыруын жасау арқылы Лагранж коэффициенттерінің инварианттылығын қолдануға болады, онда (4.4)-формула келесі түрге келеді:
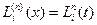 (4.5)
(4.5)
Эйткен схемасы.
Егер Лагранж көпмүшелігінің жалпы өрнегін анықтамай, тек белгілі бір нүктедегі функция мәнін есептеу керек болса, онда Эйткен схемасын қолдануға болады:


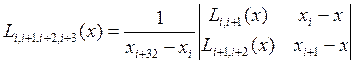 т.с.с. (4.6)
т.с.с. (4.6)
Эйткен схемасы келесі 1-кестені толтыру арқылы орындалады.
1-кесте. Эйткен схемасының толтырылу кестесі
| xi | yi | Xi-x | Li-1,i | Li-2,i-1,i | Li-3,i-2,i-1,i | … |
| X0 | Y0 | X0-x | ||||
| X1 | Y1 | X1-x | L01(x) | |||
| X2 | Y2 | X2-x | L12(x) | L012(x) | ||
| X3 | Y3 | X3-x | L23(x) | L123(x) | L0123(x) | … |
| X4 | Y4 | X4-x | L34(x) | L234(x) | L1234(x) | … |
Эйткен схемасын есептеуді көршілес L0123…n(x), L0123…n,n+1(x) мәндері берілген дәлдік маңайында бір бірімен беттессе тоқтатуға болады.
Xi нүктелерінде yi мәндерін қабылдайтын n-ші дәрежелі интерполяциялық көпмүшелік келсі түрде де жазылады:
 . (4.7)
. (4.7)
1-Мысал: Кестемен берілген функция үшін Лагранж көпмүшелігін құру.
| I |
| |||||
| xi | 0.1 | 0.3 | 0.5 | |||
| yi | -0.5 | 0.2 |
Шешімі: (4.4)-формула бойынша n=3, i=0,1,2,3 болғандағы өрнекті анықтаймыз:
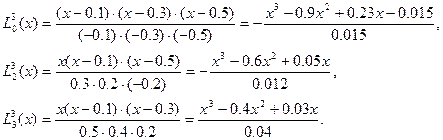
|
|
|
|
|
Дата добавления: 2017-01-14; Просмотров: 732; Нарушение авторских прав?; Мы поможем в написании вашей работы!