Основные функции состояния рабочего тела

Газовые смеси

Под газовой смесью понимается смесь газов, не вступающих между собой в химические реакции. Составляющие смесь отдельные газыназываются компонентами. Каждый компонент смеси распространяетсяпо всему объему смеси.

Давление, которое имел бы каждый компонент, входящий в состав смеси, если бы он находился один в том же объеме и при той же температуре, что и смесь, называется парциальным давлением компонента (от латинского pars – часть).

По закону Дальтона давление смеси равно сумме парциальных давлений ее компонентов, т. е.:

P_см = P₁ + P₂ + P₃ +... + P_n = , (5.13)

где Р_см – давление газовой смеси; Р₁, Р₂, Р₃, Р_n – парциальные давления компонентов смеси.

Итак, каждый компонент смеси, занимая весь объем смеси, находится под своим парциальным давлением. Но если этот компонент поместитьпод давлением Р_см при той же температуре смеси T_см, то он займет объемV_i меньший, чем объем V_см. Этот объем V_i называют приведенным илипарциальным.

Объем смеси равен сумме парциальных объемов ее компонентов:

V = V₁ + V₂ + V₃ + … + V_n= , (5.14)

где V – полный объем смеси газов, м³; V₁, V₂, V₃,…,V_n – парциальныеобъемы компонентов,м³, приведенные к условиям смеси, т. е. Р_см и Т_см.

Состав газовой смеси чаще всего задается массовым или объемным способом.

Массовая доля определяется отношением массы отдельного газа, входящего в смесь, к массе всей смеси:

где М₁, М₂, М₃, …, М_n - масса отдельных газов, кг и М – масса всей смеси, кг.

Объемной долей газа называют отношение объема каждого компонента, входящего в смесь, к объему всей газовой смеси при условии, что объем каждого компонента отнесен к давлению и температуре смеси (приведенный объем):

где V₁, V₂, V₃, …, V_n– приведенные объемы компонентов газов, входящих в смесь,м³;V – общий объем газовой смеси, м³.

Очевидно, что:

M₁+M₂+M₃+…+M_n = M,

m₁+m₂+m₃+…+m_n = 1,

а также:

V₁+V₂+V₃+…+V_n= V,

r₁+r₂+r₃+…+r_n = 1.

Для перевода массовых долей в объемные пользуются формулой:

(5.15)

Перевод объемных долей в массовые производится по формуле:

. (5.16)

Плотность смеси определяется из выражения:

(5.17)

или, если известен массовый состав, по формуле:

, кг/м³. (5.18)

Удельный объем смеси представляет величину, обратную ρ_см, поэтому, если дан объемный состав смеси, то:

(5.19)

Если же известен массовый состав, то:

(5.20)

Из уравнения (5.17) легко получается значение так называемой кажущейся молекулярной массы газовой смеси:

, (5.21)

или через массовый состав:

(5.22)

Таблица 5.2.

Формулы для расчёта газовых смесей

Задание состава смеси	Перевод из одного состава в другой	Плотность и удельный объем смеси	Кажущаяся молекулярная масса смеси	Газовая постоянная смеси	Парциальное давление
Массовыми долями
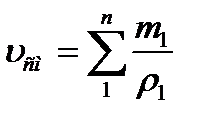
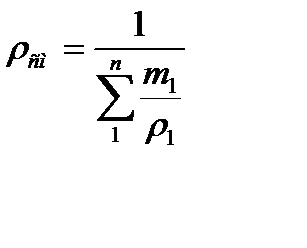
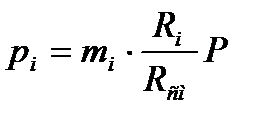
Объемными долями

Газовую постоянную смеси газов (R_см) можно выразить либо через газовые постоянные отдельных компонентов, входящих в смесь, либо через кажущуюся молекулярную массу смеси:

(5.23)

или:

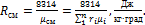(5.24)

Связь между давлением газовой смеси и парциальными давлениями отдельных компонентов, входящих в смесь, устанавливается следующей зависимостью (закон Дальтона), легко получаемой из основного уравнения кинетической теории газов:

, (1.25)

где P – общее давление газовой смеси;p₁, p₂, …, p_n – парциальные давления отдельных компонентов, входящих в смесь.

Парциальные давления определяются проще всего, если известны объемные доли отдельных компонентов, входящих в смесь:

,

или вообще:

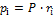. (1.26)

где p_i – парциальное давление любого газа, входящего в смесь.

В табл. 1.2 дана сводка формул, применяемых при расчетах газовых смесей.

1.3. Теплоёмкость газов

Теплоемкостью (точнее удельной теплоемкостью) называют количество теплоты, которое необходимо сообщить телу (газу), чтобы изменить температуру какой-либо количественной единицы на 1°С (1К).

Количество теплоты в системе СИ измеряют в Дж или кДж. В зависимости от количественной единицы вещества различают массовую теплоемкость С – кДж/(кг·К), объемную теплоемкость С’–кДж/(м³·К) и киломольнуютеплоемкостьμС– кДж/(кмоль·К).

Поскольку в 1 м³ в зависимости от параметров состояния содержится различная масса газа, то объемную теплоемкость всегда относят к 1 м³ газа при нормальных условиях (Р_Н = 760 мм рт. ст., t_Н = 0°С).

Массовая, киломольная и объемная теплоемкости связаны между собой следующими зависимостями:

(1.27)

где μ– молекулярная масса или количество кг в киломоле данного вещества, кг/кмоль;

(1.28)

где 22,4 – объем киломоля любого идеального газа в нормальных физических условиях (следствие из закона Авогадро), м³_н /кмоль;

C’= С·ρ_н, (1.29)

где ρ_Н – плотность данного вещества при нормальных условиях, кг/м³_н.

Теплоемкость идеальных газов зависит от атомности, характера процесса и температуры.

Теплоемкость реальных газов, кроме перечисленных выше факторов, зависит еще и от давления. Зависимость теплоемкости от температуры обычно выражают формулой:

C= a+ bt+ et², (1.30)

где t–температура в°С; a, b, е–численные коэффициенты, определяемые экспериментально.

Аналогичные зависимости получены не только для массовых, но и для других видов теплоемкости (объемных, киломольных).

Различают среднюю и истиннуютеплоемкости.

Средняятеплоемкость в интервале температур t₁ – t₂ равна:

, (1.31)

где q_1-2 – количество теплоты, подведенное в данном процессе, кДж/кг;

t₁, t₂ – температура в начале и в конце процесса, °С.

Если выражение (1.31) записать для бесконечно малого количества теплоты dq и интервала температур dt, то получим формулу так называемой истинной теплоемкости С при данной температуре:

. (1.32)

Из выражения (1.32) dq = Cdt, а для всего процесса 1–2 количество теплоты q_1-2 будет равно:

. (1.33)

Это же количество теплоты можно выразить через среднюю теплоемкость, что следует из (1.31):

. (1.34)

Имеется еще одна формула для подсчета q_1-2:

. (1.35)

Применение этого выражения удобно при наличии таблиц средних теплоемкостей .

В некоторых случаях требуется, пользуясь таблицами средних теплоемкостей , определить значение теплоемкости . Для этого из(1.34) и (1.35) можно получить формулу:

. (1.36)

В теплотехнике особое значение имеют два случая нагревания (охлаждения): при постоянном давлении (изобарный процесс) и припостоянном объеме (изохорный процесс). Обоим этим случаямсоответствуют изобарные и изохорные теплоемкости, имеющие вобозначениях индексы «p» «v».

Изобарные теплоемкости:

Изохорные теплоемкости:

Между теплоемкостями при постоянном давлении и постоянном объеме существует следующая зависимость:

-для массовых теплоёмкостей:

, (1.37)

-для мольных теплоемкостей:

.(1.38)

Для приближенных расчетов и при невысоких температурах можно принимать следующие значения мольных теплоемкостей (табл. 1.3).

В технической термодинамике большое значение имеет отношение теплоемкостей при постоянном давлении и постоянном объеме, обозначаемое буквой k и называемое показателем адиабаты:

. (1.39)

Принимая теплоемкость постоянной, на основании данных табл. 1.3 можно получить для одноатомных газов k=1,67; длядвухатомных газов k=1,4; для трехатомных газовk=1,29.

Таблица.1.3.

Приближенные значения киломольных теплоемкостей газов при постоянном объеме и постоянном давлении (C = const)

Газы	Теплоемкость в кДж/(кмоль·К)
µСv	µCp
Одноатомные	12,56	20,93
Двухатомные	20,93	29,31
Трех - и многоатомные	29,31	37,68

Если в процессе участвуют М кг или V_нм³ газа, то подсчет количества тепла производится по формулам:

, (1.40)

и:

. (1.41)

Теплоемкость газовой смеси определяется на основании следующих формул:

массовая теплоемкость смеси:

(1.42)

oбъемная теплоемкость смеси:

(1.43)

мольная теплоемкость смеси:

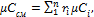(1.44)

где i – номер компонента смеси; n – число компонентов смеси.

В этих выражениях m_i, r_i – соответственно массовая и объемная доля i-го компонента газовой смеси; , , 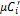– соответственно массовая, объемная и мольная теплоемкость i-го компонента; , , – соответственно массовая, объемная и мольная теплоемкость газовой смеси.

Дата добавления: 2017-01-14