Основные процессы изменения состояния идеальных газов

К основным термодинамическим процессам относят следующие четыре процесса:

изохорный – при постоянном объеме (V = const);

изобарный – при постоянном давлении (P = const);

изотермический – при постоянной температуре (T = const);

адиабатный – без теплообмена с внешней средой (dq = 0).

В реальных условиях указанные ограничения практически не выполняются. В связи с этим в технической термодинамике существует понятие политропного процесса как общего случая термодинамического процесса. Предполагается, что политропный процесс обратим и теплоемкость рабочего тела (идеального газа) C_n в ходе данного процесса не изменяется.

Уравнение политропного процесса имеет вид:

РVⁿ= const, (1.60)

где постоянная величина, называемая показателем политропы.

Политропных процессов существует бесчисленное множество, т. к.

Изохорный процесс

В диаграмме Рυ этот процесс изображается прямой 1-2, параллельной оси ординат. Уравнение прямой 1-2 (рис. 1.2), называется изохорной, V = const.

Зависимость между параметрами процесса:

(1.61)

Изменение внутренней энергии:

. (1.62)

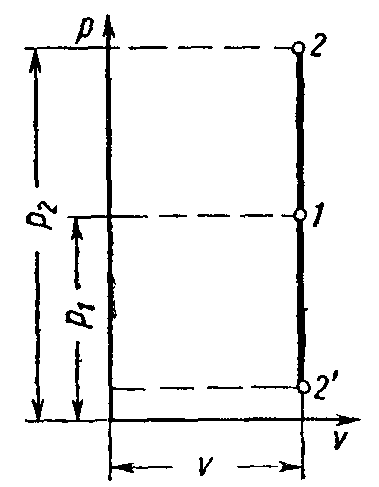
Рис. 1.2 Изображение изохорного процесса в координатных осях Pυ

Если в процессе участвует M, кг или V_н, м³ газа, то количество тепла или изменение внутренней энергии газа подсчитывается по формуле:

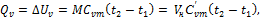(1.63)

где V_н – количество газа в м³ при нормальных условиях.

Если количество тепла необходимо подсчитать, пользуясь нелинейной зависимостью теплоемкости от температуры, то следует пользоваться формулой (1.40).

В изохорном процессе газ работы не совершает (L = 0).

Изобарный процесс

В диаграмме Pυ этот процесс изображается прямой 1-2, параллельной оси абцисс. Уравнение прямой 1-2 (рис. 1.3), называемой изобарой,

P = const.

Рис. 1.3 Изображение изобарного процесса в координатных осях Pυ

Зависимость между начальными и конечными параметрами процесса:

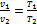. (1.64)

Работа 1 кг газа:

(1.65)

или:

(1.66)

Для M кг газа:

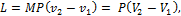(1.67)

или:

(1.68)

Если в процессе P=const участвует M, кг или V_н, м³ газа, то количество тепла подсчитывается по формуле:

(1.69)

где V_н – количество газа в м³ при нормальных условиях.

Если количество тепла необходимо подсчитать, пользуясь нелинейной зависимостью теплоемкости от температуры, то следует пользоваться формулой (1.41). Изменение внутренней энергии газа определяется по формуле (1.46):

,

или с учетом формулы (1.35):

Изотермический процесс

Кривая изотермического процесса, называемая изотермой, в диаграмме PV изображается равнобокой гиперболой (рис. 1.4).

Уравнение изотермы в координатах Pυ:Pυ = const.

Зависимость между начальными и конечными параметрами по формулам:

(1.70)

(1.71)

Рис. 1.4. Изображение изотермического процесса в координатных осях Pυ

Работа 1 кг идеального газа определяется из уравнений:

(1.72)

(1.73)

(1.74)

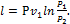(1.75)

Если в процессе участвуют М, кг газа, то полученные из формул (1.72)-(1.75) значения нужно увеличить в М раз. Можно так же для этого случая в формулах (1.74) и (1.75) заменить удельный объем υ полным объемом V. Получим:

, (1.76)

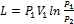. (1.77)

Так как в изотермическом процессе t = const, то для идеального газа:

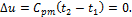
Количество тепла, сообщаемое газу или отнимаемого от него, равно:

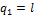, (1.78)

или для М, кг газа:

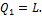(1.79)

Натуральный логарифм, входящий в формулы, может быть заменен десятичным по соотношению:

Адиабатный процесс

Уравнение адиабаты в системе координат Рυ (рис. 1.5) при постоянной теплоемкости (C_v = const) для идеального газа:

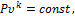
где 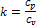- показатель адиабаты.

Зависимости между начальными параметрами процесса:

между Р и υ:

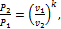(1.80)

между T и υ:

(1.81)

между Р и T:

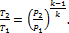(1.82)

Рис. 1.5 Изображение адиабатного процесса в координатных осях Pυ

Работа 1 кг газа определяется по следующим формулам:

(1.83)

(1.84)

(1.85)

(1.86)

Для определения работы М, кг газа нужно в формулах (1.83), (1.84) и (1.86) заменить удельный объем υ общим объемом V газа. Тогда получим:

(1.87)

(1.88)

(1.89)

Формула (1.85) для М, кг газа примет следующий вид:

(1.90)

Уравнение первого закона для адиабатного процесса имеет следующий вид:

следовательно,

,

или:

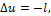(1.91)

т. е. изменение внутренней энергии газа и работа адиабатного процесса равны по величине и противоположны по знаку.

Изменение внутренней энергии идеального газа в адиабатном процессе может быть также выражено уравнением:

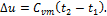(1.92)

Политропный процесс

Уравнение политропы в системе координат Рυ (рис. 1.6) при постоянной теплоемкости

где n – показатель политропы.

Показатель политропы n принимает для каждого процесса определенное числовое значение. Для основных процессов: изохорных n=±∞, изобарных n = 0, изотермных n = 1 и адиабатных n = k.

Теплоемкость политропного процесса определяем из формулы:

. (1.93)

Уравнение (1.93) позволяет определить теплоемкость политропного процесса для каждого значения n.

Если в уравнение (1.93) подставить значения n для частных случаев, то получаем теплоемкости рассмотренных процессов:

изохорного процесса n=±∞, C_n=C_υ;

изобарного процесса n=0, C_n=kC_υ=C_P;

изотермного процесса n=1, C_n=±∞;

адиабатного процесса n=k, C_n=0.

Рис. 1.6. Изображение политропного процесса в координатных осях Pυ

Характеристикой политропного процесса является величина:

(1.94)

которая может быть определена из выражения:

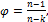(1.95)

где n – показатель политропы, а .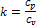

Зависимости между начальными и конечными параметрами процесса: между P и υ:

(1.96)

между T и υ:

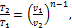(1.97)

между P и T:

(1.98)

Работа 1, кг газа в политропном процессе определяется по следующим формулам:

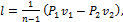(1.99)

(1.100)

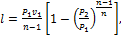(1.101)

(1.102)

Если количество тепла, участвующего в процессе, известно, то работа может быть также вычислена по формуле:

(1.103)

Для определения работы М, кг газа нужно в формулах (1.99)-(1.101) заменить удельный объем υ полным объемом газа V. Тогда:

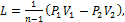(1.104)

(1.105)

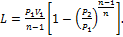(1.106)

Формулы (1.102) и (1.103) для М, кг имеют следующий вид:

(1.107)

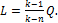(1.108)

Теплоемкость политропного процесса может быть определена из уравнения (1.94):

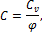
или, заменяя его значением из уравнения (1.95),

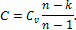
Количество тепла, сообщаемого газу или отнимаемого от него:

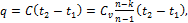(1.109)

(1.110)

Величина Q может быть так же определена из формулы (1.108), если известна работа политропного процесса:

(1.111)

Изменение внутренней энергии газа в политропном процессе находим либо по общей для всех процессов формуле:

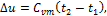
либо по формулам:

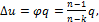
Изменение энтропии газа в политропном процессе определяется по формуле:

. (1.112)

Если известны значения двух параметров в начальном и конечном состоянии, то, пользуясь уравнениями (1.96)-(1.98), можно определить значение n из формул:

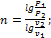(1.113)

(1.114)

(1.115)

Показатель политропы может быть также определен из уравнения (1.95). Решая его относительно n, получаем:

(1.116)

Дата добавления: 2017-01-14