Характеристики основных термодинамических процессов идеального газа

Второй закон термодинамики

Второй закон термодинамики определяет направление, в котором протекают процессы, устанавливает условия преобразования тепловой энергии в механическую, а также определяет максимальное значение работы, которая может быть произведена тепловым двигателем.

Второй закон термодинамики математически может быть выражен следующим образом:

(1.117)

Таблица. 1.5

Характеристика процесса	Название процесса
Изохорный	Изобарный	Изотермический
Показатель политропы	∞
Уравнение процесса	V=const; P/T=const	P=const; V/T=const	T=const; PV=const
Теплоемкость. кДж/(кг·К)	Cv	Сp=Cv+R	∞
Изменение внутренней энергии ∆u1-2=u2-u1 (кДж/кг)	Сv(Т2-Т1)	Сv(Т2-Т1)
Изменение энтальпии ∆h1-2=h2-h1 (кДж/кг)	Cp(Т2-Т1)	Сp(Т2-Т1)
Изменение энтропии ∆s1-2=s2-s1 (кДж/кг)	CvlnТ2/Т1	Сpln Т2/Т1
Количество теплоты q1-2 (кДж/кг)	Cv(Т2-Т1)	Сp(Т2-Т1)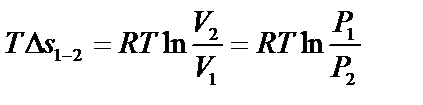
Работа изменения объема l1-2 (кДж/кг)		P(V2-V1)=R(T2-T1)
Работа техническая l’1-2 (кДж/кг)	-V(Р2-Р1)=v(P1- P2)= =R(T1-T2)		l’1-2= l1-2= q1-2= =

Продолжение табл. 1.3.

Характеристика процесса	Наименование процесса
Адиабатный	Политропный
Показатель политропы	k= Сp/Сv
Уравнение процесса	РV^k=const	РV^n=const
Теплоемкость. кДж/(кг·К)
Изменение внутренней энергии ∆u1-2=u2-u1 (кДж/кг)	Сv(Т2-Т1)	Сυ(Т2-Т1)
Изменение энтальпии ∆h1-2=h2-h1 (кДж/кг)	Сp(Т2-Т1)	Сp(Т2-Т1)
Изменение энтропии ∆s1-2=s2-s1 (кДж/кг)
Количество теплоты q1-2 (кДж/кг)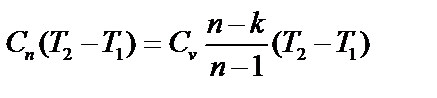
Работа изменения объема l1-2 (кДж/кг)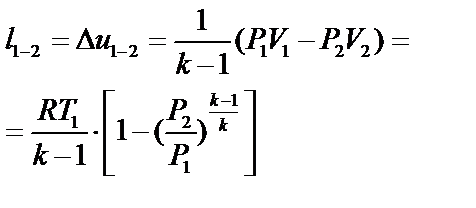
Работа техническая l’1-2 (кДж/кг)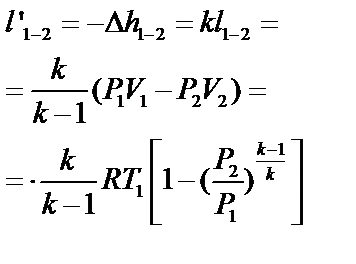

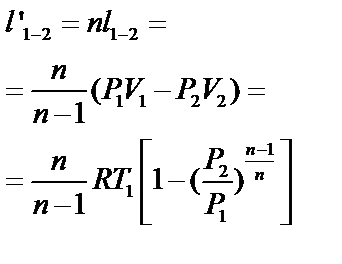
где dS – бесконечно малое приращение энтропии системы;dQ – бесконечно малое количество тепла, полученного системой от источника тепла;T – абсолютная температура источника тепла.

Знак неравенства соответствует необратимым процессам, а знак равенства – обратимым процессам. Следовательно, аналитическое выражение второго закона термодинамики для бесконечно малого обратимого процесса имеет вид:

(1.118)

а так как согласно первому закону термодинамики:

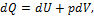
то уравнение (1.118) принимает следующий вид:

ЭНТРОПИЯ ИДЕАЛЬНОГО ГАЗА

Основным уравнением для определения изменения энтропии в обратном процессе является выражение:

(1.119)

Поскольку в технической термодинамике приходится иметь дело не с абсолютным значением энтропии, а с ее изменением, отсчет значений энтропии можно вести от любого состояния. Для газов принято считать значение энтропии равным нулю при нормальных условиях, т. е. при t = 0^oC и P = 760 мм.рт. ст.

Определение энтропии для любого состояния газа при постоянной теплоемкости, отсчитанной от нормального состояния, производят по следующим формулам:

(1.120)

(1.121)

(1.122)

Изменение энтропии между двумя произвольными состояниями газа 1 и 2 при постоянной теплоемкости определяют по следующим формулам:

(1.123)

(1.124)

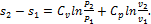(1.125)

Уравнения кривых различных термодинамических процессов в системе координат Ts имеют следующий вид (при постоянной теплоемкости):

уравнение изохоры:

(1.126)

уравнение изобары:

(1.127)

Взаимное расположение изохоры и изобары показано на рис. 1.7.

Рис. 1.7. Взаимное расположение изохоры и адиабаты в координатных

осях TS

уравнение изотермы:

T = const.

При этом изменение энтропии в изотермическом процессе равно:

(1.128)

Уравнение адиабаты:

s = const. (1.129)

Изображение изотермы и адиабаты в системе координат TS и Pυ дано соответственно на рис. 1.8 и 1.9.

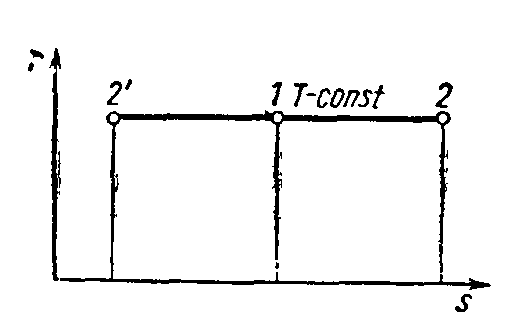
Рис. 1.8. Изображение изотермы в координатных осях TS

Рис. 1.9. Изображение адаибаты в координатных осях Pυ

Уравнение политропы:

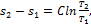(1.130)

где:

Широким распространением при решении термодинамических задач пользуется диаграмма TS. Адиабаты в этой диаграмме изображаются вертикалями, изотермы – горизонталями, изохоры и изобары идеального газа – логарифмическими кривыми.

Дата добавления: 2017-01-14