
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Гражданское право 2 страница
|
|
|
|
Берілген шифр бойынша нақты тапсырманы орындау барысында, талдап отырған мысалдан айырмашылығы, тәжірибедегі нұсқалар санының, жылдардағы басқаша кезеңдерінің, жылдардағы қайталау сандарының басқа екенін ескерген жөн. Ал бұл деректер есептеуге қатысады және оларға соңғы нәтиже тәуелді. Сондықтан жұмысты орындау барысында жеткілікті түрде ықыласты болу керек және өзіңнің нақтылы тапсырмаңның шартынан ауытқымаған жөн. Жұмысты (есепті) орындауды мына ретпен жүргізу ұсынылады.
1. Тапсырманың шифрымен белгіленген алғашқы деректерді өнімділіктің жинақы кестесіне көшіргеннен кейін, нұсқалар мен жылдар бойынша қосындылар есептелінеді.
2. «Нұсқалардың қосындысы» бағанының сандарын қосу арқылы жалпы қосынды Q табылады. Бұл қосынды біздің мысалымызда 136.7 тең
3. Жалпы қосындының Q дұрыстығы тексеру амалымен бақыланады. Ол үшін «Жылдардың қосындысының» жолдарының саны қосылады. Бұл жылдардың нәтижесі есептелінген Q шамасына тең болуы керек. Егер тексеру кезінде айырмашылықтар байқалса, бір жерден қате кеткендікті білдіреді сондықтан оны табу үшін жолдар мен бағандарды қайтадан қосып, іздейді.
4. Бүкіл тәжірибедегі көп жылдық орташа өнімділік M S Q шамасын l · n1 көбейтіндісіне бөлу арқылы табылады. Мұндағы l нұсқалар саны, n1 – тәжірибе жүргізілген жылдардың саны. Біздің мысалда ол, l · n1 = 4 · 3 =12. Олай болса, M S = Q: (l · n1) = 136,7: 12 = 11,4.
5. Әр нұсқа үшін жеке-жеке орташа өнімділік 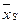 есептелінеді. Ол үшін нұсқалар бойынша қосындылары тәжірибе жүргізілген жылдардың санына бөлінеді. Біздің мысалымызда нұсқалар бойынша барлық қосындылар 3-ке бөлінеді.
есептелінеді. Ол үшін нұсқалар бойынша қосындылары тәжірибе жүргізілген жылдардың санына бөлінеді. Біздің мысалымызда нұсқалар бойынша барлық қосындылар 3-ке бөлінеді.
6. Нұсқалар бойынша есептелінген орташа өнімділіктердің дұрыстығы тексеру амалымен бақыланады. Ол үшін нұсқалар бойынша орташа өнімділіктің көрсеткіштері (4-баған) қосылады. Алынған қосынды сосын нұсқалар санына (бізде 4) бөлінеді. Бөліндінің нәтижесі бүкіл тәжірибедегі орташа өнімге M S сәйкес болуға тиіс. Нұсқалар бойынша шаманы 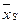 анықтаған (бұрынырақ) кезде дөңгелектеу нәтижесінде қателіктер болуы мүмкін. Сондықтан көптеген жағдайда баяндалған амалдың нәтижесінде M S шамасымен толық ұқсастық болмауы да мүмкін. Бірақ, мұндайда, айырмашылық 0,1 немесе 0,2-ден артуы немесе кемуі жағынан аспағаны жөн. Айырмашылық бұдан артық болса, 5-ші нұсқада көрсетілген қатені табу есептемелерін қайталау керек.
анықтаған (бұрынырақ) кезде дөңгелектеу нәтижесінде қателіктер болуы мүмкін. Сондықтан көптеген жағдайда баяндалған амалдың нәтижесінде M S шамасымен толық ұқсастық болмауы да мүмкін. Бірақ, мұндайда, айырмашылық 0,1 немесе 0,2-ден артуы немесе кемуі жағынан аспағаны жөн. Айырмашылық бұдан артық болса, 5-ші нұсқада көрсетілген қатені табу есептемелерін қайталау керек.
7. Көп жылдық орташа өнімділіктің 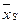 көрсеткіштерінің бақылау нұсқасынан айырмашылықтары ц/га және пайызда есептелінеді. Бақылаумен салыстырғанда өнімділік артса плюс белгісі, кемісе минус белгісі қойылады. Айырмашылықты пайызбен есептеуді еске саламыз (6-бағана). Ол үшін ц/га (5-ші бағана) берілген айырмашылықты 100-ге көбейтіледі және біздің мысалымыздағы, 11,2 ц/га тең, бақылаудың орташа өніміне бөлінеді.
көрсеткіштерінің бақылау нұсқасынан айырмашылықтары ц/га және пайызда есептелінеді. Бақылаумен салыстырғанда өнімділік артса плюс белгісі, кемісе минус белгісі қойылады. Айырмашылықты пайызбен есептеуді еске саламыз (6-бағана). Ол үшін ц/га (5-ші бағана) берілген айырмашылықты 100-ге көбейтіледі және біздің мысалымыздағы, 11,2 ц/га тең, бақылаудың орташа өніміне бөлінеді.
8. Қатенің шамасын m квадраттайды да, нәтижесін m 2 жолына жазады. Осы жолдан S m 2 есептелінеді.
9. Тәжірибе жүргізілген барлық жылдар үшін аумақтық қайталаманың n S жалпы саны анықталады. Жылдар бойынша қайталама саны бірдей болғанда олардың жылдағы n саны жылдардың санына n, көбейтіледі. Жылдар бойынша олардың саны әр түрлі болса n S саны n сандарын қосып анықталады. Осымен өнімділіктің жинақы кестесінің жұмысы аяқталады. Одан әрі жұмыс ауытқуларды есептеу кестелері бойынша жүргізіледі.
10. Аутқулардың есептеу кестесі дайындалады (17-кесте). Біздің мысалымыз бойынша кестеде барлығы төрт нұсқалардың жолдары бар. Ал, тапсырма бойынша жеті нұсқа қарастырылғанын ескерген жөн. Осыған байланысты ауытқуды есептеу кестесін дайындағанда жеті нұсқалық жол болуға тиіс.
11. Ауытқуларды есептеу кестесінде 1-бағанға нұсқалардың шартты белгілері, ал 2-бағанға, 4-кестенің негізінде, өнімділіктің жинақы деректері жазылады.
12. Нұсқалар бойынша өнімділіктердің жалпы орташадан M S ауытқу шамалары есептелінеді. Бұл айырмашылықтар 3-ші бағанда жазылады.
17-кесте - Ауытқуларға есептеулер
| Нұсқалар | Орташа өнімділік, 
| Ауытқу
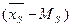
| Ауытқулар квадраттары

|
| А, бақылау | 11,2 | -0,2 | 0,04 |
| В | 11,7 | +0,3 | 0,09 |
| С | 13,4 | +2,0 | 4,00 |
| Д | 9,2 | -2,2 | 4,84 |
| M S = 11,4 | |||
| Қосынды | S 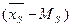 =+0,1 =+0,1
| 
|
Айырмашылықтардың дұрыстығы ауытқулардың алгебралық қосындылары арқылы есептелінеді. Айырмашылықтар дұрыс есептегенде 3-бағанның қосындыларының саны нөлге тең болуға тиіс немесе дөңгелектеудің қателіктері арқылы сәл ауытқуы мүмкін. Әдетте 3-бағанның қосындысы, не плюс, не минус болсын, 0,3 шамасынан аспайды. Егер 3-бағанның қосындысы 0,3-тен артық болса, онда мүмкін қателікті табу үшін, M S ауытқуды қайтадан есептейді.
13. Әр нұсқаның M S ауытқуын квадраттайды. Квадраттардың ауытқуларын 4-ші бағанға жазады. Содан кейін квадраттардың ауытқуларын 4-бағанның сандарын қосып табады. Біздің мысалымызда ондай қосынды 8,97-ке тең. Осымен ауытқуларды есептеу кестесі бойынша жұмыс аяқталады. Одан әрі есептеулер формуламен жүргізіледі.
14. Көп жылдық тәжірибе деректерінің жинақталған абсолютті және жинақтаған салыстырмалы қателерін есептейміз

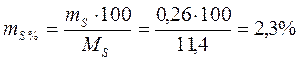
m S – тәжірибеніңжинақталған абсолютті қатесі, ц/га;
n 1 – тәжірибе жүргізілген жылдар саны;
Σ m 2 – тәжірибенің жылдағы абсолюттік қателерінің квадратталған қосындысы, ц/га (16-кестені қараңыз);
m S% - тәжірибенің жинақы абсолюттік қатесі;
M S – тәжірибедегі көп жылдық орташа өнімділік (16-кестені қараңыз).
15. Көп жылдық деректер дисперсиясының іс-жүзіндегі қатынасын табамыз.

 - көп жылдық деректер дисперсиясының іс-жүзіндегі ауытқуы;
- көп жылдық деректер дисперсиясының іс-жүзіндегі ауытқуы;
l – нұсқалар саны;
 - нұсқалардың орташа өнімділік айырмашылығының квадрат қосындылары, жалпы орташасымен M S (17-кестені қараңыз).
- нұсқалардың орташа өнімділік айырмашылығының квадрат қосындылары, жалпы орташасымен M S (17-кестені қараңыз).
Енді  -ті Фишер критерийінің кестелік мәнімен төмендегі еркіндік дәрежелерімен салыстырамыз:
-ті Фишер критерийінің кестелік мәнімен төмендегі еркіндік дәрежелерімен салыстырамыз:
ν 1= l –1 = 4 – 1 = 3;
ν 2 = (nS – 1) (l –1) = (15-1) (4-1) = 42;
ν1, ν2 – еркіндік дәреже көрсеткіштері;
nS – тәжірибе жылдарындағы аумақтық қайталамалардың қосынды саны (16-кестені қараңыз).
Фишер критерийінің стандартты (кестесі) мәні, тәжірибе ісі әдістемелік көптеген оқулықтардың қосымшаларынан іздестіріледі. Танаптық тәжірибелер үшін мән деңгейі 5%-ды кесте алынады. Б.Д.Доспеховтың 1985 жылғы оқулығында мұндай кесте 318 бетте орналасқан. Оқу құралында мұндай кесте бар (1-қосымшаны қараңыз). Кестеден ν1 бағанына және ν2 жолына сәйкес көрсеткіштерді іздеп табамыз. Осы баған мен жолдың тоғысқан жерінде Фишер критерийінің FT кестелік мәніне сәйкес көрсетіледі (болады). Стандартты мәннің кестесі әр түрлі деңгейлі толықтықпен жасалынатындықтан, ν1 мен ν2 -нің нақты көрсеткіштері жол мен бағандардың аралағында болуы мүмкін. Біздің мысалымыз үшін кестеде ν1 =3 сәйкес баған барда, ν2 =42 сәйкес жол жоқ, яғни 40 пен 50 жолдарының арасында болып шығады. Мұндайда, жылдағы дисперсиялық талдаулардағыдай аралық көрсеткішті жуықтап табу күрделі емес. Бағандағы ν2 =40 –тан ν2 =50 –ге дейін FT мәні небары 0,05-ке кемиді, яғни 2,84-тен 2,79-ға дейін. Осыған орай ν1 =3 және ν2 =42 болғанда FT мәні 2,83-ке тең деуге болады.
Кестеден көргеніміздей, ν2 мәні артқан сайын Фишер критерийінің өзгеруі шамалы. Сондықтан осы жерде FT -ңаралық мәнін іздестіру қиынға түспейді.
Тәжірибенің көп жылдық дерегін Фишер критерийі бойынша бағалау былай жүргізіледі. Егер F'Ф > FT болса, онда тәжірибе нұсқалары арасындағы орташа өнімділіктерде айтарлықтай айырмашылықтар мүмкін деуге болады. Ал, егер F'Ф < FT болса, онда нұсқалар арасында айтарлықтай айырмашылықтар жоқ және одан әрі жұмысты тоқтату керектігін білдіреді. Оқулық сабақтарда танаптық тәжірибелердің көп жылдық деректерін статистикалық өңдеу әдістерін толық меңгеру мақсатында, Фишер критерийінің іс-жүзіндегі кез келген мәніне қарамай есептеу жұмыстары соңына дейін жүргізіледі.
Біздің мысалымыздағы есептеуде табылған F'Ф = 42,7-ң кестеден алынған FT = 2,83 стандартты мәнінен бірнеше есе артық екенін көріп отырмыз. Осыдан, тәжірибенің нұсқалары арасында айтарлықтай айырмашылықтар бар, сондықтан оларды арнаулы критерийідің – ең төмен (аз) елеулі айырмашылықтың (ЕТЕА) – көмегімен анықтайды.
16. Айырмашылықтардың m ds жинақы қатесін және ең төмен елеулі айырмашылықты (ЕТЕА) анықтаймыз. Мұндағы 05 индексі танаптық тәжірибе жағдайында ЕТЕА 5% мәнділік деңгейінде анықталады, ықтималдық деңгейі 0,95 немесе 0,95% сәйкес келетіндігін білдіреді.
m ds = 1,41 · m s = 1,41 · 0,26 = 0,37 ц/га
1,41 – тұрақты шама және  тең.
тең.
ЕТЕА'05 = t 05 · m ds
Бұл формула бойынша есептеу жүргізу үшін, Стьюдент критерийінің t 05 5% мәнділік деңгейіндегі мәнін, ол 0,05 санымен белгіленеді, табу керек. Жоғарыда аталынған Б.А.Доспеховтың оқулығында Стьюдент критерийінің кестелік стандартты мәні 317 бетте болса, практикумның 1 – қосымшасында. Қажетті жолды табу үшін еркіндік деңгейінің саны ν2 көрсеткіші бойынша алынады, ал ол бізде есептелінген. Ол 30 және 50 сандарымен белгіленген жолдардың арасында орналасқан. Берілген деңгейдегі бағанда 0,05 мәнділік деңгейдегі 30 және 50 сандарының еркіндік деңгейіне t 05 шамасына 2,04 және 2,01 сәйкес келеді. Осы сандарды ескеріп еркіндік деңгейінің ν2 =42 санында t 05 аралық мәні 2,02 тең деуге болады.
Осы сандарды жоғарыдағы формулаға қойып, табамыз:
ЕТЕА'05 = 2,02 · 0,37 = 0,75 ц/га
Осымен есептеулер аяқталады.
17. Тәжірибенің көп жылдық деректерін ең төмен елеулі айырмашылықтың көрсеткіштері бойынша бағалау жылдағы деректерді дисперсиялық талдау негіздерімен бағалауға ұқсас. Өнімділік бойынша көп жылдық орташа айырмашылық тәжірибенің кез келген нұсқаларын салыстырумен, бағалануы мүмкін. Бірақ өнімділік деректерін бақылаумен салыстырудың мәні ерекше. ЕТЕА'05 бойынша бағалау бақылаумен қаншалықты айырмашылық елеулі емес деген сұраққа жауап береді, яғни тәжірибе қатесі шегінде деген. Жылдағы дисперсиялық талдаудағы сияқты, қосымшаның ғана елеулігі бағаланбайды, сонымен бірге өнімділіктің төмендеуі де бағаланады. Кез келген айырмашылық, ол қосымша өнім немесе бақылаумен салыстырғанда төмендеу болсын, егер ол ЕТЕА'05 -тің шамасынан төмен болса, елеулі емес және тек кездейсоқтың есебінен пайда болған деп саналады. Елеулі деп ЕТЕА'05 -тен не артық не оған тең айырмашылығы саналады.
18. ЕТЕА'05 -ң көрсеткішіне және зерттелген нұсқалардың бақылаумен (16-кестенің 5-бағанына қараңыз) салыстырғандағы көп жылдық орташа өнімділігінің есептелінген айырмашылығына сүйеніп жазбаша қорытынды жасалынады. Біздің мысалымыз бойынша жазбаша қорытындының үлгісін келтірейік.
Тапсырмада, үлгідегідей бақылаумен 3 нұсқа емес 6 нұсқа салыстырылатынын ескертеміз. Сондықтан қорытындыда 6 нұсқаның да елеулілігі бағалануға тиіс.
1. «В» нұсқасы бойынша 0,5 ц/га өнімділік елеулі емес деп саналады, себебі ол ЕТЕА'05 шамасынан кем.
2. «С» нұсқасы бойынша өнімділіктің 2,2 ц/га артуы және «Д» нұсқасы бойынша 2,0 ц/га төмендеуі елеулі деп саналады, себебі олар ЕТЕА'05- тің шамасынан артық.
Осымен жұмыс аяқталады және оқытушыға тексеруге тапсырылады.
VII. ТУРА СЫЗЫҚТЫ КОРРЕЛЯЦИЯ
1. Негізгі түсініктер
Корреляция латын тілінен аударғанда байланыс, тәуелділік, арақатыс, ілесетін дегенді білдіреді. Өзара қатысты екі белгінің немесе құбылыстың, егер бірі ұлғайғанда сонымен байланысты белгінің екіншісі тұрақты салыстырмалы түрде біркелкі ұлғайса, немесе, керісінше тұрақты түрде біркелкі кемісе мұны тұрақты сызықтық корреляция деп түсіну керек. Біріншісін түзу, екіншісін кері корреляция деп атайды.
Түзу коррелятивтік тәуелділіктің мысалы ретінде өнімділіктің жазғы жауын-шашынға байланыстылығын айтуға болады. Бәрімізге де белгілі, жаңбырлы жаздан кейін әдетте өнімнің жоғары болатыны. Басқа бір белгілер жұбын – 1 м2-гі арамшөп саны мен өнімділікті алайық. Бұл жолы анық кері корреляция байқалатын болады: бір өлшем жерде арамшөп саны неғұрлым көп болса, соғұрлым өнімділік төмен.
Мына байланыстар коррелятивтікті зерделеудің мысалы бола алады: топырақтың ылғалдылығы және өнім, пісу мерзімі және өнім сапасы, топырақ қуыстылығы (кеуектілік) және оның ылғалдылығы, топырақтың өңдеу тереңдігі және қоректік режімі, қар жинастыру (тоқтату) және өнімділік, тамыр жүйесінің даму қуаты және құрғақшылыққа төзімділік және т.т.
Тура сызықты корреляцияны тура немесе кері пропарционалды тәуелділіктің нағыз өзі деп қарастыруға болмайды. Агрономиялық зерттеулердің зерзаттары (объектілері) - өсімдіктер мен олардың тіршілік жағдайлары, өлшеуге және есепке алуға қиын соғатын, немесе алдын ала болжауға болмайтын, көптеген кездейсоқ құбылыстарға душар болады. Мысалы, жазғы жауын-шашын жиынтығын және өнімділікті алайық. Жазғы жауын-шашын жиынтығынан басқа, олардың жаз бойы түсу мерзімінің, топырақтағы су қорының, сондай-ақ ауа температурасының маңызы да зор. Әр жылдардағы атқарылатын танаптық жұмыстар да абсолютті бірдей болуы мүмкін емес.
Осыған байланысты зерттеушінің алдынан белгілер мен құбылыстардың арасында байланыс бар ма деген сұрақтан басқа, бұл байланыстарды, әр түрлі кездейсоқ факторлардың жанама әсерлері болғанда, қалай өлшеу керек деген сұрақ та туындайды.
Тура сызықтық коррелятивтік байланыс деңгейінің өлшегіші болып корреляция еселігі саналады. Тура корреляцияда еселікке (коэффициентте) плюс, керісінде – минус белгісі болады.
Корреляция еселігі нөлден бірге дейін өзгереді. Корреляция еселігінің шамасы бойынша коррелятивтік байланыстың деңгейін анықтайды: 0-ден 0,33-ке дейін - әлсіз (байланыс жоқтың қасы); 0,33-тен 0,66-ға дейін – орташа; 0,66-дан 1,00-ге дейін – күшті, 1,00- толық корреляция делінеді.
Төменде жылдық жауын-шашын жиынтығы, мм Х (факторлық белгі, тәуелсіз айнымалы шама) пен астық дақылдарының өнімдерінің ц/га У (нәтижелік белгі, тәуелді айнымалы шама) арасындағы коррелятивтік байланысты өлшеп, корреляция еселігін есептеу және оның дәлдігін нақты мысал негізінде бағалау жұмысының орындау барысы баяндалған.
Корреляция еселігін есептеудің бірнеше тәсілі бар. Тәсілді таңдау негізінен таңдау санына, яғни талдайтын белгілер жұбының санына байланысты. Агрономиялық зерттеулерде тура сызықтық тәуелділік әдетте шамалы таңдаулармен жеткілікті тәуелділікпен табыла береді, кейде небары 6-7 жұппен. Осы тақырыпта біз шамалы таңдаулармен және қарапайым есептегіш құралдарды (калькулятор) қолданып тиімді жұмыс істеуге қолайлы тәсілді таңдадық.
Жоғарыдағы мысалды басшылыққа ала отырып, студент оқытушы берген жеке тапсырманы орындай алады.
1. Әр студент алғашқы есептеулердің кестесін дайындайды (18- кесте). Жеке тапсырмалардың көлемін ескеріп, кестеде 28 жұмыс жолы қарастырылады. Жұмыс орындау қолайлы болу үшін кестені дәптердің екі бетіне сызу керек. Кестенің 2-ші және 3-ші бағандарын Х және У әріптерімен белгілеу керек.
Әңгіме мынада, жеке тапсырмаларда нақты емес, бір және екі таңбалы сандар түріндегі абстракты көрсеткіштер беріледі. Абстаркты көрсеткіштерді қолданудың себебі, тапсырманың бір кестесінен әр түрлі сипаттағы жауаптар алынатындығынан. Осыған байланысты тура және кері корреляция шынға ұқсас болатындай етіп айқын көрсеткіштерді таңдап алу мүмкін емес. Бұл агрономиялық зерттеулердің қисынына (логикасына) қайшы болар еді. Бірақ сандар мен формулалар арқылы өсімдік пен жерді көре білсек, нәтиже мүмкін нұсқалардың өзара мүмкін қарым-қатынастарын көрсете алар еді. Айтайық, нәтижесінде тура корреляция анықталса, онда х белгісі ретінде, мысалы, өсімдік сабағының ұзындығын, ал у белгісі ретінде – бір өсімдіктегі жапырақ санын көрсетуге болады. Жұмыстың нәтижесінде кері корреляция анықталынған болса, х және у белгілері ретінде сәйкес 1 м2-гі арамшөп санының мәдени өсімдіктердің топырақ үстілік массасының грамдағы орташа салмағына байланысын көрсетуге болады. Жалпы, корреляциялық талдаудың техникасын кез келген санда, нақты, сондай-ақ таңдалынып алынған жасанды сандарда да игеруге болады.
2. 18-кестенің х және у бағандарына бастапқы есептеулері оқытушыдан алынған жеке тапсырмаға сәйкес толтырылады. Барлық тапсырмалар тапсырманың кестесіне шоғырланған (19-кесте).
Жеке тапсырма алудың ретін мысалмен түсіндірейік. Айтайық: х-7б деген тапсырма берілді. Бұл студент бастапқы есептеулер кестесінің х бағанына тапсырма кестесінің «б» бағанының 7-ші жолының 21-ші санынан бастап және одан төмен: 23, 25 ж т.т. қояды (көшіреді). 18-ші есептеу кестесінде мысал ретінде тапсырма кестесімен байланысы жоқ басқа сандар алынған. Сандар жиынтығы тапсырма кестесінің соңында, есептеудің бастапқы жолы белгіленген нөмірмен аяқталуға тиіс. Мысалдағы 7 б тапсырмасында сандар жиынтығы төменде 7 жолмен аяқталады, яғни берілген тапсырмада соңғы сан 95 болады. Осыған ұқсас у белгілері бойынша тапсырманың сандары қойылады. Айтайық, мысал үшін, 2 ж тапсырмасы жоғары жағында «ж» бағанының 2-ші жолында 16 санымен басталады және сол екінші нөмірмен белгіленген бағанның төменгі жағында 74 санымен аяқталады. Сонда, тапсырманың бірінші және соңғы сандарын қоса, х көрсеткіші бойынша, сондай-ақ у көрсеткіші бойынша әр қайсысы 28 саннан алуға тиіс. Тік бойындағы сандардың реті тапсырма кестесіндегідей болуға тиіс: сандардың қандай да бір орнын ауыстыруға болмайды.
18-кесте – Корреляция еселігін анықтауға арналған бастапқы есептеулер
| Жұп-тар нөмірі | Жауын-шашынның жылдық жинақталған қоры, мм* (х) | Астық дақылдары-ның өнімділігі, ц/га*(у) | ах=х- 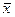 
| ах2 | ау=у- 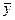
| ау2 | ахау |
| 2,2 | -112 | -5,4 | 29,16 | +605 | |||
| 10,0 | -83 | +2,4 | 5,76 | -199 | |||
| 6,8 | -18 | -қ,8 | қ,64 | +14 | |||
| 11,2 | +44 | +3,6 | 12,96 | +158 | |||
| 10,3 | +76 | +2,9 | 7,29 | +205 | |||
| 7,6 | +63 | 0,0 | 0,00 | ||||
| 6,5 | -13 | -1,1 | 1,21 | +14 | |||
| 6,3 | -42 | -1,3 | 1,69 | +55 | |||
| 3,3 | -24 | -4,3 | 18,49 | +103 | |||
| 11,8 | +105 | +4,2 | 17,64 | +441 | |||
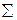 х=3126 х=3126
| 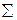 у=76,0 у=76,0
| 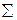 ах=-4 ах=-4
| 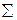 ах2=44972 ах2=44972
| 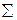 ах=0,0 ах=0,0
| 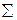 ах2=94,84 ах2=94,84
| 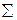 ахау=+1396 ахау=+1396
|
|
|
|
|
|
Дата добавления: 2017-02-01; Просмотров: 72; Нарушение авторских прав?; Мы поможем в написании вашей работы!