Гражданское право 3 страница

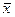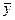=313 =7.6

*Берілген шифр бойынша есептеулер жүргізілгенде 2-ші және 3-ші бағандағы тәуелсіз айнымалы (х) және тәуелді айнымалымен (у) деп атау дұрыс болады.

3. Жұмыс барысы

1. 18-кестенің пішіні және үлгісі бойынша есептеу негізі.

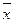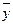Есептеу реті мынадай: х және у бағандары бойынша қосындысы және пен -тің орташа шамалары есептелінеді. Кейде орташалар бірнеше ондық таңбалармен шығады. Мұндайда үш орынды цифрға дейін дөңгелету жүргізеді. Бұл не? Егер орташа 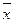пен 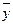-тің шамасы 10-нан кем болса, онда дөңгелетуді жүздікке дейін жүргізеді. Ал, егер олардың шамасы 10-нан 100-ге дейін ауытқыса, онда дөңгелетуді ондыққа дейін қолданады. Егер орташа көрсеткіштері 100 және одан жоғары болса, дөңгелетуді бүтін санға дейін жүргізеді. Біздің тапсырмаларымызда шама деңгейі дөңгелетуді ондыққа дейін жүргізуді тілейді.

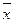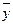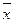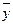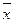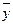Х-тің және У-тің әр шамасының пен орташа шамасынан ауытқуы есептелінеді. Жазуларды а_х және а_у сәйкес бағандарда жүргізеді. а_х-тің әр шамасы (Х- ) формуласының қысқартылған түрі. Сондай-ақ а_у та (У- ) формуласынікі. а_х пен а_у сандарының плюс таңбасы Х және У-тің шамалары, пен -тің орташа шамаларынан артық болғанда қойылады. Егер олар орташа шамалардан кем болса, онда минус қойылады.

4-ші және 6-шы бағандар бойынша ∑ а_х пен ∑ а_у-тің алгебралық қосындысы есептелінеді. Осы қосындылар бойынша бұрынғы есептеулердің дәлдігі тексеріледі. Егер 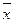және 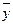-тің шамалары (орташа нәтижелері) берілген дәлділік шегіндегідей шықса, онда 4-ші және 6-шы бағандардың алгебралық қосындылары, алдыңғы есептеулер дұрыс болған жағдайда, нөлге тең болуға тиіс. Айтайық, біздің мысалымызда (18-кестені қараңыз) у-тің орташа көрсеткіші дөңгелетуді қажет етпеді. Демек, Еа_у жиынтығы нөлге тең болуға тиіс, міне 6-шы бағанның қосындысы солай болып шықты.

Осыдан, У белгісімен байланысты барлық есептеулер әзірше дұрыс және У одан бұрынғы есептеулерін тексерудің қажеті жоқ деген қорытынды жасаймыз.

Егер 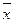және 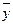шамаларын дөңгелетуде қателер болса, тексеру қиынға соғады.

19-кесте – «Тура сызықты корреляция» тақырыбына тапсырма

Санау жолы	Х белгici	У белгici
а	б	в	г	д	е	ж	з	и	к

Біріншіден, Σ а_х пен Σ а_у жиынтықтарының ықтималды максимумының мүмкін шамасы анықталады. Ол үшін 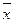және 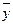-тің сандарының соңғы разрядының санына зерделінетін белгілер жұбының саны көбейтіледі және екіге бөлінеді. Соңғы разрядтың саны дегенді қалай түсінеміз? Екі ондық таңбалы сандарда соңғы разрядтың саны 0,01 тең, бір ондық таңбалы сандарда ол 0,1. Бүтін сандар, яғни ондық таңбасыз сандарда соңғы разряд саны болады. Біздің талдау мысалымызда (18-кестені қараңыз) 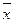саны бойынша соңғы разрядтың саны 1 болады, ал 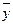саны бойынша соңғы разрядтың саны 0,1 тең. У белгісі бойынша дөңгелектеу кестесі болмағандықтан, бұл мысалда тексеруді тек ∑а_х жиынтығы үшін жүргіземіз:

1· n: 2 =1 · 10: 2 = 5,

мұнда n – талданатын белгілердің жұп саны. Осы мысалда талдауға 10 жұп қатысады. Ал, біздің тапсырмамызда әр студентке 28 жұп белгі берілгенін ұмытпаған жөн.

Жоғарыда жүргізілген есептеулер негізінде, Σ а_х жиынтығының рұқсат етілген мүмкін максимумы плюс таңбасында, сондай-ақ минус 5 шамасынан аспайды деген қорытынды жасалынады. Біздің мысалымызда Σ а_х = - 4. Бұл шама рұқсат етілген максимумнан аспайды деп қорытынды жасаймыз.

Екіншіден, формула бойынша тексеру жүргізіледі:

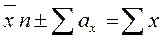
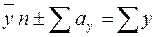
Бұл формулалардағы плюсті немесе минусты таңдау, 4-ші және 6-шы бағандар жиынтығына сәйкес таңбаларға тәуелді болады.

Талдап отырған мысалымызда (18-кестені қараңыз) тексеру былай жүргізіледі:

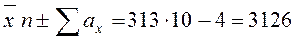
Соңғы сан åх шамасына сәйкес осының негізінде, åх қосындысы, орташа нәтиже 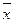және барлық ауытқулар а_х дұрыс есептелген деген қорытынды жасалады. Осыған ұқсас У шамасымен байланысты есептеулердің дұрыстығын тексеру есептемелерін жүргізуге болады. Бірақ, алдында айтқанымыздай, У-тің орташасын дөңгелетуде қателіктер болған жоқ. Дәл осы жағдайда åа_у 0-ге тең болуы, У белгісімен байланысты алдыңғы есептеулерінің сенімді дәлелі бола алады. Егер åа_х пен åа_у-тің қосынды нәтижелері алдыңғы есептеулердің дұрыстығын дәлелдей алмаса онда қосулардың, орташа нәтиженің және ауытқулардың дұрыстығын тексеру есептері қашан қателер табылғанша жүргізіледі.

а _х және а _у сандарын квадраттау жүргізіледі де, нәтижесі сәйкес 5-ші және 7-шы бағандарға сәйкес жазылады. Мұндайда дөңгелектеу 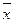және 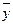орташа мәндерін есептегендей (жоғарыдан қараңыз) шешіледі, яғни 3 мәнді цифрға дейін. Сонымен бірге бірдей бағанда, айтайық, бесінші бағанда, ах² үлкен де (жүздікте және мыңдықта) және кіші де (оннан аз және бірден де) болуы мүмкін. Мұндайда күткен үлкен сандарға сүйенген дұрыс. Айтайық, мысалы, егер квадраттағаннан кейін 100-ден жоғары сандар көбірек болса, онда барлық сандарды (үлкенін де, кішісін де) бүтінге дейін дөңгелектейді.

Квадраттағаннан кейін бесінші және жетінші бағандардың åах² және åау² қосындылары есептелінеді. Кестенің соңғы сегізінші бағаны 4-ші бағанның сандарын алтыншы бағанның сандарына көбейтіп шығарылады (жазылады). Сегізінші бағанның сандарын дөңгелектеуде бесінші және жетінші бағандардікіне ұқсас жүргізіледі (жоғарыдан қараңыз). Осыдан кейін сегізінші бағанның плюс және минус сандарын өзара қосады және жалпы алгебралық қосындысы åа_х åа_у табылады.

2. Корреляция еселігін есептеу және корреляциялық байланыстың деңгейін бағалау

Корреляция еселігі r формуламен жүздікке дейін дәлдікпен есептеледі:

Бұл формуламен есептеу кезінде бөлшек астындағы көбейтіндінің нәтижесімен квадрат түбірін шығару қиындық туғызуы мүмкін. Себебі, көбейтіндінің нәтижесі 5 таңбалы және одан да көп сан болуы мүмкін. Квадрат түбірін шығаруды жеңілдетуге болады, егер алдымен әр көбейткіштің түбірін жеке-жеке шығарып, сосын шыққан сандарды бірімен бірін көбейте салу арқылы.

Бастапқы есептеулер кестенің (18-кестені қараңыз) сандарын жоғарыдағы формулаға орны-орнына қоя отырып, радикалдағы түбірдің бір саны бес таңбалы екенін байқаймыз. Осыған орай көбейткіштердің түбірін табуды жеке-жеке жүргіземіз. Алғашқы жазбамыз мынандай болады:

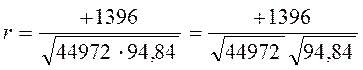
Енді, жоғарыда басталынған корреляция еселігін есептеуді аяқтауға болады:

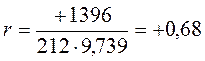
Корреляция еселігінің алдындағы плюс және минус таңбалары коррелятивтік байланыстың бағытын анықтайтынын тағы да ескертеміз. Егер корреляция еселігі плюс таңбалы болса, онда оны тура байланыс, ал минус таңбалы болса, кері байланыс деп есептейді. Осы мысалдарымыздың нәтижесіне сүйеніп, коррелятивтік байланыс деңгейінің қабылдаған градациясының негізінде («негізгі түсініктер» деген тараудан қараңыз) біз корреляция еселігіне r=+0,68 сәйкес Х және У белгілерінің арасында өте күшті коррелятивті тура байланыс бар деген қорытындыға келеміз. Сонымен бірге, корреляция еселігі х белгісінің у белгісінің өзгеруінде қаншалықты қатысы бар екені жөнінде нақты сандық қатысын ашып көрсете алмайтынын ескерген жөн. Зерттелініп отырған белгілердің біреуінің екінші біреуінің өзгеруіне қатысу үлесін анықтау үшін, корреляция еселігінің квадратына тең, детерминация d_YX еселігі есептелінеді.

Өзіміздің мысалымызды жалғастыра отырып, анықтаймыз:

d_YX = r² = 0,68² = 0,46

Осыдан, Х белгісінің У белгісіне тигізетін әсер үлесі, барлық әсерлердің 0,46-сын немесе 46 % қамтиды деп қорытынды жасауға болады.

3. Корреляция еселігінің дәлдігін z көрсеткіші арқылы бағалау

Корреляция еселігі басқа да көптеген статистикалық көрсеткіштер сияқты, жеткілікті және жеткілікті емес дәлдікке ие болуы мүмкін. Корреляция еселігінің дәлдігін бағалайтын бірнеше тәсіл белгілі. Бірақ ең әмбебап, әсіресе зерттеуде белгілер жұбы шамалы болғанда және тиімдірегі болып z (зет) көрсеткіші (5-қосымша) арқылы бағалау саналады.

Осы практикумның іс саналық (практикалық) бағыттылығын ескеріп, біз z көрсеткішін санауды қоя тұрамыз. Қажет болса онымен Б. А. Доспеховтың 1973 жылы басылып шығарылған оқулығынан (180-181 бетінде) және Г.Ф. Лакиннің 1980 жылы басылып шыққан оқу құралынынан (160-161 бет) оқып білуге болады. Бұл әдебиеттер жөнінде толық анықтама осы оқу құралының соңында келтірілген. Ал, қазір біз z көрсеткіші бойынша есептелінген корреляция еселігінің ауыспалы мәнін ғана кестеден көшіріп аламыз. Кестеден, көптеген агрономиялық зерттеулер үшін жеткілікті, 5 % мәнділік деңгейін ғана келтіреміз (20-кесте). 5% мәнділік деңгейі 100 мүмкіндіктің тек бесеуі ғана осы кестенің көрсеткіштері бойынша қате болатынын білдіретінін тағы да ескертеміз. Корреляция еселігінің ауыспалы мәнінің кестесі толығырақ Б.А. Доспеховтың (313-бет) және Г.Ф. Лакиннің (285-бет) кітаптарында келтірілген.

Корреляция еселігінің дәл шамасының ауыспалы мәнін кесте бойынша бағалау мына ретпен жүргізіледі. N бағанынан зерттелуге тиіс белгілер жұбының саны ізделініп табылады. Біз талдап отырған мысалда n = 10 тең. 5-ші бағанда осы санға қарсы 0,632 санын көреміз. Міне, сол корреляция еселігінің ауыспалы мәні болып табылады. Келтіріліп отырған 20-кесте пішіні бойынша жеңілдетілген. Оқулық әдебиетте корреляция еселігінің ауыспалы мәнін іздестіру негізіне таңдау (n) мөлшері емес, еркін дәреже (n-2) саны алынады.

Егер есептелініп алынған корреляция еселігі ауыспалы мәнінен артық болса, онда оның дәлділігі жеткілікті саналады. Ал, егер есептелініп алынған корреляция еселігі ауыспалы мәнінен кем болса, онда дәлділігі жеткілікті емес деп саналады. Осы жағдайда, ауыспалы мәні шамасынан кем болса, корреляция еселігі анық емес (сенімсіз делінеді).

Осы мысалда есептелініп алынған корреляция еселігінің шамасына, r = +0,68-ге көңіл бөлейік. Бұл шама 20-кесте бойынша анықталған 0,632 ауыспалы мәнінен артық.

Осыдан, есептелінген корреляция еселігі жеткілікті дәлдікте деп тұжырым жасаймыз.

Табылған корреляция еселігінің сенімділігін оның стандартты қатесін және елеулілік критерийін есептеумен де бағалауға болады (5). Стандартты қатесін мына формуламен анықтайды:

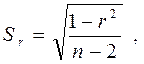
мұнда S_r – корреляция еселігінің стандартты қатесі;

r - корреляция еселігі;

n – таңдау саны, яғни корреляция еселігі есептелінген нұсқалардың жұп саны.

Формуладан байқағанымыздай бірге жақын корреляция еселігі, 0-ге жақын корреляция еселігінен дәлірек келеді. Таңдау саны артқан сайын стандартты ауытқу S_r кеми береді де, ал корреляция еселігінің r анықтау дәлділігі арта түседі.

Корреляция еселігінің елеулілік критерийі мына формуламен есептелінеді.

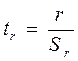
Егер t_{r факт.} ≥ t_теор. болса, онда корреляциялық байланыс елеулі, ал егер t_{r факт.} ≤ t_теор. болса – елеулі емес. Корреляция еселігінің критерийінің теориялық мәнін Стьюдент кестесі бойынша (4-қосымша), маңыздылық деңгейін 5 % деп алып, табады. Еркіндік дәреже санын n – деп алынады.

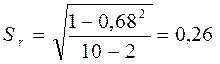
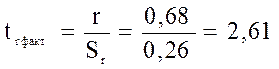
t_теор. – еркін дәрежесенің саны n-2 = 10-2=8 болғанда 2,31 тең.

Стьюдент критерийінің шын (факт.) және кестелік мәндерін салыстырамыз:

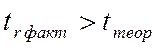= 2,61> 2,31

Қорытынды жасаймыз: 10 жұп талдаудан зерттелген корреляция еселігі елеулі деп. Әдетте корреляция еселігі стандартты қатемен r ± 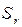жазылады. Біздің мысалымызда 0,68±0,26.

Детерминация (d_YX) еселігінің анықтығын Фишер критерийі бойынша мына формуламен есептейміз:

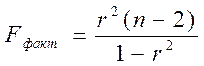
Біздің мысалымызда F_факт. тең болады

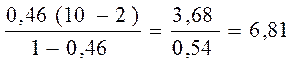
Еркіндік дәреже саны ν₁ = 2 – 1= 1, ν₂ = 10 – 2 = 8. F_кест. 1-қосымшада 5,32 тең. Осыдан F_факт. > F_кест. себебі 6,81 > 5,32.

Қорытынды жасаймыз: дәнді дақылдардың өнімділігі мен жылдық жауын шашын жиынтығы арасында тура сызықты тәуелділік бар деп.

Жүргізілген есептеулердің көмегімен корреляция еселігінің (Стьюдент критерийі) және детерминация еселігінің (Фишер критерийі) елеулілігі дәлелденеді.

Коррелция еселігін дәл анықтау негізінде таңдаудың қажетті ең аз саны анықталады, яғни зерттелетін белгілердің қажетті жұп саны белгіленеді. Егер корреляция еселігі қажетті дәлділікке жетпесе (20-кесте бойынша ең аз ауыспалы мәні), таңдаудың санын неше жұпқа жеткізгенде, корреляция еселігі күдік туғызбайтынын білуіміз керек. Мынадай жағдайлар да кездесуі мүмкін: корреляция еселігі жеткілікті дәлдікте болуы үшін белгілер жұбы тым көп алынады, ал іс жүзінде аз жұп санымен де дәлдікті дәлелдеуге болар еді. Зерттеу жұмысында мұның да өзіндік маңызы бар, себебі зерттелетін белгілердің артық жұп саны – бұл тым көп артық жұмыс: өлшеуге, санауға, талдауға және ж.т.т.

Талдаудың қажетті ең аз саны да корреляция еселігінің ауыспалы мәндерінің кестесі (20-кестені қараңыз) бойынша анықталады. Ол үшін ауыспалы мәндер бағанынан берілген корреляция еселігінің шамасына жуық тек артық емес шама ізделінеді. Сәйкес жолдың сол жағынан n көрсеткішін табамыз. Міне осы, корреляция еселігінің қажетті дәлділігін және өлшеуге, санауға, есептеуге ж.т.т. артық еңбек шығарудың алдын алатын, қажетті ізделініп отырған зерттеудегі белгілер жұп саны болады.

20-кесте - Мәнi 5%-ды деңгейдегi корреляция еселігінің ауытқулық маңызы

n	r	n	r	n	r
	0,997		0,468		0,325
	0,950		0,456		0,304
	0,878		0,444		0,288
	0,811		0,433		0,273
	0,754		0,423		0,250
	0,707		0,413		0,232
	0,666		0,404		0,217
	0,632		0,396		0,205
	0,602		0,388		0,195
	0,576		0,381		0,159
	0,553		0,374		0,138
	0,532		0,367		0,113
	0,514		0,361		0,098
	0,497		0,355		0,088
	0,482		0,349		0,062

Корреляция еселігі 0,68 болған, біздің мысалымыз үшін кестеден жуық ауыспалы мәнін табамыз. Ол 0,666 тең. Оған n=9 сәйкес келеді. Міне, сол осы талдаудың қажетті ең аз саны болып табылады. Бірақ бұл абсолютті дәл болған болжам емес. Ең дұрысы, ықтималдысы болар. Осыған ұқсас зерттеулерде біршама кепілдік үшін шамамен 1/4 - 1/3 бөлігіндей үстеме жасалынады. Айтайық, 9 санына 3 санын қосудың мәні бар. Соңында, біздің мысалымызда, қалай болғанда да ұқсас климат жағдайында (жылдық жауын-шашынға байланысты астық дақылдарының өнімділік деңгейі) жұмысты 12-і жылдық нәтижесі бойынша жүргізуі керек деген тұжырымға келеміз. Зерттеу жұмысы іссанасында корреляция еселігі 0,33-тен (яғни корреляция дәрежесі әлсіз де) төмен және іздестіріп отырған таңдау саны 20-30-дан кем емес жұп болса есептеуді одан әрі жүргізбейді. Мұндай жағдайда таңдауды көбейту (арттыру) зерттелініп отырған белгілердің арасында жоғарырақ байқалатын байланысты ашады деп күтуге болмайды. Бірақ студенттерге машықтану үшін корреляция еселігінің шамасына қарамай барлық есептеулерді толық аяқтаулары керек.

Дата добавления: 2017-02-01