
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Гражданское право 5 страница
|
|
|
|
2. Корреляциялық тор жасау. Корреляциялық тор бұл бастапқы деректерді (яғни талдаудағы белгілердің жұп мәндері) кластарға бөліп орналастырылатын кесте.
Корреляциялық торда жолдар мен бағандардың саны кластардың (К) санына немесе нақтырақ, 23-кестедегі жол санына байланысты анықталады. 23-кестенің барлық сандары 24-кестенің белгіленген жолдарына және бағандарына толығымен көшірілгенін байқау жеңіл. Сонымен, 24-кестені дайындамастан бұрын, оның көлемімен мұқият танысып, 23-кестенің жолдарындағы және бағандарындағы барлық деректерді орналастыру керек екенін ескерген жөн. Қисық сызықты корреляция жұмыс істеуді жеткілікті меңгергенде 23-кестесіз-ақ жұмысты тындыруға болады. Яғни, шамаларды кластарға бөлуді және кластардың орташа мәнін есептеуді тікелей корреляциялық торда жүргізуге болады. Бірақ тақырыпты алғашқы игерген кезде осы нұсқаудың 23-кесте пішініне ұқсас, қосымша кесте бәрібір керек.
Корреляциялық тордың пішінін сызғаннан кейін оның ішкі торлары бастапқы дерек кестесінің негізінде толтырылады (21-кестені қараңыз).
Нақты мысалмен түсіндірейік. 21-кестеде белгілердің бірінші жұбы мынадай: Х = 21; У = 0,82. Х белгісі бойынша белгілердің бұл жұбы бірінші класқа (21-46) жатуға тиіс, У белгісі бойынша бұл жұп белгі де бірінші класқа (0,77-0,54) жатқызылуға тиіс. Торда осы кластардың қиылысында сызықтар (штрих) жасалынады. Осылайша 21-кестеде жиналынған, талданылатын белгілердің барлық жұп көрсеткіштерін рет-ретімен торларға орналастырады. Көлденең және тік сызықтардың қосындысы талданатын белгілердің класс бойынша таралу жиілігі f болып табылады. Мұндайда бұрыштағы тік және көлденең қосындылар бірдей болуға тиіс және одан басқа, ол талданылатын белгілердің n жұп көрсеткіштерінің жалпы санына тең болуы тиіс.
Сызықтық таратуларды аяқтағаннан соң У белгісінің кластарының орта мәнін жиілікке (сызықтар саны) көбейтіндісі есептелінеді. Мұндай есептеулер сызықтары бар әрбір торда жүргізіледі. Кластардың орташа мәнінің сызықтар санына көбейту нәтижесі сәйкес торға жазылады. Мысалы, 24-кестенің бірінші жолында үш торда бір бірден сызық бар. Демек, осы торлардың әрқайсысына У белгісінің бірінші класының орташа мәнін, ол біздің мысалымызда 0,86 тең, қою керек. Міне тағы бір мысал. Орташа мәні 1,58-ді бесінші кластың жолында бірден және екіден сызық бар. Ондайда бір сызығы бар торға жай 1,58 саны қойылады. Ал екі сызықты торға осы санның екіге көбейтілген (1,58х2 = 3.16) көбейтіндісі қойылады. Сызықтары бар басқа да торлар осылайша толтырылады.
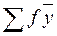 жолындағы сандар тік бойдағы сандардың қосындысынан алынады. Бұл қосындыға f жолының сандарын ешқашан да қосуға болмайды. Соңғы жиынтық бағанда
жолындағы сандар тік бойдағы сандардың қосындысынан алынады. Бұл қосындыға f жолының сандарын ешқашан да қосуға болмайды. Соңғы жиынтық бағанда 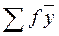 жолының барлық сандары қосылған. Біздің мысалымызда
жолының барлық сандары қосылған. Біздің мысалымызда 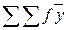 барлық қосындысы 35,9 тең.
барлық қосындысы 35,9 тең.
Соңғы жол – Х мәнінің шегіндегі У мәнінің топтық орташа мәні. Бұл топтық орташа шамалар 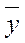 пен белгіленеді және
пен белгіленеді және 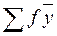 жолының сандарын f жолының сандарына бөліп табады. Мұндайда ең соңғы бағандағы бөлудің нәтижесі,
жолының сандарын f жолының сандарына бөліп табады. Мұндайда ең соңғы бағандағы бөлудің нәтижесі, 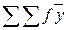 -тің жалпы қосындысын
-тің жалпы қосындысын 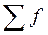 , немесе n-ге талданып отырған
, немесе n-ге талданып отырған 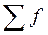 немесе n белгілерінің жұп санына бөлгенде шығатын сан болады. Сонымен, біз У белгісінің орта мәнін аламыз. Кейінгі есептеулерде бұл шамалар
немесе n белгілерінің жұп санына бөлгенде шығатын сан болады. Сонымен, біз У белгісінің орта мәнін аламыз. Кейінгі есептеулерде бұл шамалар 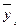 -пен белгіленеді.
-пен белгіленеді. 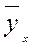 пен
пен 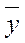 -тің есептелу дәлдігін көпшілік қабылдаған дөңгелектеу ережесін пайдаланып бастапқы деректер кестесіндегі х белгісінің алғашқы көрсеткішіне дейін жеткізеді (21-кестені қарайңыз).
-тің есептелу дәлдігін көпшілік қабылдаған дөңгелектеу ережесін пайдаланып бастапқы деректер кестесіндегі х белгісінің алғашқы көрсеткішіне дейін жеткізеді (21-кестені қарайңыз).
3. Вариацияны есептеу және корреляциялық қатынастарды анықтау. Вариациялық есептеу кестесі корреляциялық тордың негізінде жасалынады. 1, 4, 6, 9 бағандардың сандары 24-кестеден толығымен көшіріледі. Есептеудің жолдары аталған бағандарда көрсетілген. Екінші бағандағы сандар бірінші баған сандарының арифметикалық орташа мәнінің 
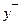 айырмасы. Бұл көрсеткіш те корреляциялық торда есептелінгенін ескертеміз. Біздің мысалымызда ол 1,44-ке тең. 7 бағанның сандары – бұл 6 баған сандарының
айырмасы. Бұл көрсеткіш те корреляциялық торда есептелінгенін ескертеміз. Біздің мысалымызда ол 1,44-ке тең. 7 бағанның сандары – бұл 6 баған сандарының 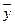 мәнінің айырмасы.
мәнінің айырмасы.
Одан әрі айырымдарды квадраттау және кейінгісін жиілік f көрсеткішіне көбейту жүргізіледі. Содан кейін 5 және 10 бағандарының қосындылары шығарылады.
25-кестедегі есептеулердің дәлділігі, бастапқы деректер көрсеткішіндегі бастапқы көрсеткіштің У дәлдік мәніндей болуы керек. Осы мақсат үшін дөңгелектеу математиканың көпшілік мақұлдаған ережесімен жүргізіледі. Бірақ, мынаны есте ұстаған жөн: егер У көрсеткішінің бастапқы мәні көп жағдайда бірден кем болса, дөңгелектеу мәнді үш цифрға дейін жүргізіледі.
Вариациялану кестесімен жұмыс аяқталғаннан кейін, Х және У көрсеткіштерінің арасындағы қисық сызықты байланыстың деңгейі бағаланатын, корреляциялық қатынастар η ух (грек әрпі «эта») есептелінеді. Есептеу жұмыстарында оңайлатып көрсетуге η рұқсат етіледі. Корреляциялық қатынастарды көпшілік мақұлдаған жүздікке дейін дөңгелетуді қолданып, мына формуламен есептейді:
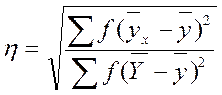
Формула үшін деректер 20-кестеден алынады. Формулаға сәйкес сандарды қойып, табамыз:
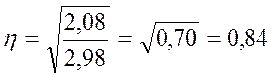
Корреляциялық қатынастар көрсеткіштері бойынша қисық сызықты тәуелділік деңгейі шәкілмен (шкаламен) бағаланады: 0-ден 0,33-ке дейін әлсіз деңгей (байланыс жоқтың қасы); 0,33-тен 0,66-ға дейін – орташа деңгей; 0,66-дан 1,00-ге дейін – жоғары деңгей, 1,00- толық корреляция.
Осы шәкілдің (шкаланың) негізінде, есептелініп табылған корреляциялық қатынастың 0,84 шамасы, талданып отырған қисық сызықтық байланыс жоғары дәрежелі екен деп, қорытынды жасаймыз.
Зерттеліп отырған белгілердің біреуінің екіншісінің өзгергіштігіндегі қатыс үлесін анықтау үшін, корреляциялық қатынастың квадратына тең, детерминация индексін dyf(x) есептейді (есептеу жұмыстарында детерминация индексін қосымша белгілерсіз d әрпімен белгілеуге болады).
dyf(x) = η 2 = 0,842 = 0,70
24-кесте – Корреляциялық тор
| У белгілері | Х белгісі кластар шегіндегі топтық орташа 
| Бөлімнің жиілігі f 
| |||||||
| кластар шегі | кластар
дың орташа мәні 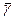
| 21-46 | 47-72 | 73-98 | 99-124 | 125-150 | 151-176 | 177-202 | |
0.77-0.94
0.95-1.12
1.13-1.30
1.31-1.48
1.49-1.66
1.67-1.84
1.85-2.03
f
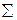 ƒ ƒ 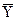    
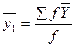
| 0.86 1.04 1.22.2007 1.40 1.58 1.76 1.94 | -0.86 -1.04 -1.22 3.12 1.04 | -1.04 =2.80 -1.58 -1.76 7.18 1.44 | -1.58 -1.76 -1.94 5.28 1.76 | =3.52 -1.94 5.46 1.82 | -1.76 -1.94 3.70 1.85 | -0.86 -1.22 =2.80 =3.16 8.04 1.34 | -0.86 -1.04 -1.22 3.12 1.04 |
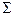 f=25 f=25
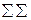 ƒ ƒ 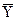 =35,9 =35,9
    
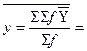 1,44
1,44

|
Ескерту: 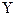 – у белгісі кластарының орташа мәндері
– у белгісі кластарының орташа мәндері
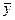 х - х белгісі кластарының шегіндегі топтық орташа белгілер
х - х белгісі кластарының шегіндегі топтық орташа белгілер
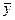 - у белгісінің арифметикалық орташа көрсеткіші
- у белгісінің арифметикалық орташа көрсеткіші
Негізінде детерминация индексін анықтау үшін есептеу жұмыстары қажет емес. Корреляциялық қатынасты есептеген кезде түбір астынан пайда болған нәтиже, басқаша айтқанда, детерминация индекесінің өзі болып табылады. Детерминация индексін анықтайтын формула шын мәнінде, корреляциялық қатынасты есептегендегідей, аралық шамаға кері амал (жүріс) болып табылады.
Детерминация индексінің көрсеткішінің негізінде, Х белгісінің У белгісіне әсері, барлық әсердің 0,70 немесе 70 % тең деп қорытынды жасаймыз.
4. Корреляциялық қатынастардың дәлдігін бағалау.
Корреляциялық қатынастардың дәлдігін бағалаудың ең сенімді тәсілі болып Фишер критерийімен бағалау саналады. Ол үшін алдымен Fф іс жүзіндегі көрсеткіші мына формуламен есептеледі:
d (n – K)
 Fф =
Fф =
(1 – d) (K – 1)
Математикалық мәнде бұл формула Фишер критерийінің өрнегі болып табылмайды. Осы жағдайда Фишер критерийі таза шартты түрде алынған, себебі формуламен есептелгеннен кейінгі нәтиже оған шамасы бойынша сәйкес келеді. Осы талдауды жалғастыра отырып, формулаға сандық мәндерін (есептеу жүздік дәлдікпен жүргізіледі) қоямыз:
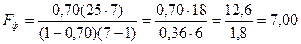
Корреляциянық қатынастың дәлділігін бағалауды алынған нәтижені Фишер критерийінің (Fт) стандартты (кестелі) мәнімен салыстыру арқылы жүргіземіз. Fт мәні арнаулы кестелерден (3-қосымша) ізделінеді. Агрономиялық зерттеулерде 5 % мәнділік дәреже әдетте жеткілікті деп саналады. Сонымен бірге зертханалық және басқа да зерттеулерде, эксперименттерді және өлшеулерді жүргізуге дәлділікті көтеру қолайлы болады, сондықтан, әдетте 1 % мәнділік деңгейі алынады. Осы жұмыста Фишер критерийінің 5% мәнділік деңгейін қолданатын боламыз. Критерийдің кестелік мәнін табу үшін алдымен формуламен еркіндік дәрежесінің сандарын анықтаймыз:
ν1 = К – 1 = 7 – 1 = 6;
ν2 = n – К = 25 – 7 = 18.
Кестеде ν1 еркіндік дәрежесінің сандары бойынша бағаны, ал ν2 еркіндік дәрежесінің сандары бойынша жолы ізделінеді. Біздің мысалымызда соңғы формула бойынша жүргізілген есептеу сәйкес 6 санымен белгіленген бағанды және 18 санымен белгіленген жолды табамыз. Баған мен жолдың қиылысынан 2,66 санын таптық. Міне, осы Fт-ның стандартты мәні.
Корреляциялық қатынастардың шамасы η жеткілікті дәл деп санайды, егер Fф ≥ Fт болса. Олай болмаса корреляциялық қатынастардың шамасы дәл емес деп саналады: ол талданған көрсеткіштердің коррелятивтік байланыс дәрежелеріне шынында да, көп жағынан сәйкес келмеуі мүмкін. Біздің мысалымызда, жоғарыда есептегеніміздей, Fф = 7,00 тең. Бұл (2,66) кестелік мәннен біраз артық. Осыған корреляциялық қатынас әбден дәл деген қорытынды жасаймыз.
Корреляциялық қатынастардың детерминация индексі квадраттарының қатесін мына формуламен есептейміз:
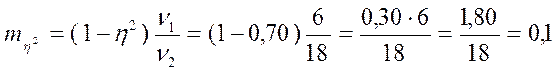
Корреляциялық қатынастардың ақиқаттылығын мына формуламен бағалайды:
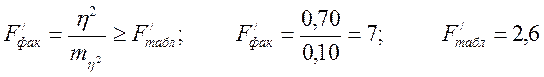
7,00 ≥ 2,66, демек осы сенімділік дәрежесінде Х факторының өзгеруі У факторының өзгеруіне анық әсер етеді.
Корреляциялық қатынастардың, яғни Х және У көрсеткіштерінің талданатын жұптарының дәлділігін бағалау санын, таңдамаларды n бағалаумен аяқталады. Мұндай бағалау әсіресе корреляциялық қатынастардың шамалары жеткілікті дәлдікке жеткенде, алдымен n санының жеткіліксіздігінде, ерекше мәнге ие болады. Дәлділікті арттыру үшін Х пен У-тің жұп сандары бойынша байқаулар көлемін кеңейту қажет болады. Корреляциялық қатынастың жеткілікті дәлдігінде, бақылау көлемінің тым артық болатыны да кездеседі.
Қажетті ең аз таңдама n мына формуламен есептеледі:
Fт (1 – d) (K – 1)
 n ' = + K
n ' = + K
Бұл формуланың барлық көрсеткіштері бізге белгілі. Сандарын қойып табамыз:

n´-нің нақты шамасы тек бүтін сан болуға тиіс, сондықтан формуламен есептеудің нәтижесі бүтін санға және ондық белгісіне қарамай міндетті түрде үлкен жағына қарай дөңгелектелінеді.
Жоғарыдағы ең аз таңдаманы есептеуге келтірілген формула нысаналық мәнде екенін айтқанымыз жөн. Сондықтан, ұқсас зерзаттардың (объектілердің) корреляциялық талдауында осындай формула пайдаланылатын болса, қажетті дәлділіктің кепілі үшін қажетті ең аз таңдаманың есептелінген шамасын біразырақ, айтайық, 25-30 пайызға арттырып пайдалану керек. Айтайық, талдап отырған мысалымызда n´ = 14 теориялық ең аз мәнде, іс жүзіндегі таңдаманың көлемін ең аз деңгейде талданатын 18-19 белгілер жұбын алу керек.
Зерттеу жұмыстарының іссанасында (практикасында), егер корреляциялық қатынастар 0,33-тен (яғни корреляция дәрежесі әлсіз де) төмен болса және таңдаманың бастапқы саны 20-30 жұптан кем болмаса, есептеулерді одан әрі жүргізбейді. Мұндайда, таңдаманы арттыру (көбейту) зерделенетін белгілердің арасындағы байланыстың байқалатындай жоғарғы дәрежесін табуға көмектеседі деп сену қиынға соғады. Бірақ, студенттерге біз іссаналық дағды үшін есептелінген корреляциялық қатынастардың шамасына қарамай, барлық есептеуді соңына дейін жүргізгендері дұрыс.
5. Қорытындыны қалыптастыру. Есептеулер аяқталғаннан соң сіздер- студенттер қисық сызықты коррелятивтік байланыстың және оның дәлділігін таңдама көлемінің бағасымен бірге теріп, жазбаша қорытынды жасайсыздар.
Әр түрлі мысалмен қорытындыны тұжырымдаймыз.
1. Корреляциялық қатынастардың ηух = 0,84 шамасына сәйкес талданған белгілердің арасында қисық сызықты коррелятивтік байланыс жоғарғы дәрежеде.
2. Детерминация критерийіне dуf (х) = 0,70 сәйкес, Х белгісі У белгісіне барлық бар ықпалдардың 70 пайыз көлемінде әсер етеді.
3. Критерийдің іс жүзіндегі мәні Fф = 7,00 бойынша стандартты (кестелі) мәнінде Fт = 2,66 корреляциялық қатынастардың шамасының дәлділігі және детерминация индексі әбден жеткілікті.
4. Жұмыс көлемін азайту үшін, осындай ұқсас зерттеулерде іс жүзіндегі бақылау көлемі n = 25, n´ = 14 теориялық ең аз мәнде, соңғы нәтиженің дәлділігіне ешбір зиянсыз 18-19-ға дейін азайтылуы мүмкін.
ІХ. НҮКТЕЛІК СЫЗБАКЕСТЕЛЕР (ГРАФИКТЕР)
1. Алғашқы түсініктер
Зерделінетін белгілердің арасындағы корреляция нүктелік сызбакесте (график) түріндегі көрнекі бейнеге ие болуы мүмкін. Нүктелік сызбакесте қалай салынады? Абсцисс өсіне сызықты шамамен (мөлшермен) белгілі бір масштабта X белгісінің мәндерін, ал ордината өсіне У белгісінің мәнін саламыз. Осы өстер қамтыған аудан, корреляциялық талдауға сәйкес корреляциялық өріс деген атау алды. Енді корреляциялық талдауда зерделінетін белгілердің әрбір жұбын координат нүктелері түрінде елестетіп көрейік. Бұл коррелятивтік байланыстырды зерттеу кезіндегі барлық бастапқы материалдарды тек сан түрінде ғана емес, сонымен бірге корреляция өрісі шегінде нүктелер тізбегі түрінде бейнелеуге болады деген сөз. Осылай көрнекі бейнелеу нүктелік сызбакесте болып табылады.
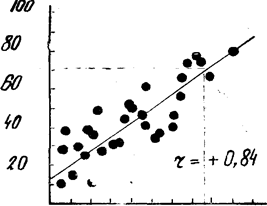
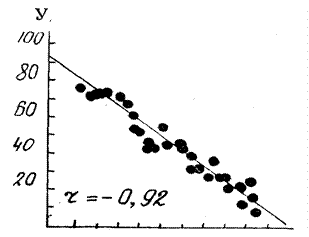
Нүктелік сызбакесте нүктелердің орналасу сипаты бойынша айтарлықтай коррелятивтік байланыстардың барын немесе жоғын және олардың түрлері жөнінде пікір айтуға болады. Тура сызықты байланыс айтарлықтай болғанда нүктелік сызбакестедегі нүктелер тура сызыққа ұмтылады. Егер тура сызықты коррелятивтік байланыс өзінің бағыты бойынша тура болса, онда нүктелер сызығы, координат өстері қалыптастырған бұрыштан шығады (немесе соған жақын), нүктелер сызығы әр түрлі шамада биссектрисаға жақындағандай болады (9-сурет). Кері тура сызықты коррелятивтік байланыста нүктелер сызығы координаттардың екі өсінің қилысына бағытталынады да, үшбұрыш құрағандай болады (10-сурет).
Зерттелетін белгілер арасында қисық сызықты байланыс болғанда коррелятивтік өріс қисық сызық түрінде құрылады (11-сурет). Мұндайда, қисық сызықты тәуелділік неғұрлым күштірек білінсе, нүктелерден соғұрлым анық білінетін қисық сызық көрінеді.
Түзу сызықты, сондай-ақ қисық сызықты байланыстар әлсірей бастаған сайын, нүктелік сызбакестедегі нүктелердің жүйелілігі (реттілігі) жоғала бастайды. Коррелятивтік байланыстардың орта дәрежедегі байланыстарында нүктелердің орналастыруында белгілі бір тәртіпті іздеп табу қиынға соғады. Коррелятивтік байланыстың әлсіз дәрежесінде нүктелер коррелятивтік өріс шегінде қалай болса солай, ретсіз жатады.
 Х
Х
|
9-сурет Тура бағыттағы түзу сызықты коррелятивтік байланыстың нүктелік сызбакестесі
0 20 40 60 80 100
10 - сурет. Кері түзу сызықты коррелятивтік байланыстың сызбакестесі
Ғылыми-зерттеу жұмыстарында нүктелік сызбакестелердің маңызы зор. Олардың маңыздылығы мынада:
1. Нүктелік сызбакестелер ғылыми есепте және ғылыми ақпаратта көрнекі материал болып табылады. Диаграммамен бірге олар зерттеу барысында табылған (ашылған) кейбір заңдылықтарды және құбылыстарды көріп қабылдауға мүмкіндік береді.
2. Нүктелік сызбакестелер, есептеусіз-ақ, алдын ала коррелятивтік байланыстардың бар-жоғын, олардың түрлері мен бағыттарын білуге мүмкіндік береді. Есептеуге кіріспей тұрып, бастапқы цифрлық материалдарды, яғни белгілер жұптарын нүкте түрінде корреляциялық өріске салуға (таратуға) болады. Бұл жұмыс корреляция еселігін немесе корреляциялық қатынастарды есептеумен салыстырғанда еңбекті және уақытты азырақ талап етеді. Сонымен бірге, бастапқы сандар көрсеткіші бойынша, әсіресе зерделінетін көрсеткіштер жұбы көп болғанда, коррелятивтік байланыстың бар-жоғы және олардың сипаты жөнінде болжау өте қиын. Зерттеушінің алдынан – корреляция еселігін, әлде корреляция қатынасын есептейін бе деген сұрақ туындайды. Нүктелік сызбакесте бұған анық жауап береді, ол жөнінде жоғарыда айтқанбыз, себебі, нүктелердің орналасу сипаты айтарлықтай коррелятивтік байланыстың барын және олардың сипатын анық көрсете алады. Зерттеушіні алдымен байланыстың күшті дәрежелілігі мүдделендіреді (қызықтырады). Егер зерттеу жұмысының өн бойында нүктелік сызбакестеде нүктелер не тура, не қисық сызыққа жақындамай, шашылып орналасса, коррелятивтік байланыстың шамасын іздеп, есептеуге кірісудің қажеттілігі жоқ.
3. Корреляциялық талдаудың қиссынды жалғасы – регрессиялық талдау. Оның іссаналық мақсаты – факторлық X белгісінің шамасы бойынша нәтижелі У белгісінің шамасын болжау. Мысалы, астық дақылдарының өнімділігінің шаруашылық, аудан немесе облыс көлеміндегі жазғы жауын-шашын жиынтығымен коррелятивтік байланысы, теориялық қызығушылықтан (мүдделіліктен) басқа, іссаналық мәні де болуы мүмкін: ең ықтималды өнімділікті егін жиналғанға дейін болжауға болады. Сонымен бірге, регрессиялық талдау, әсіресе қисық сызықты байланыстарды, есептеу жұмысында күрделі және қолайсыздау болатынын (екенін) ескерген жөн.
11 - сурет. Қисық сызықты байланыстың
нүктелік сызбакестесі
Нүктелік сызбакестенің көмегімен, регрессия талдауынсыз және есептеу жұмысынсыз-ақ, У белгісінің нәтижелі шамасын болжауға болады.
|
|
|
|
|
Дата добавления: 2017-02-01; Просмотров: 70; Нарушение авторских прав?; Мы поможем в написании вашей работы!