Гражданское право 6 страница

Егер, нүктелік сызбакесте бойынша және регрессиялық талдау көмегімен болжауды салыстырсақ, нүктелік сызбакесте айтарлықтай дөрекі аспап екенін мойындауымыз керек. Сонымен бірге, биологиялық және агрономиялық зерттеулерде көптеген жағдайда болжаудың жоғары дәлділігі талап етілмейді. Мысалы, бізді өнімділіктің жарты центнерге дейін дәлділігі қанағаттандырады, тіпті көптеген жағдайда бір центнерге дейінгі дәлдік те. Тағы бір мысал. Гербицидпен жүргізілген зерттеулерде арамшөптерді басып тастау мүмкін қателігімен 5, тіпті 10 % болжамды тиімді санайды.

2. Нүктелік сызбакестелерді орындау жағдайы.

Нүктелік сызбакестелерді бейнелеу масштабы еркін таңдалады. Бірақ зертханалық іссана жағдайында өстердің сызықтық шамасы 10 сантиметрден болғаны қолайлы. Торлы дәптердің 2 торын 1 сантиметрге балап алады. Әр өс сантиметрмен белгіленеді. Әр бөліктің шамасы (ұзындығы) зерттелініп отырған материалдық сандық көрсеткішінің көлеміне байланысты анықталады. Айтайық, мысалы, корреляциялық талдауда X белгісі ретінде мәдени өсімдіктердің 1м²-дегі сабақ жиілігінің бітіктігі 60-тан 230-ға дейнгі сабағы зерделенеді. Осындайда дөңгелектеу үшін абцисс өсінде басқыштаушылықты (градациялауды) 40-тан бастап 240 санымен аяқтауға болады. Сонда 10 бөлік болады, ал әр бөлік 20 сабаққа тең келеді. Осыған ұқсас басқыштаушылық У өсі бойынша да жүргізіледі. Әрбір өсті нөлдік бөліктен бастаудың қажеті жоқ, егер зерттеп отырған материалдың ең аз сандық көрсеткіші нөлден алшақ болса. Бірақ біздің оқу сабақтарымызда абстракты бастапқы көрсеткіштер координат өстерінде әр бөліктің бағасы 10 бірліктен (яғни 1см) болып басқыштаушылық нөлден жүзге дейін, болғанда жақсы орналасады.

Корреляциялық өріске нүктелер зерттелетін белгілердің әр жұбының сандық көрсеткіштеріне қарай орналастырылады. Егер сандық көрсеткіштер шәкілдің (шкаланың), басқыштаушылықтың сандарымен толық үйлеспесе, онда нүктелердің аралықтары көзбен мөлшерленеді. Мұндайда миллиметрлік қағазбен жұмыс істеу жеңілге түседі. Жақсы көрінуі үшін нүктелердің көлемі диаметрі 3 мм (шырпының күкірт басындай) дөңгелекке дейін ұлғайтылады.

Корреляциялық өріс шегінде нүктелерді орналастырып болғаннан кейін коррелятивтік байланыстың дәрежесі, оның сипаты және бағыты жөнінде белгі қойылады. Корреляциялық таладаулардың тақырыбында зерделенгендей, коррелятивтік байланыс дәрежесінің тура сызықты байланыстарында көрсеткіш болып корреляция еселігі саналса, онда қисық сызықты байланыстарда корреляциялық қатынастар болады. Осыған байланысты тура сызықты корреляцияның нүктелік сызбакестесінде байланыс бағытына сай корреляция еселігі плюспен немесе минуспен көрсетіледі, ал қисық сызықты байланыстың нүктелік сызбакестесінде корреляциялық қатынастар көрсетіледі (9, 10, 11 – суреттерді қараңыз).

Коррелятивтік байланыстар жоғары дәрежелі болғанда нүктелік сызбакесте номограмма сияқты X белгісінің белгілі шамасындаУ белгісінің ықтималды шамасын жорамалдауға пайдаланылуы мүмкін. Ол үшін нүктелік сызбакестеде регрессияның теориялық сызықтары сызылады. Толық коррелятивтік немесе соған жуық байланыс болғанда регрессияның теориялық сызықтары іс-жүзінде барлық нүктелерді қосады. Бірақ кездейсоқ факторлардың үдемелі әсері артқан сайын нүктелер әр түрлі шамада қолайлы (өте жақсы) орнынан алшақтай бастайды. Мұндайда нүктелер регрессияның эмпириялық сызықтары деп аталынатын сынық сызықтармен ғана біріктірілуі мүмкін.

Регрессияның эмпириялық сызығы зерделеніп отырған белгілердің байланыстарындағы заңдылықтарды ғана емес, сондай-ақ кездейсоқтыларды да бейнелейді. Бірақ біз болжау мақсатында кездейсоқтыларға ғана сүйене алмаймыз, себебі бізді алдымен болжауланатын белгілердің ең ықтималды заңды шамалары қызықтырады. Міне, сондықтан болжау мақсатына үлкен деңгейде регрессияның тек заңдылықты бейнелейтін, теориялық сызығы ғана шүбәсіз жауап береді.

Зерделеніп отырған белгілердің коррелятивтік байланыстары толық болған жағдайда, регрессияның эмпириялық және теориялық сызықтары үйлеседі. Бірақ толық коррелятивтік сызықтардан ауытқыған сайын бұл сызықтар үйлесуден көбірек ауытқи бастайды. Мұндайда регрессияның теориялық сызығын көзбен болжап, оның екі жақтағы нүктелерінің орнын теңестіретіндей етіп анықтайды.

Регрессия сызығын көзбен бейнелеу қашанда белгілі бір шамада өззаттық (субъективті) және орындаушының тәжірибелілігіне тәуелді болады. Күрделі жағдайда регрессия сызығын жіпті қолданып немесе мөлдір (калька) қағазға сурет үлгісін салып өлшеуге болады. Тура сызықты байланыстар үшін регрессияның теориялық сызығы тура сызық түрінде болады. Соған қарамастан тура сызықты байланыстарда сирек болсадағы регрессия сызығының біраз қисықтығы байқалады. Әңгіме мынада, тура сызықты және қисық сызықты байланыстардың арасында айқын шекара жоқ. Кейбір жағдайларда, сызықтық критерийді есептегенде белгілер арасындағы, байқалған байланыстарды қай түрге жатқызу керек деген сұраққа жауап іздеуге тура келеді. Ал, біздің іссаналық (практикалық) сабақтарда ондай міндет тұрған жоқ. Сондықтан тура сызықты корреляциялық нүктелік сызбакесте үшін регрессияның теориялық сызығын түпнұсқалық (нақ) түзу ретінде бейнелеу керек.

Қисық сызықты корреляцияның нүктелік сызбакетесінде регрессияның теориялық сызығы параболаға жуықтауы керек. «Қисық сызықты» тақырып тапсырмасы бойынша нақ осындай байланыс түрі ескерілген. Кейде нүктелердің орналасуымен параболаның бұрыш тәрізді сүйір ұшы пайда болады (жасалынады). Нақты қисық сызықты байланыстарда мұндай айқын ауысу болмайтынын ескерген жөн. Сондықтан қисық сызықты байланыстардың регрессия сызығы жатық сипатта, ешбір бұрышсыз болуға тиіс. Егер нүктелік сызбакестеде бұрыш пішіні байқалынатын болса, оны кездейсоқтықтан пайда болған деп мойындап, қабылдау керек.

Регрессияның теориялық сызығын пайдаланып нүктелік сызбакестемен болжау техникасы былай іске асырылады. Ордината өсінде X белгісінің мәніне сәйкес нүкте анықталады да, сонымен У белгісінің ең ықтимал мүмкін мәні болжауланады. X белгісінің табылған нүктесінен регрессияның теориялық сызығына қиылысқанша тік сызық жүргізіледі. Содан кейін осы қиылыс нүктесінен солға қарай үзілме (пунктер) көлденең сызық салынады, яғни ордината өсіне параллель және абсцисаға тіктеме (перпендикуляр) сызық сызылады. Үзілме сызықтың абсцисса өсімен қилысқан нүктесінде У белгісінің болжамды мәні орналасады. У белгісінің сандық мәнін межесызықтың басқыштаушылығына (шкала градуирования) сүйеніп анықтауға болады. Мысалы, 9-шы сурет бойынша, X белгісі 77-ге тең болғанда У белгісінің болжамды мәні 70-ке тең болады.

1. Келтірілген үлгілерге (суреттер) және жоғарыдағы орындау жағдайларына сүйеніп, әр студент «Тура сызықты корреляция» және «Қисық сызықты корреляция» тақырыптары бойынша берілген жеке тапсырмалардың деректеріне сай екі нүктелік сызбакесте салады.

2. Жоғары дәрежелі коррелятивтік байланысы бар сызбакестелерде регрессияның теориялық сызықтары сызылады. Тура сызықты корреляция сызбакестесінде регрессияның теориялық сызығы түзу (тура), ал қисық сызықты корреляция сызбакестесінде парабола тәрізді екенін ескертеміз.

3. Оқытушы берген X белгісінің үш мәні бойынша, коррелятивтік байланыс дәрежесі жоғары сызбакестелерде, тура сызықты және қисық сызықты корреляциялары бойынша, У белгісінің мәніне болжау жүргізу керек. Болжау нәтижесі бойынша жазбаша сипаттама жасалынады.

Жазба пішінің үлгісі:

Тура сызықты корреляцияда

1) Х=11; У=8

2) Х=42; У=33

3) Х=85; У =68.

Қисық сызықты корреляцияда

1) Х=11; У=10

2) Х=42; У=84

3) Х=85; У=73.

Х. РЕГРЕССИЯ (шегіну, кері кету)

1. Негізгі түсініктер.

Өзара тәуелді құбылыстарды зерделегенде математикалық статистика әдістерін қолдану, осы өзара байланысты аса тереңірек болжауға мүмкіндік береді. Корреляциялық талдау байланыс тереңдігінің бірлік үлесін және оның бағытын (оң, теріс) анықтайды. Регрестік талдау (латынның regressio – кері кету, шегіну, кері шегінушілік) сызықтың регрессияның теңдеуінің көмегімен тәуелсіз айнымалы Х-тің өзгеруінен тәуелді айнымалы У –тің өзгеру сипатын анықтауға мүмкіндік береді. Регрессиялық талдауға тура сызықты корреляциялық еселігін анықтағаннан кейін кірісу ең қолайлы саналады (63 және 67 беттердегі 18-кестені қараңыз). 18-кестеде астық дақылдарының жылдық жауын-шашын жиынтығына байланысты өнімділігі келтірілген. Есептеулер, аталған екі құбылыс арасында, r =+0,68 ± 0,26, F_факт > F_табл, жоғары дәрежелі тура коррелятивтік байланыс бар екенін көрсетіп отыр. Зерделеніп отырған құбылыстардың осындай өзара байланысы, математикалық статистикада тура сызық теңдеуі түрінде өрнектеу белгіленген [5]

У_Т = а + bх,

мұнда У_Т – У-белгісінің теориялық мәні;

а – бос мүше;

в – регрессия еселігі;

х – тәуелсіз айнымалы шама.

«Регресті талдау» тақырыбын орындау үшін бастапқы деректер болып жеке шифр бойынша тура корреляция еселігін есептеу нәтижелері саналады (65 беттегі 19-кестені қараңыз). Алдыңғы есептеулердің нәтижесін пайдаланып әр студент, а бос мүшенің, b регрессия еселігінің және регрессия теңдеуінің бүтіндей сандық мәнін табады.

3.Жұмыс барысы

Регрессия еселігін есептеу. Талдап отырған мысалдың (18-кесте) регрессия еселігін мына формулалар бойынша табамыз:

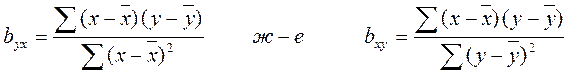
Әріптік белгілердің түсіндірмелерін тура сызықты корреляция тарауынан қараңыз.

Формулаларға 63-беттегі 18-кестеден әріптік белгілердің сандық мәндерін қоямыз және шешеміз:

Бос мүшені есептеу. Регрессия теңдеуінің бос мүшесін мына формуламен табамыз:

.

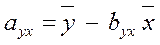18-кестеден сандық мәндерін қойып, шығарамыз:

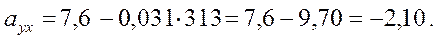
Бақылау үшін бос мүшені регрессияның мына теңдеуімен табамыз:

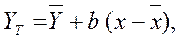
Сандық мәндерін қойып, табамыз:

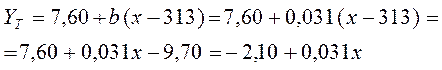
Талданып отырған көрсеткіштер үшін регрессияның бастапқы теңдеуі мынадай түрде болады:

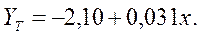
Тексеру амалдары немесе регрессия еселіктерін есептеудің екінші тәсілі. Егер корреляция еселігі есептелінген болса, b_yx және b_xy регрессия еселіктерін төмендегі формулалармен табуға болады:

мұнда S_y және S_x Y және Х айнымалы шамалардың орта квадратты стандартты ауытқулары.

Табамыз:

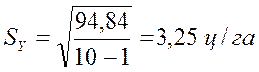
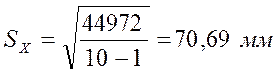
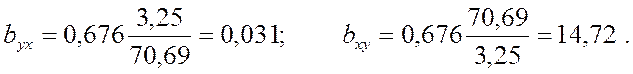Корреляция еселігін одан да дәлірек есептеу үшін үтірден кейін үш белгі алу керек.

Корреляция еселігі - квадрат түбірді регрессия еселігіне көбейткенге тең:

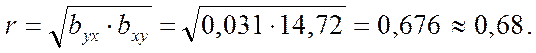
Осыдан регрессия еселігі дәл табылған деген қорытынды жасаймыз.

У_Т теориялық (есептік) көрсеткішін есептеу. Теориялық (есептік) көрсеткіштер үшін 18-кестенің 2-ші бағанының көрсеткіштерін алып, регрессия теңдеуіне қоямыз және есептейміз. Мысал ретінде 18-кестенің 2-ші бағанының бірінші жолының көрсеткіштерін аламыз.

Y_Т= -2,1+0,031 · 201= -2,10 + 6,23= 4,13 ц/га

Астық дақылдарының теориялық өнімділігі х =201 миллиметрде 4,1 ц/га, ал іс-жүзіндегі өнімділігі 2,3 ц/га болғанда. Осыған ұқсас тәсілмен барлық он жол үшін теориялық көрсеткіштерін есептейміз және оларды 26-кестеге толтырамыз. Ескертеміз: жеке тапсырмада х және у мәндері 28-ге тең (65 беттегі 19-кесте).

26-кесте- У көрсеткішінің теориялық мәнін есептеу (Вольф В.Г., 160-бет)

№ р/р	Жылдық жауын-шашын-ның қосынды-сы, мм* (Х)	(0,031 х)	Теориялық көрсеткіші УТ = а+bх (УТ=-2,10+0,031x)	Іс-жүзіндегі көрсеткіші* У, ц/га	УТ-ң У Ф-н ауытқуы (УТ –У)	Ауытқу квадрат-тары (УТ–У)
		6,23	4,1	2,2	-1,9	3,61
		7,13	5,0	10,0	-5,0	25,00
		9,14	7,0	6,8	+0,2	0,04
		11,07	9,0	11,2	-2,2	4,84
		12,06	10,0	10,3	-0,3	0,09
		11,66	9,6	7,6	-2,0	4,00
		9,30	7,2	6,5	+0,7	0,49
		8,40	6,3	6,3	0,0	0,0
		8,96	6,9	3,3	+3,6	12,96
		12,96	10,9	11,8	-0,9	0,81
* Берілген шифр бойынша есептеулер жүргізгенде дұрысы бағандарды тәуелсіз айнымалы Х және тәуелді айнымалы У деп атау.	S=-7,8	S=59,13

Регрессия еселігінің елеулі критерийін есептеу. Регрессия еселігінің b_yx елеулі критерийін есептеу үшін 26-кестенің есептелінген нәтижелерін пайдаланамыз және формула бойынша квадраттық орта ауытқуларын табамыз:

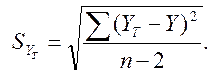
26-кестеден әріптік белгілердің сандық мәндерін қойып, табамыз:

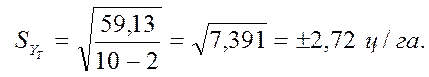
Тәуелді айнымалы У-тің іс-жүзіндегі және есептелінген теориялық мәндерінің арасында айырмашылық неғұрлым аз болса, соншалықты квадраттық орташа ауытқулары азырақ, байланыс тереңірек және регрессия теңдеуі дәлірек болатынына көңіл қойған жөн болады.

Квадраттық орташа ауытқуларын біле отырып, регрессия еселігінің қатесін m_b табамыз. Ол тең болады:

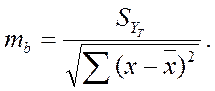
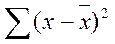-тің сандық мәнін 26-кестеден алып қоямыз және табамыз:

t_факт, анықтаймыз, ол тең болады:

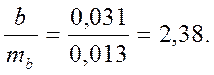
Стьюдент критерийін, (t_кест.) 4-қосымша бойынша еркін дәреже ν = n–2 = 10–2 = 8 болғанда, ол 2,31-ге тең екендігін табамыз. t_факт және t_кест., салыстырамыз, 2,38>2,31, яғни t_факт > t_кест.

Регрессия еселігін елеулі деп қорытынды жасаймыз.

Ү_т теориялық (есептеулік) көрсеткіші үшін сенімді аралықты есептеу. Квадраттық орташа ауытқу 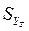анықталынды, ол 2,72 ц/га тең. Теориялық көрсеткіштің абсолютті қатесін табамыз:

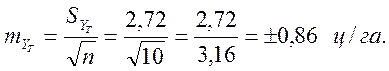
2 – қосымша бойынша Стьюдент критерийі (t_кест.) еркін дәрежесі ν = n–2 = 10–2 = 8 болғанда, ол 2,31 тең болады. Ү_т теориялық көрсеткіші үшін сенімді аралығы тең болады:

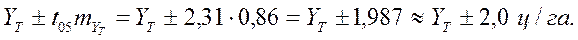
Ү_т көрсеткішінің теориялық (есептік) дәлділігін бағалау. Есептеу үшін әріптік белгілердің сандық мәндерін 26-кестеден алып, формулаға қоямыз:

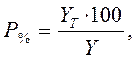
мұнда Р_% - теориялық көрсеткіштің дәлділігі, %.

Ғылыми мақсат үшін У көрсеткішінің барлық теориялық дәлділігін анықтау керек. Оқу мақсатында үш есептеумен шектелуге болады. Ол үш екі шеткі және бір ортаңғы көрсеткіштерді, айтайық, талдап отырған мысалдың 1, 2, 3 жолдарын алып, 26-кестеден әріптердің сандық мәнін формулаға қойып, табамыз:

1-жол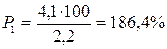
2-жол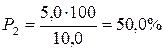
3-жол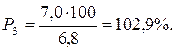

Есептеулер, теориялық көрсеткіштердің дәлділігі өте өзгермелі екенін, көрсетіп отыр. 1-ші және 2-ші жолдар үшін дәлдік көрсеткіштері сөзсіз тиімсіз, ал 3-жол үшін дәлділік жақсы.

Ү_т көрсеткіш дәлділігінің осылай өзгергіштігі, өсінді кезіндегі жауын-шашынның өте-мөте бір қалыпты түспеуімен және өсімдіктің өсуінің қиын-қыстаң кезеңімен тұстас болмауымен түсіндіріледі, демек, астық дақылдарының өнімділігіне елеулі әсер ете қоймайды. Осыны талдап отырған мысалдан байқауға болады. Басқа жағдайларда байланыс тығыздау болуы мүмкін, ал тәуелсіз айнымалының Х ықпалы уақыт бойынша созылыңқы емес. Мұндайда теориялық көрсеткіштің дәлділігі жоғарырақ болады.

1. Тура сызықты оң регрессияның теңдеуі Y_Т = а + bх бос мүшенің а = -2,10 сандық мәнін және регрессия еселігін b = 0,031 деп қойғанда мынадай түрге енеді: Y_Т = -2,10+0,031x.

2. t_факт > t_кест. болғанда регрессия еселігінің қатесі 0,013 тең. Регрессия еселігі мәнді.

3. Ү_т көрсеткішінің есептелінген квадратты орта ауытқуы ±2,72 ц/га, абсолютті қатесі - ±86ц/га, ал сенімді арақашықтығы Y_Т ±2,0ц/га тең.

4. Талдап отырған мысал үшін Ү_т көрсеткішінің есептеленген дәлділігі 50-ден 186 %-ға дейін өзгереді.

1. Вольф В.Г. Статистическая обработка опытных данных. –М.: Колос, 1966.-255 с.

2. Гладских А.И., Льянов Х.-М.М. Математико-статистическое моделиро -вание в агробиологии. –Целиноград: Изд-во ЦСХИ, 1989, -83 с.

3. Гулинова Н.В. Методы агроклиматической обработки наблюдений. – Л.: Гидрометеоиздат, 1974. -151 с.

4 а. Дмитриев Е.А. Математическая статистика в почвоведении. –М.: Изд-во Мос. ун-та, 1972. -292 с.

4 б. Дмитриев Е.А. Математическая статистика в почвоведении. –М.: Изд-во Моск. ун-та, 1995. -320 с.

5. Доспехов Б.А. Методика полевого опыта (с основами статистической обработки результатов исследований). Изд.5-е. –М.: Агропромиздат, 1985. -357 с.

6. Зайцев Г.Н. Математическая статистика в экспериментальной ботанике. –М.: Наука, 1984. -424 с.

7. Иванова В.М. и др. Математическая статистика. Изд-е 2-е. –М.: Высшая школа, 1981. -368 с.

8. Козьмина Н.П. Зерно. –М.: Колос, 1969. -368 с.

9. Лакин Г.Ф. Биометрия. Изд-е 3-е. –М.: Высшая школа, 1980. -294 с.

10. Литтл Т, Хиллз Ф. Сельскохозяйственное опытное дело. Планирование и анализ. Перев. с англ. –М.: Колос, 1981. -320 с.

11. Минкевич Н.И., Захаров Т.И. Математические методы в фитопатологии. –Л.: Колос, 1977. -47 с.

12. Пересыпкин В.Ф. и др. Практикум по методике опытного дела в защите растений. –М.: Агропромиздат, 1989. -175 с.

13. Плохинский Н.А. Биометрия. ­–Новосибирск: Сиб. отд. АН СССР, 1961. -364 с.

14. Терентьев П.В., Ростова Н.С. Практикум по биометрии. –Л.:Изд.ЛГУ, 1977. -152 с.

15.Томилов В.П. Практикум по методике опытного дела. –Целиноград: Изд. ЦСХИ, 1983. -74 с.

16.Томилов В.П. О статистической обработке многолетних данных полевых опытов. Земледелие, 1987, №3, с.48-53.

17. Удольская Н.Л. Введение в биометрию. –Алма-Ата: Наука, 1976, -84 с.

18. Федоров А.И. Методы математической статистики в биологии и опытном деле. –Алма-Ата: Казгосиздат, 1957. –150 с.

19. Шашко Д.И. Агроклиматические ресурсы СССР. –Л.: Гидрометиздат, 1985. - 247 с.

1-қосымша

БИОМЕТРИЯДАҒЫ, МАТЕМАТИКАЛЫҚ СТАТИСТИКАДАҒЫ ТЕРМИНДЕРДІҢ ҚЫСҚАША СӨЗДІГІ

Ақиқаттылық – таңдаулы көрсеткіштер негізінде бас параметрлер жөнінде сенімділікпен айта алады. Ықтималдылық түсінігінде білдіріледі.

Амплитуда – осы таңдама жиынтығындағы белгілердің вариациялық шамасының ең аз (минималды) мәнінен ең көп (максималды) мәніне (вариациялану пәрмені, шегі) дейінгі өзгеруі.

Аралық (интервал) – кез келген зерделінетін көрсеткіштің вариациялық қатарындағы кластардың мәндік екі сандарының арасындағы аралық.

Аргумент – тәуелсіз айнымалы шама (х), оның өзгеруі онымен байланысты тәуелді айнымалы, функция (у) деп аталынатын айнымалы шаманың өзгеруіне әкеледі.

Арифметиқалық орта мән – вариациялық қатардың негізгі сипаттамаларының бірі, тандама жиынтықтардың барлық нұсқалары топтасатын таралу орталығы болып табылады.

Ауытқу – берілген статистикалық жиынтықтың жеке нұсқасынан және шамалық орта арасындағы айырым.

Баға – тандамалы көрсеткіштің белгілі шамасының негізінде берілген бас параметрдің жуық сипаты.

Бас жиынтық – таңдама жиынтығы шығарылатын нақты іс-әрекеттегі барлық зерзаттар (объектілер) жиынтығы. Берілген кешенді жағдайда алуға болатын, барлық мүмкін бақылаулардың көптеген нәтижелерінен тұратын, математикалық статистикадағы абстракты түсінік.

Дата добавления: 2017-02-01