Пояснение к работе

Время выполнения практического задания – 2 часа.

Последовательность выполнения

1. Руководствуясь приведенным теоретическим материалом, ответить на следующие вопросы:

В чем состоит алгоритм поиска путей с минимальным числом дуг?

Какой цикл называется эйлеровым?

Каков критерий существования эйлерова цикла в графе?

Каков критерий существования эйлеровой цепи в графе?

2. Дать определение следующих понятий:

– маршрут в графе (привести пример);

– цепь и простая цепь в графе;

– цикл и простой цикл в графе;

– эйлеровой цепь;

– матрица смежности графа;

– степень вершины графа.

3. Выполнить задания для аудиторных занятий.

4. Выполнить задания для самостоятельной работы.

6.1. Маршруты, цепи, циклы

Маршрутом в графе G = (V, E) (путем в графе D = (V, E)) называется последовательность вершин и рёбер (дуг) вида v ₀, e ₁, v ₁, e ₂,..., v _n-1, e _n, v _n, где v _i Î V, i Î [0, n ], e _i Î E, (v _i-1, e _i), (v _i, e _i) Î I, i Î [1, n ]. Вершины v ₀, v _n называются связанными данным маршрутом (или просто связанными). Вершину v ₀ называют началом, а v _n – концом маршрута. Если v ₀ = v _n, то маршрут называют замкнутым. Число n называется длиной маршрута.

Маршрут, в котором все рёбра попарно различны, называется цепью. Замкнутый маршрут, являющийся цепью, называется циклом (контуром). Цепь, в которой все вершины попарно различны, называется простой цепью. Цикл, в котором все вершины, кроме первой и последней, попарно различны, называется простым циклом.

Примеры: 1. Последовательность v ₁, e ₁, v ₂, e ₃, v ₄, e ₄, v ₃ – маршрут длины 3, соединяющий вершины v ₁, v ₃ в графе G (рис. 11); это простая цепь, так как все ребра и вершины попарно различны.

2. v ₂, e ₃, v ₂ – простой контур длины 1 в ориентированном псевдографе D (рис. 10).

3. v ₁, e ₂, v ₂, e ₄, v ₃ – путь из v ₁ в v ₃ длины 2 в ориентированном псевдографе D (рис. 10); это простая цепь, так как все дуги и вершины попарно различны.

Рис. 10 Рис. 11

6.2. Поиск путей (маршрутов)с минимальным числом дуг

При решении некоторых прикладных задач нередко возникает необходимость найти минимальный маршрут, соединяющий заданные вершины в графе. Приведем алгоритм решения этой задачи. Путь в орграфе D из вершины v в вершину w (v ¹ w) называется минимальным, если он имеет минимальную длину среди всех путей орграфа D из вершины v в вершину w. Аналогично определяется минимальный маршрут в графе G. Алгоритм нахождения минимального маршрута состоит из следующих шагов:

Шаг 1. Помечаем вершину v индексом 0. Затем помечаем вершины, принадлежащие образу вершины v, индексом 1. Множество вершин с индексом 1 обозначаем FW₁(v). Полагаем k = 1.

Шаг 2. Если FW_k(v) = Æ или выполняется k = n – 1, w Ï FW_k(v), то вершина w не достижима из v и работа алгоритма на этом заканчивается. В противном случае переходим к шагу 3.

Шаг 3. Если w Ï FW_k(v), то переходим к шагу 4. В противном случае существует путь из v в w длины k, и этот путь является минимальным. Последовательность вершин

v w₁w₂ …w_k-1w_, где w_k-1 Î FW_k-1(v) Ç D^-1(w); w_k-2 Î FW_k-2(v) Ç D^-1(w_л-1); … w₁ Î FW₁(v) Ç D^-1(w₂) и есть искомый минимальный путь из v в w. На этом работа алгоритма заканчивается.

Шаг 4. Помечаем индексом k + 1 все непомеченные вершины, которые принадлежат образу множества вершин с индексом k. Множество вершин с индексом k + 1 обозначаем FW_k+1(v). Присваиваем k:= k + 1 и переходим к шагу 2.

Пример. Используя предложенный алгоритм, определим минимальный путь из v ₁ в v ₆ в орграфе D, заданном матрицей смежности, представленной в табл. 1.

Таблица 1

	v1	v2	v3	v4	v5	v6
v1
v2
v3
v4
v5
v6

Действуя согласно алгоритму, последовательно определяем FW₁(v₁) = { v_4, v₅ }; FW₂(v₁) = D(FW₁(v₁))\{ v_1, v_4, v₅ } ={ v_2, v₃ };

FW₃(v₁) = D(FW₂(v₁))\{ v_1, v_2, v_3, v_4, v₅ } = { v₆ }. Таким образом, v₆Î FW₃(v₁), а значит (см. шаг 3) существует путь из v₁ в v₆ длины 3 и этот путь является минимальным. Найдем теперь минимальный путь из v₁ в v₆. Определим множество

FW₂(v₁) Ç D^-1(v₆) = { v_2, v₃ } Ç { v_2, v₃ } = { v_2, v₃ }.

Выберем любую вершину из найденного множества, например вершину v₃. Определим далее множество FW₁(v₁) Ç D^-1(v₃) = { v_4, v₅ } Ç { v_4, v_5, v₆ = { v_4, v₅ }. Выберем любую вершину из найденного множества, например, вершину v₅. Тогда v₁ v₅ v₃ v₆ – искомый минимальный путь из v₁ в v₆ длины 3 в орграфе D.

6.3. Эйлеровы графы

Пусть G – псевдограф. Цепь (цикл) в G называется эйлеровой, если она (он) проходит по одному разу через каждое ребро псевдографа G.

Рис. 12

Задача состоит в следующем: найти эйлеров цикл в мультиграфе G (рис. 12). Прежде чем решать задачу о выделении эйлеровой цепи или эйлерова цикла в псевдографе, надо выяснить, существуют ли они. Простейшее необходимое условие их существования, очевидно, заключается в связности G. Ответ на этот вопрос дают приводимые ниже теоремы. Эйлеровым называется цикл, проходящий по каждому ребру графа ровно один раз. Граф, имею-

щий эйлеров цикл, тоже будем называть эйлеровым. В любом эйлеровом графе степени всех вершин чётные.

Пусть по некоторой вершине v цикл проходит k раз. Но так как перед этой вершиной и после неё цикл должен проходить по инцидентным ей рёбрам, то количество рёбер, инцидентных данной вершине, по которым проходит цикл – 2 k. Так как цикл эйлеров – рёбер, по которым цикл не проходит, нет, значит 2 k – степень вершины v.

Если в связном графе степени всех вершин чётные, то в графе существует эйлеров цикл. В ходе доказательства мы дадим алгоритм построения такого цикла. Начнём с произвольной вершины v и будем строить из неё цепь, пока есть возможность её продолжить. Пусть в какой-то момент построения мы находимся в вершине u (не совпадающей с v). Тогда цепь, которую мы построили, проходит по нечётному числу рёбер, инцидентных данной вершине. Степень вершины u чётная, следовательно, есть хотя бы одно ребро, инцидентное вершине u, по которому цепь не прошла – значит её можно продолжить. Следовательно, цепь может закончится только в вершине v. Получим цикл.

В задачах часто возникает необходимость нахождения цепи, проходящей по каждому ребру ровно один раз (снимается требование замкнутости). Такие цепи будем называть эйлеровыми цепями.

Задания

Для аудиторных занятий

1. Задан граф G (рис. 13 а). Найти путь с минимальным числом ребер из вершины v ₁ в вершину v ₆ графа G.

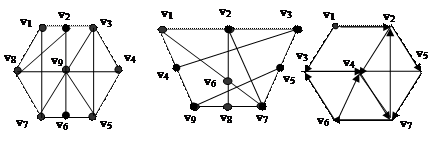а б в

а б в

Рис. 13

2. Для графа G (рис. 13 б) записать матрицу смежности и найти путь с минимальным числом ребер из вершины v ₂ в вершину v ₉.

3. Для орграфа D (рис. 13 в) записать матрицу смежности и найти путь с минимальным числом ребер из вершины v ₁ в вершину v ₇.

4. Определить, содержит ли граф на рис. 13 а эйлеров цикл или эйлерову цепь.

5. Может ли вершина, входящая в цикл графа, иметь степень, меньшую двух?

6. Как называется путь, у которого начало первой дуги совпадает с концом последней?

7. Как называется маршрут, у которого первая вершина совпадает с последней?

8. Показать, что в любом графе количество вершин нечетной степени четно.

9. Показать, что из всякого замкнутого маршрута нечетной длины можно выделить простую цепь.

10. Показать, что ребро, входящее в цикл графа, входит в некоторый его простой цикл.

Для самостоятельной работы

1. Задан граф G (рис. 13 а). Найти путь с минимальным числом ребер из вершины v ₁ в вершину v ₇ графа G.

2. Для графа G (рис. 13 б) записать матрицу смежности и найти путь с минимальным числом ребер из вершины v ₁ в вершину v ₈.

3. Для графа G (рис. 13 б) записать матрицу инцидентности.

4. Для орграфа D (рис. 13 в) записать матрицу смежности и найти путь с минимальным числом ребер из вершины v ₁ в вершину v ₆.

5. Показать, что любая вершина, входящая в цикл, не является висячей.

6. Доказать, что если в орграфе отсутствуют вершины с нулевой полустепенью исхода (захода), то в орграфе имеется простой контур.

7. Доказать, что удаление из орграфа вершины v с d⁺(v) ≤ 1 (d^-(v) ≤ 1) приводит к орграфу, контуры которого совпадают с контурами исходного орграфа.

8. Привести определение простой цепи:

а) цепь, в которой вершины и ребра повторяются;

б) чередование вершин и ребер;

в) цепь, в которой все вершины попарно различны.

9. В чем заключается понятие смежности?

а) сежными являются вершины, инцидентные одному ребру;

б) смежными являются два ребра, не имеющие общих вершин;

в) смежными являются вершины, соединенные некоторым маршрутом.

10. Задан псевдограф G. Цепь в G называется эйлеровой, если…

а) она проходит по одному разу через каждую точку псевдографа;

б) она проходит по одному разу через каждое ребро псевдографа;

в) она проходит по одному разу через вершины и ребра.

Литература

1. Новиков, Ф. А. Дискретная математика для программистов: учебник для вузов / Ф. А. Новиков. – СПб.: Питер, 2001. – 304 с.

2. Акимов, О. Е. Дискретная математика. Логика, группы, графы. – 2-е изд., доп. / О. Е. Акимов. – М.: Лаборатория базовых знаний, 2001. – 367 с.

Дата добавления: 2017-02-01