Пояснение к работе

Практическое занятие № 4

Тема: «Функции и отображения»

Цель занятия:

усвоение таких понятий, как функция, отображение, область определения и область значений функции, инъекция, сюръекция, биекция.

Время выполнения практического задания – 2 часа.

Последовательность выполнения

1. Руководствуясь приведенным теоретическим материалом, ответить на следующие вопросы:

Как обозначается функция (отображение)?

Что является областью определения функции?

Что является областью значений функции?

Какая функция называется инъективной?

Какая функция называется сюръективной?

Какая функция называется биективной?

В чем заключается понятие однозначности или функциональности?

Чему равна композиция двух функций?

Какое из отношений является функцией:

{<1, 2>, <3, 4>, <4, 4>, <5, 6>}; {<1, 2>, <1, 4>, <4, 4>, <5, 6>}.

2. Дать определение функции.

3. Выполнить задания для аудиторных занятий.

4. Выполнить задания для самостоятельной работы.

4.1. Функции и отображения

Пусть f – отношение на А и В, такое, что "(a, b) Î f и (a, c) Î f Þ b = c. Такое свойство отношений называется однозначностью или функциональностью, а само отношение называется функцией из А в В и обозначается следующим образом: f: A ® B, то есть осуществляется отображение множества А на множество В. Если f: A ® B, то обычно используется префиксная форма записи: b = f(a):= (a, b) Î f. Если b = f(a), то а называют аргументом или прообразом элемента b при функции f, а b – значением функции или образом элемента а при f. Итак, из всех отношений функции выделяются тем, что каждый элемент из области определения имеет единственный образ. Область определения функции: f_A:= { a Î A ç$ b Î B, b =f(a)}; область значений функции: f_В:= { b Î B ç$ a Î A, b = f(a)}.

Функция f называется: инъективной, если b =f(a ₁) и b =f(a ₂) Þ а ₁ = а ₂; сюръективной, если " b Î В $ а Î А b = f(a); биективной, если она инъективна и сюръективна.

Примеры:

1. {<1, 2>, <3, 4>, <4, 4>, <5, 6>} – функция, f_А = {1, 3, 4, 5};

f_В = {2, 4, 6}; {< x, y >: x, y Î R, y = x² } – функция, f_А = f_В = (–¥, ¥);

{<1, 2>, <1, 4>, <4, 4>, <5, 6>} – отношение, но не функция.

2. Даны три функции, отображающие множество действительных чисел R во множество действительных чисел, f_i : R ® R. i = 1, 2, 3:

а) функция f₁(х) = е ^х инъективна, но не сюръективна; б) функция f₂(х) = х ³ – х сюръективна, но не инъективна; в) функция f₃(х) = 2 х + 1 биективна.

Композиция двух функций есть функция. При этом, если f: Х ® У, g: Y ® Z, то gO f: Х ® Z.

Задания

Для аудиторных занятий

1. Привести примеры отображений:

а) R ® R;

б) R ® R ⁺;

в) R ⁺ ® R.

2. Найти f(A), где А = {(х, у)Î R ´ R | у = 2 х + 3 }, для следующих отображений:

а) f: (x, y) ® (y, x);

б) f: (x, y) ® (− y, −x);

в) f: (x, y) ® (x, −y).

3. Для каждого из следующих отображений исследовать, является ли оно инъективным, сюръективным:

а) f: R ® R, х ® x ² + 3 х + 5;

б) f: R ® R, х ® x ² + e^x;

в) f: R ® R, х ® x ⁷ + х + 1.

4. Указать все сюръективные отображения множества А = {1, 2, 3} на множество В ={ а, b }. Существуют ли инъективные отображения А в В?

5. Пусть А и В – конечные множества, | А | = m, | B | = n.

a) сколько существует бинарных отношений между элементами множеств А и В?

б) сколько существует отображений из А в В?

6. Пусть a: х ® х ²; b: х ® х ³ – отображения R ® R. Найти a b и b a.

7. Для каждого из следующих бинарных отношений исследовать, является ли оно всюду определенным и функциональным:

а) {(х, у) Î R ⁺ ´ R | у ² = х };

б) {(х, у) Î[ −1, 1] ´ R | х = sin y };

в) {(х, у) Î N ´ N | x < у ≤ х + 1}.

8. Доказать, что каждое из следующих бинарных отношений является отображением R в R:

а) {(х, у) Î R ´ R | у = х ² − 1};

б) {(х, у) Î R ´ R | у = sin х + 1};

в) {(х, у) Î R ´ R | у = 2 ^х}.

9. Для каждого из следующих бинарных отношений исследовать, является ли оно всюду определенным, функциональным; ответ обосновать.

а)

б)

в)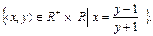

10. Пусть А и В – конечные множества, ½ А ½ = ½ В ½ = n.

а) сколько существует бинарных отношений между элементами множеств А и В?

б) сколько существует отображений А в В?

Для самостоятельной работы

1. Привести примеры отображений:

а) R ® [0, 1];

б) Z ® N;

в) R ® N.

2. Найти f(A), где А = {(х, у)Î R ´ R | у = 2 х + 3}, для следующих отображений:

а) f: (x, y)®(− x, y);

б) f: (x, y)®(у − 2, х + 2).

3. Для каждого из следующих отображений исследовать, является ли оно инъективным, сюръективным:

а) f: R ® R, х ® 2 x ⁵ − 1;

б) f: R ® R, х ® x ² + ;

в) f: R ® R, х ® x ² + ln x.

4. Пусть А и В – конечные множества, | А | = m, | B | = n.

а) при каких m и n существует инъективное отображение А в В?

б) при каких m и n существует биекция А на В?

в) пусть существуют биекции А на А ^’ и В на В ^’. Доказать, что существует биекция А ´ В на А ^’ ´ В ^’.

5. Для каждого из следующих бинарных отношений исследовать, является ли оно всюду определенным и функциональным:

а) {(х, у) Î N ´ N | x / у };

б) {(х, у) Î N ´ N | x = у ²};

в) {(х, у) Î Z ´ Z | у = | х |}.

6. Доказать, что каждое из следующих бинарных отношений является отображением R в R:

а) {(х, у) Î R ´ R | у = х ² − x − 1};

б) {(х, у) Î R ´ R | у = log₂| х |}.

в) {(х, у) Î R ´ R | у = }.

7. Для каждого из следующих бинарных отношений исследовать, является ли оно всюду определенным, функциональным; ответ обосновать.

а) {á х, у ñ Î N ´ N | x < у £ х + 1};

б) {á х, у ñ Î N ´ N | x / у };

в) {á х, у ñ Î N ´ N | x = у ²}.

8. Указать все сюръективные отображения множества А = {1, 2, 3} на множество B = {a, b}. Существуют ли инъективные отображения А в В?

9. Найти все отображения множества А = {1, 2} в себя, укажите, какие из них инъективные, сюръективные.

10. Пусть f – отображение конечного множества А в себя. Докажите, что f инъективно тогда и только тогда, тогда f сюръективно.

Литература

1. Куликов, Л. Я. Сборник задач по алгебре и теории чисел / Л. Я. Куликов, А. И. Москаленко, А. А Фомин. – М.: Просвещение, 1993. – 288 с.

2. Новиков, Ф. А. Дискретная математика для программистов: учебник для вузов / Ф. А. Новиков. – СПб.: Питер, 2001. – 304 с.

Дата добавления: 2017-02-01