
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Пояснение к работе
|
|
|
|
Множествами. Применение диаграмм Эйлера-Венна при
Тема: «Начальные понятия теории множеств. Операции над
Практическое занятие № 1
решении практических задач»
Цель занятия:
познакомить студентов с такими понятиями, как множество, элементы множеств, булеан, универсальное множество, мощность множества, операции над множествами, представления множеств с помощью диаграмм, формируя у них терминологический запас.
Время выполнения практического задания – 4 часа.
Последовательность выполнения
1. Руководствуясь приведенным теоретическим материалом, ответить на следующие вопросы:
Как обозначаются множества и элементы множеств?
Какое множество называется конечным?
Какие существуют способы задания множеств?
Как определяется мощность множества?
2. Дать определение следующих понятий:
– множество и элементы множества;
– операции разности и объединения множеств;
– операции пересечения и дополнения;
– универсальное множество и булеан.
3. Перечислить основные тождества алгебры множеств.
4. Представить операции над множествами в виде диаграмм.
5. Выполнить задания для аудиторных занятий.
6. Выполнить задания для самостоятельной работы.
1.1. Начальные понятия теории множеств
Любое понятие дискретной математики можно определить с помощью понятия множества. Под множеством понимают объединение в одно общее объектов, хорошо различаемых нашей интуицией или нашей мыслью. Объекты, которые образуют множество, будем называть элементами множества и обозначать малыми буквами латинского алфавита.
Множество и его элементы обозначаются следующим образом:
А = { a1, a2, a3 } – множество, состоящее из трех элементов;
А = { a1, a2, … } – множество, состоящее из бесконечного числа элементов. Множество может состоять из элементов, которые сами являются множествами. Нужно различать элемент a и множество, состоящее из единственного элемента a.
Пример. Множество А = {1, 2} состоит из двух элементов 1, 2; но множество { А } состоит из одного элемента А.
Если элемент a принадлежит множеству А, это записывается следующим образом: a Î А. Если элемент a непринадлежит множеству А, то записывают так: a Ï А. Если какое-либо множество А включено в другое множество В, то используется запись А Ì В. Множество, содержащее конечное число элементов, называется конечным, если множество не содержит ни одного элемента, то оно называется пустым и обозначается Æ. Принято считать, что пустое множество является подмножеством любого множества: Æ Í А, где А – любое множество. Таким образом, всякое множество содержит в качестве своих подмножеств пустое множество и само себя.
Пример. 1. Множество корней уравнения sin x = 2 является пустым.
2.Пусть А1 – множество простых чисел, А 2 – множество целых чисел, a = 4. Тогда a Î А 2, a Ï А 1.
Множество считается заданным, если каким-либо образом указано некоторое свойство, которым обладают все его элементы и не обладают никакие другие объекты.
Множество может быть задано различными способами: перечислением элементов (конечные множества) или указанием их свойств (при этом в обоих случаях при задании множеств используют фигурные скобки).
Примеры задания множеств. 1. Множество M цифр десятичного алфавита можно задать в виде: M = {0, 1,..., 9} или M = { х │ х – целое, 0 £ х £ 9}, где справа от вертикальной черты указывают свойство элементов этого множества. Множество M чётных чисел можно записать в виде: M = { х│х – чётное число}.
2. Если R – множество точек числовой прямой, то Rn – множество точек n -мерного арифметического пространства; в частности, R2 – множество точек плоскости, R3 – множество точек пространства трех измерений.
Для каждого множества М существует множество, элементами которого являются подмножества множества М и только они. Такое множество будем называть семейством множества М или булеаном этого множества и обозначать В(М), а множество М будем называть универсальным (универсумом или пространством) и обозначать 1 или U. Множество М (универсальное) не должно быть ýже объединения рассматриваемых множеств, т. е. оно должно быть равно или содержать объединение рассматриваемых множеств.
Пример. Пусть множество А = {1, 2} состоит из двух элементов 1, 2. Тогда множество В(A) включает в себя пустое множество Æ, два одноэлементных множества {1} и {2} и само множество А = {1, 2}, т. е.
В(A) = {Æ, {1}, {2}, {1, 2}}. Мы видим, что множество В(A) состоит из четырех элементов (4 = 22).
Приведем стандартные обозначения для некоторых наиболее употребительных числовых множеств:
N – множество натуральных чисел (иногда его начинают с 1, иногда с 0; обычно это оговаривается);
Р – простые числа;
Z – множество целых чисел (положительные, отрицательные и 0);
R – множество действительных чисел.
Очевидное соотношение: N Í Z Í R.
Рассмотрим методы получения новых множеств из уже существующих на примере пространства или множества U, определив в нём 4 операции над множествами A и B: объединение, пересечение, разность, дополнение.
1.2. Операции над множествами
Объединением А и В называется множество А È В, все элементы которого являются элементами хотя бы одного из множеств А или В:
А È В = { x ç x Î А и / или x Î В }.
Из определения следует, что А Í А È В и В Í А È В. Аналогично определяется объединение нескольких множеств.
Пример. 1. Пусть А = {4, 5, 6}, В = {2, 4, 6}. Тогда А È В = {2, 4, 5, 6}.
2. Пусть А – множество чисел, которые делятся на 2, а В – множество чисел, которые делятся на 3: А = {2, 4, 6, …}, В = {3, 6, 9, …}. Тогда А È В – множество чисел, которые делятся на 2 или на 3: А È В = {2, 3, 4, 6, 8, 9, 10, …}.
Пересечением множеств А и В называется множество А Ç В, все элементы которого являются элементами обоих множеств А и В: А Ç В = { x ç x Î А и x Î В }. Из определения следует, что А Ç В Í А, А Ç В Í В и А Ç В Í А È В. Аналогично определяется пересечение нескольких множеств.
Пример. 1. Пусть А = {4, 5, 6}, В = {2, 4, 6}. Тогда А Ç В = {4, 6}.
2. Пусть А – множество чисел, которые делятся на 2, а В – множество чисел, которые делятся на 3: А = {2, 4, 6, …}, В = {3, 6, 9, …}. Тогда А Ç В – множество чисел, которые делятся и на 2, и на 3: А È В = {6, 12, 18, …}.
Может оказаться, что множества не имеют ни одного общего элемента. Тогда говорят, что множества не пересекаются или что их пересечение – пустое множество.
Пример. Пусть А = {1, 2}, В = {2, 3}, C = {3, 4}. Тогда А Ç В Ç C = Æ.
Разностью (относительным дополнением) множества В до множества А называется множество А \ В, все элементы которого являются элементами множества А, но не являются элементами множества В:
А \ В = { x ç x Î А и x Ï В }.
Пример. 1. А = {4, 5, 6}, В = {2, 4, 6}. А \ В = {5}, В \ А = {2}.
2. А = {2, 4, 6, …}, В = {3, 6, 9, …}. Тогда А \ В –множество чисел, которые делятся на 2, но не делятся на 3, а В \ А – множество чисел, которые делятся на 3, но не делятся на 2: А \ В = {2, 4, 8, 10, 14, …}. В \ А = {3, 9, 15, 21, 27, …}.
Симметрической разностью множеств А и В называется множество А + В: А + В = (А \ В) È (В \ А).
Пример. 1. А = {4, 5, 6}, В = {2, 4, 6}. А \ В = {5}, В \ А = {2}, А + В = {2, 5}.
2. А = {2, 4, 6, …}, В = {3, 6, 9, …}, А \ В = {2, 4, 8, 10, 14, …}.
В \ А = {3, 9, 15, 21, 27, …}, А + В = {2, 3, 4, 8, 9, …}.
Дополнением ` М множества М является множество
` М = { mi │ mi Ï M }.
Пример. Заданы множества А = {1, 2, 5, 6} и В = {2, 3, 4, 6} на универсальном множестве U = {1, 2, 3, 5, 6, 7}. Выполнить операции` А,`В.
Решение. В результате выполнения заданных операций получим следующие множества: ` А = {3, 7};` В = {1, 5, 7}.
Для конечных множеств существует понятие: мощность множества А – число его элементов. Обозначают мощность множества | А |.
Пример. А = {1, 2, 5, 6}, тогда мощность множества | А | = n(А) = 4; |Æ| = 0; |{Æ}| = 1.
Также справедливы следующие формулы: для любых множеств А и В Þ | А È В | = | А | + | В | – | А Ç В |, то есть учитываются общие для обоих множеств элементы.
Пример. А = {1, 2, 3} | А | = 3; В = {1, 2, 3, 4, 5} | В | = 5, тогда А È В = {1, 2, 3, 4, 5} | А È В | = 5; А Ç В = {1, 2, 3} | А Ç В | = 3, то есть получим равенство: | А È В | = | А | + | В | – | А Ç В | 5 = 3 + 5 – 3.
Для конечного множества М мощность его булеана | В(М) | равна 2|М|.
1.3. Применение диаграмм Эйлера-Венна при решении практических задач
Для наглядного представления множеств и отношений между ними используются диаграммы Эйлера-Венна. Универсальное множество изображают в виде прямоугольника, а множества, входящие в универсальное множество, в виде кругов внутри прямоугольника; элементу множества соответствует точка внутри круга (рис. 1).
С помощью диаграмм Эйлера-Венна удобно иллюстрировать операции над множествами. Результирующее множество каждой операции выделено штриховкой.

| 
| 
|
| MA | MAÈMB | MAÇMB |

| 
| 
|
| MB\MA | MA\MB | `МA |
Рис. 1. Представление операций над множествами с помощью диаграмм Эйлера-Венна
Пример. Рассмотрим операцию дополнения множества, являющегося пересечением множеств MА и MВ. Необходимо доказать, что её результат совпадает с объединением дополнений этих множеств:
Решение. M = 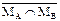 =` MА È` MВ.
=` MА È` MВ.
В этом можно убедиться с помощью диаграмм Эйлера-Венна (рис. 2).
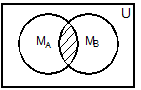
| 
| |
| MA Ç MB | 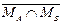
| |

| 
| 
|
| ` МA | ` МB | ` MА È` MВ |
Рис. 2
Для любых подмножеств А, В и С универсального множества U выполняются следующие тождества (основные тождества алгебры множеств):
| 1. А È В = В È А (коммутативность È). | 1¢. А Ç В = В Ç А (коммутативность Ç). |
| 2. А È (В È С) = (А È В) È С (ассоциативность È). | 2¢. А Ç (В Ç С) = (А Ç В) Ç С (ассоциативность Ç). |
| 3. А È (В Ç С) = (А È В) Ç (А È С) (дистрибутивность È относительно Ç). | 3¢. А Ç (В È С) = (А Ç В) È (А Ç С) (дистрибутивность Ç относительно È). |
| 4. А È Æ = А (свойство нуля). | 4¢. А Ç Æ = Æ. |
| 5. А È` А = U (свойство дополнения). | 5¢. А Ç` А = Æ. |
| 6. А È А = А. | 6¢. А Ç А = А. |
| 7. А È U = U (свойство единицы). | 7¢. А Ç U = А. |
8.  =` А Ç` В (закон де Моргана). =` А Ç` В (закон де Моргана).
| 8¢.  =` А È` В (закон де Моргана). =` А È` В (закон де Моргана).
|
| 9. А È (А Ç В) = А (закон поглощения). | 9¢. А Ç (А È В) = А (закон поглощения). |
10. 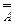 = А (инволюция). = А (инволюция).
| |
11. А \ В = А Ç 
|
Примеры. 1. Рассмотрим предположение о том, что произвольные множества A и B попарно эквивалентны: 1) A Ì B; 2) A Ç B = A; 3) A È B = B.
Решение. Докажем, что из первого предположения следует второе. Действительно, так как A Ç B Ì A, то достаточно показать, что в этом случае A Ì A Ç B. Но если х Î A, то х Î B, т. к. A Ì B и, следовательно, х Î A Ç B.
Докажем, что из второго предположения следует третье. Так как A Ç B = A, то A È B = (A Ç B) È B. По закону поглощения (см. тождество 9) B È (A Ç B) = B. Отсюда, используя закон коммутативности, получаем A È B = B.
Докажем, что из третьего предположения следует первое. Так как A Ì A È B, а по условию третьего предположения A È B = B, то А Ì В.
Задания
Для аудиторных занятий
1.Записать множество М целых чисел х, которые делятся на три и находятся в интервале 3 £ х £ 15. Записать двумя способами.
2.Записать множество А целых чисел х, которые делятся на 2 и на 3 и находятся в интервале 20 £ х £ 25. Записать двумя способами.
3.Принадлежит ли х множеству М, если:
а) М = {2, 6, 8, …, 50}; х = 35;
б) М = {2, 3, 4, 6, 8, 9, 10, …, 100}; х = 23;
в) М = {-2, 2, -4, 4, …, 120}; х = -30.
Записать приведенные множества с указанием свойств их элементов.
4.Доказать неравенство: {{1, 2}, { 2, 3}} ¹ {1, 2, 3}.
5.Какие из следующих выражений являются истинными и какие ложными:
а) Æ Î {{Æ}}; б) 1 Î {{1, 2}}; в) {1, 2} Î {{1, 2}}; г) {1, 2} Î {{1, 2}, {1, 3}, 1, 2}.
6. Привести примеры таких множеств А, В, С, чтобы были истинными следующие высказывания:
а) А Î В Ù В Î С Ù А Ï С;
б) А Î В Ù В Î С Ù А Î С.
7. Какие из следующих множеств конечны и какие бесконечны:
а) { x Î R ç x 2 - 5 x + 4 = 0};
б) { x Î N ç x 2 - 5 x + 4 > 0};
в) { x Î N ç x 2 / 24}.
8. Равны ли множества:
а) { x Î R ç x 2 - 2 x – 2 = 0} и { x Î Q ç x 2 - 2 x – 2 = 0};
б) { x Î Z ç4/ x Ù 15/ x } и { x Î Z ç4/ x Ù 15/ x }{ x Î Z ç20/ x Ù 30/ x }.
9. Перечислить элементы следующих множеств:
а) { x Î R ç x 2 - 3 x + 2 = 0};
б) { x Î R ç x 2 + 1 = 0};
в) множество всех корней уравнения x 2 + 6 x + 9 = 0.
10. Перечислить все элементы каждого из следующих множеств:
а) { x ç x Í{ 1}}; в) { x ç x Í {1, 2, 3}};
б) { x ç x Í {1, 2}}; г) { x ç x Í Æ}.
Для самостоятельной работы
1. Перечислить элементы следующих множеств:
а) множество четных чисел от 0 до 20 включительно;
б) множество всех двузначных чисел, делящихся на 5 и не делящихся на 10;
в) множество всех последовательностей, содержащих все числа 1, 2, 3, 4, 5 и только эти числа, в которых четные и нечетные числа чередуются.
2. Равны ли множества:
а) {2, 4, 5} и {2, 4, 2, 5}; б) {1, 2} и {{1, 2}}; в) {1, 2, 3} и {3, 1, 2, 1}};
г) {1, 2, 3} и {{1}, {2},{3}}.
3. Перечислить подмножества следующих множеств:
а) {{1, 2}, {3}, 4}; б) {{5, 2}}; в) {{2}, {6}, {3} }; г) {{4, 6}, {1}, 1}.
4. Вставить между множествами символ Î или Ì так, чтобы получилось истинное высказывание:
а) {1} {1, {1, 2}}; б) Æ {Æ}; в) Æ {{Æ}}; г) {1, 2} {1, 2, {1, 2}}.
5. Найти А È В, А Ç В, А \ В, В \ А,` А,` В:
а) А = {1, 2, 3}, В = {2, 3, 5, 4}, U = {1, 2, …, 9};
б) А = { х ׀ х делится на 2}, В = { х ׀ х делится на 3}, U = N.
6. Доказать следующие тождества:
| а) (А Ç В) È (А Ç` В) = (А È В) Ç (А È` В); | е) А Ç В = А Ç (А È В); |
| б) (А È В) Ç А = А Ç В; | ж) (А È В) \ (А Ç В) = (А \ В) È (В \ А); |
| в) (А \ В) \ С = (А \ С) \(В \ С); | з) (А \ В) È (А \` В) = (А È В) \ (А Ç В); |
| г) А \ (В È С) = (А \ В) \ С; | и) (А \` В) È (В \` А) = (А È В) \ (А Ç В); |
| д) А \ В = А Ç` В; | к) А \ (В È С) = (А \ В) Ç (А \ С). |
7. Показать с помощью диаграмм Эйлера-Венна, какие из следующих утверждений верны:
| а) (А È В) Ç С = А È (В Ç С); | в) (А \ В) È С = (А È С) \ (В È С); |
| б) (А \ В) È В = А; | г) (А Ç` В) È (В Ç` А) Ì В. |
8. Найти мощность множеств, мощность их булеанов и | А È В | – мощность объединения множеств:
а) А = {4, 5, 6}, В = {4, 5, 6, 7, 8}; б) А = {1, 3, 5, 6}, В = {4, 5, 6, 7};
в) А = {3, 5, 7}, В = {2, 5, 6, 7, 9}; г) А = {1, 2, 3, 5}, В = {2, 4, 5, 6, 7}.
9. Вставить между множествами символ Î или Í так, чтобы получилось истинное высказывание:
а) {1} {1, {1, 2}}; г) Æ {1, 2, {1}, {Æ}};
б) {1, 2} {1, 2, {1},{2}}; д) Æ {{Æ}};
в) {1, 2} {1, 2,{1, 2}}; е) Æ {Æ}.
10. Привести пример множеств A, B, C, таких, чтобы выполнялись условия:
а) A Î B, B Ï C, A Í C;
б) A Î B, A Ï C, C Í B;
в) A Í B, B Î C, A Ï C.
Литература
1. Куликов, Л. Я. Сборник задач по алгебре и теории чисел / Л. Я. Куликов, А. И. Москаленко, А. А Фомин. – М.: Просвещение, 1993. – 288 с.
2. Ерусалимский, Я. М. Дискретная математика. Теория, задачи, приложения: учеб. пособие для вузов / Я. М. Ерусалимский. – М.: Вузовская книга, 2008. – 288 с.
3. Новиков, Ф. А. Дискретная математика для программистов: учебник для вузов / Ф. А. Новиков. – СПб.: Питер, 2001. – 304 с.
|
|
|
|
|
Дата добавления: 2017-02-01; Просмотров: 313; Нарушение авторских прав?; Мы поможем в написании вашей работы!