Пояснение к работе

Практическое занятие № 7

Тема: «Связность, компоненты связности»

Цель занятия:

усвоение таких понятий, как связность, компоненты связности, односторонняя связность, сильная связность, матрица связности.

Время выполнения практического задания – 2 часа.

Последовательность выполнения

1. Руководствуясь приведенным теоретическим материалом, ответить на следующие вопросы:

Когда одна вершина достижима из другой?

Какой граф называется связным?

Какой граф называется сильно связным?

Какой граф называется односторонне связным?

Какой псевдограф называется ассоциированным с ориентированным псевдографом?

Какой граф называется слабо связным?

Что называется компонентой связности графа G (орграфа D)?

Что называется компонентой сильной связности графа G (орграфа D)?

Что понимают под операцией удаления вершины из графа (орграфа)?

Какая вершина графа называется разделяющей или точкой сочленения?

2. Выполнить задания для аудиторных занятий.

3. Выполнить задания для самостоятельной работы.

7.1. Связность, компоненты связности

Говорят, что вершина w орграфа D (графа G) достижима из вершины v, если существует путь из v в w (маршрут, соединяющий v, w).

Граф (орграф) называется связным (сильно связным), если для любых двух его вершин v, w существует маршрут (путь), соединяющий v, w (из v в w). Орграф называется односторонне связным, если для любых двух его вершин, по крайней мере одна достижима из другой.

Псевдографом ассоциированным с ориентированным псевдографом D = (V, E), называется псевдограф G = (V, E ₀), в котором E ₀ получается из Е заменой всех упорядоченных пар (v, w) на неупорядоченные { v, w } (рис. 14).

а б Рис. 14: а – ориентированный псевдограф, б – ассоциированный с ним псевдограф

Орграф называется слабо связным, если связным является ассоциированный с ним псевдограф. Если граф (орграф) не является связным (слабо связным), то он называется несвязным.

Компонентой связности (сильной связности) графа G (орграфа D) называется его связный (сильно связный) подграф, не являющийся собственным подграфом никакого другого связного (сильно связного) подграфа графа G (орграфа D).

Примеры: 1. У графа, изображенного на рис. 15, три компоненты связности.

2. У графа, изображенного на рис. 16, три компоненты сильной связности, показанные на рис. 17 а, 17 б.

а б

Рис. 15 Рис. 16 Рис. 17

3. На рис. 18 показаны диаграммы сильно, односторонне и слабо связных графов.

Рис. 18

Утверждение 1. Пусть G = (V, E) – псевдограф с p компонентами связности: G ₁ = (V ₁, E ₁), …, Gp = (Vp, Ep), тогда

1) V = V ₁È … È Vp, E = E ₁È … È Ep, то есть G = G ₁ È … È Gp;

2) Vi Ç Vj = Æ, Ei Ç Ej = Æ при i ¹ j.

Утверждение 2. Пусть D = (V, E) – ориентированный псевдограф с p компонентами сильной связности: D ₁ = (V ₁, E ₁), …, Dp = (Vp, Ep), тогда

1) V = V ₁È … È Vp, E = E ₁È … È Ep, то есть D = D ₁È … È Dp;

2) Vi Ç Vj = Æ, Ei Ç Ej = Æ при i ¹ j.

Утверждение 3. Пусть r – отношение достижимости на множестве V вершин псевдографа G, то есть vrw тогда и только тогда, когда либо v = w, либо существует маршрут, соединяющий v, w, тогда:

1) r – эквивалентность на V;

2) vrw тогда и только тогда, когда вершины v, w принадлежат одной компоненте связности псевдографа G;

3) для любого класса эквивалентности Vi Î V / r псевдограф Gi, порожденный множеством Vi, является компонентой связности псевдографа G;

4) для любой компоненты связности псевдографа Gi = (Vi, Еi) псевдографа G выполняется Vi Î V / r.

Утверждение 4. Пусть r ₁ – отношение достижимости на множестве V вершин ориентированного псевдографа D, то есть vr ₁ w тогда и только тогда, когда вершина w достижима из вершины v. Пусть r₂ – отношение двусторонней достижимости на множестве V, то есть r ₂ = r ₁ ∩ r ₁^-1, тогда:

1) r ₁ рефлексивно, транзитивно;

2) r ₂ – эквивалентность на V;

3) vr ₂ w только тогда, когда вершины v, w принадлежат одной компоненте сильной связности ориентированного псевдографа D;

4) для любого класса эквивалентности Vi Î V / r ₂ ориентированный псевдограф Di, порожденный множеством Vi, является компонентой сильной связности ориентированного псевдографа D;

5) для любой компоненты сильной связности Di = (Vi, Еi) ориентированного псевдографа D выполняется Vi Î V / r ₂.

Под операцией удаления вершины из графа (орграфа) понимают операцию, заключающуюся в удалении некоторой вершины вместе с инцидентными ей ребрами (дугами).

Вершина графа, удаление которой увеличивает число компонент связности, называется разделяющей или точкой сочленения.

7.2. Матрица связности

Пусть D = (V, E) – орграф, где V = { v ₁, …, v_n }. Матрицей достижимости орграфа D называется квадратная матрица Т(D) = [ t_i,j ] порядка n, у которой t_i,j =1, если вершина vj достижима из vi и t_i,j = 0 – в противном случае. Матрицей сильной связности орграфа D называется квадратная матрица S(D) = [ s_i,j ] порядка n, у которой s_i,j =1, если вершина vi достижима из vj и одновременно вершина vj достижима из vi и s_i,j = 0 – в противном случае, то есть s_i,j = 1 тогда и только тогда, когда вершины vi, vj принадлежат одной компоненте сильной связности орграфа D.

Пусть G = (V, E) – орграф, где V = { v ₁, …, v_n }. Матрицей связности графа G называется квадратная матрица S(D) = [ s_i,j ] порядка n, у которой s_i,j = 1, если i = j или существует маршрут, соединяющий вершину vi, vj и s_i,j = 0 – в противном случае (то есть s_i,j = 1 тогда и только тогда, когда вершины vi, vj принадлежат одной компоненте связности орграфа G).

Задания

Для аудиторных занятий

1. Для графов, изображенных на рис. 4, записать последовательности, состоящие из вершин и ребер, являющиеся маршрутами длины 5, 4, 3 и 2 соответственно.

2. Для графов, изображенных на рис. 9 а, 9 б, 9 в, записать последовательности, состоящие из вершин и ребер, являющиеся цепью, простой цепью.

3. Для графов, изображенных на рис. 9 а, 9 б, 9 в, записать последовательности, состоящие из вершин и ребер, являющиеся циклом, контуром.

4. Для орграфа D, представленногона рис. 19, записать матрицу достижимости и матрицу сильной связности.

Рис. 19 Рис. 20

5. Для графа G (рис. 20) записать матрицу связности.

6. Можно ли утверждать, что сильно связный граф всегда содержит контур?

7. Сколько компонент связности содержит граф G (рис. 20)?

8. Какие вершины графа (рис. 21) являются точками сочленения?

Рис. 21

9. Задано отношение достижимости r на множестве V. Какими свойствами обладает отношение r (рефлексивность, симметричность, транзитивность)?

10. Доказать, что в связном графе, содержащем по крайней мере две вершины, найдется вершина, не являющаяся точкой сочленения.

Для самостоятельной работы

1. Сколько компонент связности содержит граф D (рис. 19)?

2. Какие вершины графа (рис. 20) являются точками сочленения?

3. Сколько компонент связности содержит граф G (рис. 21)?

4. Для графа G, изображенного на рис. 21, записать матрицу связности.

5. Какие из следующих графов являются полно связными (рис. 22)?

а) б) в)

Рис. 22

6. Сколько компонент связности у заданного графа?

7. Определить матрицы достижимости для орграфов с матрицами смежности.

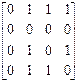
8. Определить матрицы сильной связности для орграфов с матрицами смежности.

9. Сколько компонент связности у орграфов из заданий 7 и 8?

10. Какими свойствами обладают графы из заданий 7 и 8 (рефлексивность, симметричность, транзитивность)?

Литература

1. Новиков, Ф. А. Дискретная математика для программистов: учебник для вузов / Ф. А. Новиков. – СПб.: Питер, 2001. – 304 с.

2. Акимов, О. Е. Дискретная математика. Логика, группы, графы – 2-е изд., доп. / О. Е. Акимов. – М.: Лаборатория базовых знаний, 2001. – 367 с.

3. Гаврилов, Г. П. Задачи и упражнения по курсу дискретной математики: учеб. пособие / Г. П. Гаврилов, А. А. Сапоженко. – М.: Наука, 1992. – 408 с.

Дата добавления: 2017-02-01