Пояснение к работе

Практическое занятие № 10

Тема: «Переключательные (булевы) функции»

Цель занятия:

усвоение таких понятий, как булевы функции, формулы логики булевых функций, булева алгебра, замкнутые классы.

Время выполнения практического задания – 4 часа.

Последовательность выполнения

1. Руководствуясь приведенным теоретическим материалом, ответить на следующие вопросы:

Как реализуется табличное представление булевой функции?

Что является важнейшей интерпретацией теории булевых функций?

Какие существуют элементарные булевы функции двух переменных?

Как задается функция вектором ее значений?

Какие булевы функции называются равными?

Какая система булевых функций называется полной?

2. Дать определение следующих понятий:

– булева функция;

– фиктивная и существенная переменная;

– булева алгебра (алгебра логики).

3. Записать булеву функцию в виде произвольного отображения.

4. Выполнить задания для аудиторных занятий.

5. Выполнить задания для самостоятельной работы.

10.1. Основные определения

Булевой функцией f (x ₁, x ₂,..., x_n) называется произвольная функция n переменных, аргументы которой x ₁, x ₂,..., x_n и сама функция f принимают значения 0 или 1, т. е. x_i {0, 1}, i = 1, 2,..., n; f (x ₁, x ₂,..., x_n) {0, 1}. Булева функция от n переменных – это произвольное отображение вида f: {0, 1}ⁿ → {0, 1}.

Одной из важнейших интерпретаций теории булевых функций является теория переключательных функций. Первоначально математический аппарат теории булевых функций был применен для анализа и синтеза релейно-контактных схем с операциями последовательного и параллельного соединения контактов.

Любая булева функция может быть представлена таблицей, в левой части которой перечислены все наборы переменных (2 ⁿ), а в правой части – значения функции. Для формирования столбца значений переменных удобен лексикографический порядок, в соответствии с которым каждый последующий набор значений получается из предыдущего прибавлением 1 в двоичной системе счисления.

Функций одной переменной четыре. Из них выделим функцию “отрицание x ” (обозначается Ø x). Булевых функций двух переменных – 16. Те из них, которые имеют специальные названия (элементарные функции), представлены в табл. 2.

Таблица 2

x 1 x 2	x 1V x 2	x 1& x 2; x 1Ù x 2	x 1 x 2; x 1→ x 2	x 1~ x 2	x 1 Å x 2	x 1¯ x 2	x 1ï x 2
0 0 0 1 1 0 1 1		0	1	1
Названия	дизъ- юнкция	конъюнк-ция	имплика-ция	эквива-лентность	сложение по модулю 2	стрелка Пирса	штрих Шеффера

Остальные функции специальных названий не имеют и могут быть выражены через перечисленные выше функции.

10.2. Формулы логики булевых функций

Формула логики булевых функций определяется индуктивно следующим образом:

1. Любая переменная, а также константы 0 и 1 есть формула.

2. Если A и B – формулы, то A, A Ú B, A & B, A B, A ~ B есть формулы.

3. Ничто, кроме указанного в пунктах 1–2, не есть формула.

Пример. Построим таблицу значений функции f (x ₁, x ₂, x ₃) = Ø(x ₂ Ø x ₃) ~ (Ø x ₁Ú x ₂). Табл. 3 представляет последовательное вычисление этой функции.

Таблица 3

x 1 x 2 x 3	x 3	x 2 x 3	(x 2 x 3)	x 1	x 1V x 2	f (x 1, x 2, x 3)
0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1

Формула так же, как и таблица, может служить способом задания функции. Этот способ аналогичен аналитическому способу задания функций действительной переменной. При этом применяются следующие соглашения:

а) вначале выполняются операции в скобках (внешние скобки у формул опускаются);

б) считается, что связка Ø сильнее любой двухместной связки;

в) связка & сильнее любой другой двухместной связки.

Кроме того, имея в виду стандартное расположение наборов, булеву функцию f() удобно задавать вектором ее значений: 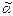_f = (α₀, α₁, …, ), где координата α _i равна значению функции f() на наборе , имеющем номер i (i = 0, 1, …, 2 ⁿ – 1).

10.3. Фиктивные и существенные переменные

Фиктивные переменные. Переменная x _i (1 £ i £ n) функции f(x ₁, …, x_n) называется фиктивной переменной, если значение функции не зависит от значения этой переменной, т. е. для любых значений переменных x₁, …, x _i-1, x _i+1,..., x _n

f(x ₁, …, x _i-1, 0, x _i+1, …, x _n) = f(x ₁, …, x _i-1, 1, x _i+1, …, x _n).

Переменная x _i (1£ i £ n) функции f(x ₁, …, x _n) называется существенной переменной, если можно указать наборы 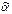и , соседние по i -ой компоненте, что f(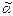) ¹ f(), т. е. f(a ₁, …, a _i-1, 0, a _i+1, …, a _n) ¹ f(a ₁, …, a _i-1, 1, a _i+1, …, a _n).

Булевы функции f и g называются равными, если их существенные переменные соответственно равны и на каждом наборе значений этих переменных функции f и g принимают равные значения.

Замечание: при решении практических задач иногда вместо удаления фиктивных переменных в одной из функций, наоборот, добавляют фиктивные переменные к множеству переменных другой функции.

Пример. Функции f1 = x Å y, f2 = x y Å z, f3 = x Å y Å z Å 1, f4 = xy Å yz Å zx, реализованные формулами, задать векторами своих значений.

Решение. 1. Составим вначале таблицу истинности для f1, f2, f3, f4 (табл. 4).

Таблица 4

(x, y, z)	f1	f3	Xy	f2	yz	zx	f4

2. Тогда функции f1, f2, f3, f4 задаются следующими векторами своих значений: f1() = (0, 0, 1, 1, 1, 1, 0, 0); f2() = (0, 1, 0, 1, 0, 1, 1, 0);

f3() = (1, 0, 0, 1, 0, 1, 1, 0); f4() = (0, 0, 0, 1, 0, 1, 1, 1).

3. f₂ ¹ f₄, т. к. (0, 1, 0, 1, 0, 1, 1, 0) ¹ (0, 0, 0, 1, 0, 1, 1, 1) (в таблице не совпадают значения в столбцах, соответствующих этим функциям).

4. Выписываем f(0, 0, 0) = f(0, 1, 1) = f(1, 0, 1) = f(1, 1, 0) = 1 и

f(0, 0, 1) = f(0, 1, 0) = f(1, 0, 0) = f(1, 1, 1) = 0. Определим, какой переменной является x. Сравнивая значения функции на всех парах наборов, соседних по переменной x, видим, что f(0, y, z)¹ f(1, y, z), x – существенная переменная. Аналогично устанавливаем, что у и z являются существенными переменными.

10.4. Полные системы булевых функций

Как известно, алгеброй называют систему, включающую в себя некоторое непустое множество объектов с заданными на нем функциями (операциями), результатами применения которых к объектам данного множества являются объекты того же множества.

Булевой алгеброй илиалгеброй логики называется двухэлементное множество B = {0, 1} вместе с операциями конъюнкции, дизъюнкции и отрицания.

Система булевых функций { f ₁, f ₂, …, f_n } называется полной, если любая булева функция может быть выражена в виде суперпозиции этих функций. Все логические операции могут быть выражены через операции конъюнкции, дизъюнкции и отрицания. Поэтому система функций {Ø, &, Ú} является полной. Также полными являются следующие системы функций: а) {Ø, Ú}; б) {Ø, &}; в) {Ø, É}.

Полнота систем {Ø, Ú} и {Ø, &} следует из полноты системы {Ø, &, Ú}, а также законов де Моргана и двойного отрицания, следствием которых является возможность выразить конъюнкцию через дизъюнкцию и наоборот: A & B ºØ(Ø A Ú Ø B); A Ú B º Ø(Ø A & Ø B). Поэтому система {Ø, &, Ú} может быть сокращена на одну функцию.

Полнота системы {Ø, É} следует из полноты системы {Ø, Ú} и равносильности, позволяющей выразить импликацию через отрицание и дизъюнкцию: A É B ºØ A Ú B.

Пусть дан класс функций B (т. е. конечное или бесконечное множество функций), объединенных по общему признаку. Замыканием этого класса (обозначение – [B]) будем называть множество всех суперпозиций функций из класса B. Класс B будем называть замкнутым, если его замыкание совпадает с ним самим B = [B].

Рассмотрим классы функций, которые являются замкнутыми.

Класс Т₀ – класс функций, сохраняющих константу 0. f() Î Т₀ Û f(0, …, 0) = 0.

Класс Т₁ – класс функций, сохраняющих константу 1. f(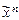) Î Т₁ Û f(1, …, 1) = 1.

Класс S – класс самодвойственных функций. f(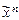) Î S Û f(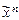) = f*().

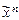Функция называется двойственной к f(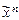), обозначается f*(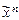), т. е. f *() = .

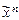Класс М – класс монотонных функций. f(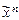) Î М Û " a, b Î , таких, что a £ b Þ f(a) £ f(b).

На множестве наборов значений переменных введем отношение порядка £, называемое отношением предшествования (отношением сравнимости), следующим образом: a £ b, если ai £ bi, i = .

Класс L – класс линейных функций.

f(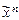) Î L Û f(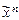) = – представима полиномом Жегалкина не выше первой степени.

Теорема Поста. Система функций полна тогда и только тогда, когда она не находится ни в одном из пяти важнейших замкнутых классов, а именно S, M, L, T₀, T₁.

Пример. Исследовать полноту системы А = {f₁ = x Å y, f₂ = xy Å z, f₃ = x Å y Å z Å 1, f₄ = xy Å yz Å zx }(табл. 4).

Решение. Результаты исследования на принадлежность функций каждому из пяти классов отображены в критериальной таблице (табл. 5).

Таблица 5

	Т0	Т1	L	S	M
f1	+	–	+	–	–
f2	+	–	–	–	–
f3	–	–	+	+	–
f4	+	+	–	+	+

а) f₁, f₂, f₄ Î Т₀, т. к. f₁(0, 0) = 0 Å 0 = 0, f₂(0, 0) = 0 Ù 0 Å 0 = 0, f₄(0, 0, 0) = 0 Ù 0 Å 0 Ù 0 Å 0 Ù 0 = 0; f₃ Ï Т₀, т. к. f₃(0, 0, 0) = 0 Å 0 Å 0 Å 1 = 1;

б) f₁, f₂, f₃ÏТ₁, т. к. f₁(1,1) = 1Å1= 0, f₂(1,1) = 1Ù1Å1 = 0, f₃(1, 1,1) = 1 Å 1 Å 1 Å 1 = 0; f₄ ÎТ1, т. к. f₄(1, 1, 1) = 1 Ù 1 Å 1 Ù 1 Å 1 Ù 1 = 1;

в) f₁, f₃ Î L, т. к. f₁ = x Å y, f₃ = x Å y Å z Å 1 – представимы полиномом Жегалкина первой степени; f₂, f₄ Ï L, т. к. f₂ = xy Å z, f₄ = xy Å yz Å zx – представимы полиномом Жегалкина второй степени;

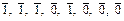г) f₃, f₄ Î S, т. к. f₃*() = () = (1, 0, 0, 1, 0, 1, 1, 0) = f₃(), f₄*() = () = (0, 0, 0, 1, 0, 1, 1, 1) = f₄();

f₁, f₂ Ï S, т. к. f₁*() = = (1, 1, 0, 0, 0, 0, 1, 1) ¹ f₁(),

f₂*() = () = (1, 0, 0, 1, 0, 1, 0, 1) ¹ f₂();

д) f₁, f₂, f₃ Ï М, т. к. f₁: (0, 0, 1, 1) (1, 1, 0, 0), f₂: (0, 1, 0, 1) (0, 1, 1, 0), f₃: (1, 0, 0, 1) (0, 1, 1, 0); f₄ Î М, т. к. f₄: (0, 0, 0, 1) ≤ (0, 1, 1, 1); (0, 0) ≤ (0, 1) и (0,1) ≤ (1, 1); 0 ≤ 0 и 0 ≤ 1, и 1 ≤ 1.

Вывод: система функций А является полной, т. к. в каждом из столбцов критериальной таблицы есть хотя бы один «–».

Задания

Для аудиторных занятий

1. Построив таблицы для соответствующих функций, записать их в векторной форме. Выяснить, эквивалентны ли формулы f и g:

а) f = x Ú y ~ х и g = (x ® y) Ù y; б) f = x (y ® z) и g = x ® (y ç zx).

2. С помощью табличного представления задать значения следующих булевых функций:

а) f() = (х ₂ ® х ₁)(х ₂ ¯ х ₂); б) f() = (х ₂ ~ х ₁)(х ₁| х ₂);

в) f() = (х ₁ Å х ₂) ® х ₃)×ù(х ₃ ® х ₂);

г) f() = (х ₁ Ú х ₂ Ú ) ® (х ₁× х ₂| ) Å (х ₂ ® х ₁)× .

3. С помощью векторного представления задать значения следующих булевых функций:

а) f() = ((х ₂ Ú х ₁) ® х ₁× х ₂ ) Å (х ₁® х ₂) Ù (х ₂ ® х ₂);

б) f() = (х ₁ ® х ₂ х ₃)× (х ₂ ® х ₁ х ₃) Ú (х ₁ ~ х ₂).

4. Указать все фиктивные переменные у функции f:

а) f() = (1, 0, 1, 0, 1, 0, 1, 0); б) f() = (0, 1, 1, 0, 0, 1, 1, 0);

в) f() = (1, 1, 1, 1, 0, 1, 1);

г) f() = (1, 0, 1, 1, 0, 1, 0, 1, 1, 0, 1, 1, 0, 1, 0, 1);

д) f() = (0, 1, 0, 1, 1, 1, 1, 1, 0, 0, 1, 1, 1, 1, 1).

5. Указать все фиктивные и существенные переменные у функции f:

а) f() = (х ₂ ® х ₁)(х ₂ ¯ х ₂); б) f() = (х ₂ ~ х ₁)(х ₁| х ₂);

в) f() = (х ₁ Å х ₂) ® х ₃)×ù(х ₃ ® х ₂);

г) f() = (х ₁ Ú х ₂ Ú ) ® (х ₁× х ₂| ) Å (х ₂ ® х ₁)× .

6. Перечислить существенные переменные у следующих функций:

а) f() = ((х ₂ Ú х ₁) ® х ₁× х ₂) Å (х ₁ ® х ₂)(х ₂ ® х ₂);

б) f() = (х ₁ ® х ₂ х ₃)× (х ₂ ® х ₁ х ₃) Ú (х ₁ ~ х ₂).

7. Какие значения принимает булева функция двух переменных для x ₁ Å x ₂?Как называется эта функция?

8. Выяснить, является ли самодвойственной и монотонной функция f:

f = x ₁ x ₂ Ú x ₁ x ₃ Ú x ₃ x ₂.

9. Выяснить, полна ли система функций:

А = { xy, x Ú y, x Å y Å z Å 1}.

Для самостоятельной работы

1. Построив таблицы для соответствующих функций, записать их в векторной форме. Выяснить, эквивалентны ли формулы f и g:

а) f = xy ® х и g = xy ® y; б) f = xy Ù z и g = x ® (y ç zx).

2. С помощью табличного представления задать значения следующих булевых функций:

а) f() = (х ₂ ~ х ₁)(х ₂ ¯ х ₂); б) f() = (х ₂ ® х ₁)(х ₁| х ₂);

в) f() = (х ₁ Å х ₂) ® ù х ₃)× (х ₃ ® х ₂);

г) f() = (х ₁Ú х ₂| ) Å (х ₁× х ₂ Ú ) ® (х ₂ ® х ₁)× .

3. Указать все фиктивные переменные у функции f:

а) f() = (1, 0, 1, 0, 1, 0, 1, 1); б) f() = (0, 1, 0, 0, 0, 1, 1, 0);

в) f() = (1, 0, 1, 1, 0, 1, 1); г) f() = (1, 1, 1, 1, 0, 1, 0, 1, 1, 0, 1, 1, 0, 0, 0, 1); д) f() = (1, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 0).

4. Указать все фиктивные и существенные переменные у функции f:

а) f() = (х ₂ ~ х ₁)(х ₂ ¯ х ₂); б) f() = (х ₂ ® х ₁)(х ₁| х ₂);

в) f() = (х ₁ Å х ₂) ® х ₃)×ù(х ₃ ~ х ₂);

г) f() = (х ₁ ~ х ₂ Ú ) ® (х ₁× х ₂| ) Å (х ₂ ® х ₁)× .

5. Перечислить существенные переменные у следующих функций.

а) f() = ((х ₂ ~ х ₁) ® х ₁× х ₂) Å (х ₁ ® х ₂)(х ₂ ® х ₂);

б) f() = (х ₁ ~ х ₂ х ₃)× (х ₂ ® х ₁х₃) Ú (х ₁ ~ х ₂).

6. С помощью векторного представления задать значения следующих булевых функций:

а) f() = (х ₂ ® х ₁× х ₂) Ù (х ₁ ® х ₂) Å (х ₂ ® х ₂);

б) f() = (х ₁ ® х ₂ Å х ₃)× (х ₂ ® х ₁ Ú х ₃) Ú (х ₁ ~ х ₂).

7. Какие значения принимает булева функция двух переменных для x ₁ Å x ₂? Как называется эта функция?

8. Выяснить, является ли самодвойственной и монотонной функция f

f = x ₁ ® x ₂ Ú x ₁ x ₂ ~ 1.

9. Выяснить, полна ли система функций:

А = { xy, x Ú y, x Å y, xy Ú yz Ú zx }.

Литература

1. Гаврилов, Г. П. Задачи и упражнения по курсу дискретной математики: учеб. пособие / Г. П. Гаврилов, А. А. Сапоженко. – М.: Наука, 1992 – 408 с.

2. Горбатов, В. А. Фундаментальные основы дискретной математики / В. А. Горбатов. – М.: Наука, 2000. – 544 с.

3. Нефедов, В. Н. Курс дискретной математики: учеб. пособие / В. Н. Нефедов, В. А. Осипова. – М.: Изд-во МАИ, 1992. – 264 с.

4. Новиков, Ф. А. Дискретная математика для программистов: учебник для вузов / Ф. А. Новиков. – СПб.: Питер, 2001. – 304 с.

Дата добавления: 2017-02-01