Контрольні запитання

1. Що таке відображення, функція, взаємнооднозначне відображення?

2. Що таке область визначення та множина значень функції?

3. Які є способи задання функції, їх основні характеристики?

4. Яка функція називається оберненою?

5. Яка функція називається складеною, що таке проміжний аргумент?

6. Які функції називаються основними елементарними, елементарними?

7. Назвати основні класи елементарних функцій.

8. Що називається числовою послідовністю?

9. Дати означення границі числової послідовності.

10. Яка послідовність є нескінченно малою, нескінченно великою?

11. Сформулювати основні теореми про границю числової послідовності.

12. Сформулювати і довести теорему про взаємозв’язок між нескінченно великими та нескінченно малими послідовностями.

Тема 1.2. Границя функції та її властивості. Перша та друга важливі границі

Мета. Розширити знання учнів з теми «Границя функції», доповнити їх поняттям чудових границь та прикладами їх застосування. Дати основні теореми для обчислення границь елементарних функцій.

План.

1. Поняття границі функції. Односторонні границі.

2. Нескінченно малі та нескінченно великі функції.

3. Основні теореми про границю функції.

4. Перша та друга важливі границі.

1. Розглянемо поняття околу точки х.

Околом точки х₀ називається будь- який проміжок (a, b), що містить цю точку.

d- околом точки х₀ називається інтервал (х₀-d; х₀+d), деd>0.

Околом плюс нескінченно віддаленої точки на прямій (позначатимемо її +Ґ), називатимемо всякий інтервал (b;+Ґ), деb>0.

Околом мінус нескінченно віддаленої точки на прямій (позначатимемо її -Ґ), називатимемо всякий інтервал (-Ґ; -a), де a>0.

Нехай функція f(x) визначена в деякому околі точки х₀, крім можливо самої точки х₀.

Означення: Число А називається границею функції f(x) в точці х₀ (при х®х₀), якщо для довільно вибраного e>0 можна вказати таке d>0, що для всіх х, що задовольняють умову 0<|x-x₀|<d, виконується нерівність |f(x)-A|<e. Позначаємо .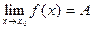

З геометричної точки зору це означає, що для будь - якого e можна вказати такий d-окіл, що якщо всі х з цього околу графік цієї функції буде лежати в стрічці шириною 2e, від А-e до А+e.

Нехай функція f(x)визначена в околі (b;+Ґ) плюс нескінченно віддаленої точки. Число А називається границею функції f(x) в плюс нескінченно віддаленій точці, коли для довільно вибраного e>0 можна вказати таке х(e)іb, що для всіх х, що задовольняють умову х(e)<x<+Ґ випливає нерівність |f(x)-A|<e. Позначаємо або f(x)®A (x®+Ґ).

Аналогічно, нехай функція f(x)визначена в околі (-Ґ;-a) мінус нескінченно віддаленої точки. Число А називається границею функції f(x) в мінус нескінченно віддаленій точці, коли для довільно вибраного e>0 можна вказати таке х(e)Ј-a, що для всіх х, що задовольняють умову -Ґ< x< х(e) випливає нерівність |f(x)-A|<e.

Позначаємо або f(x)®A (x®-Ґ).

Якщо функція f(x) має у плюс і мінус нескінченно віддалених точках однакові границі, то в цьому випадку символічний запис має вигляд .

Нехай функція f(x) визначена на проміжку (х₀; х₀+d₁) (на проміжку (х₀-d₁; х₀)), де d₁>0. Число А називається правою (лівою) границею функції f(x) в точці х₀, якщо для довільно вибраного e>0 існує таке d>0, що з нерівностей 0<x-x₀<d (0<x₀-x<d), випливає нерівність |f(x)-A|<e. Позначаємо (). Запис х®х₀-0 (х®х₀+0) означає, що точка х прямує до точки х₀ справа (зліва). Права та ліва границі функції називаються односторонніми границями функції в точці. Наступна теорема встановлює залежність між правою і лівою та границею функції в точці.

Теорема. Для того, щоб функція f(x) мала границю в точці х₀, необхідно і досить, щоб у цій точці функція f(x) мала праву і ліву границю і щоб права границя дорівнювала лівій.

2. Функція a(х) називається нескінченно малою при х®х₀ (х®Ґ), якщо .

Теорема 1. Якщо a(х) і b(х) нескінченно малі функції при х®х₀ (х®Ґ), то їх сума (a(х)+b(х)) теж нескінченно мала функція при х®х₀ (х®Ґ).

Доведення.

Нехай при х®х₀: , . Для будь- якого >0 знайдеться d₁ таке, що при 0<|x-x₀|<d₁, випливає |a(х)|< . Для цього ж >0 знайдеться d₂ таке, що при 0<|x-x₀|<d₂, випливає |b (х)|< . Позначимо d- менше з двох чисел d₁, d₂. Тоді з нерівності 0<|x-x₀|<d, випливає |a(х)+b(х)| Ј |a(х)|+ |b (х)|< + =e. А це означає, що сума двох нескінченно малих функцій є нескінченно мала функція.

Теорема справедлива і для скінченного числа доданків.

Аналогічно доводяться теореми.

Теорема 2. Добуток нескінченно малої функції a(х) при х®х₀ (х®Ґ), на функцію, обмежену при х®х₀ (х®Ґ) є функція нескінченно мала при х®х₀ (х®Ґ).

Наслідок 1. Добуток двох нескінченно малих функцій при х®х₀ (х®Ґ) є функція нескінченно мала при х®х₀ (х®Ґ).

Наслідок справедливий і для скінченного числа множників.

Наслідок 2. Добуток нескінченно малої функції a(х) при х®х₀ (х®Ґ), на сталу функцію є функція нескінченно мала при х®х₀ (х®Ґ).

Теорема 3. Частка від ділення нескінченно малої функції a(х) при х®х₀ (х®Ґ), на функцію f(x), границя якої не дорівнює нулю при х®х₀ (х®Ґ), є функція нескінченно мала при х®х₀ (х®Ґ).

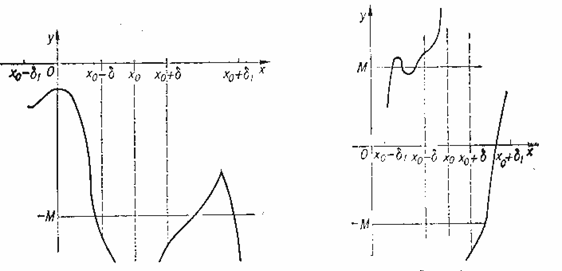
Функція f(x) називається нескінченно великою при х®х₀ (х®Ґ), якщо для будь- якого як завгодно великого числа М можна вказати таке число d>0, що для всіх х, які задовольняють умову 0<|x-x₀|<d, виконується нерівність |f(x)|>M. Позначаємо .

Якщо функція є нескінченно великою при х®х₀ (х®Ґ) і набуває лише додатніх значень, то використовуємо позначення , якщо ж функція є нескінченно великою при х®х₀ (х®Ґ) і набуває лише від’ємних значень, то використовуємо позначення .

Справедлива наступна теорема.

Якщо функція f(x) є нескінченно великою при х®х₀ (х®Ґ), то функція 1/f(x) є функцією нескінченно малою при х®х₀ (х®Ґ). І навпаки, якщо функція a(x) є нескінченно малою при х®х₀ (х®Ґ) і не перетворюється в нуль, то функція 1/a(x) є функцією нескінченно великою при х®х₀ (х®Ґ).

3. Основні теореми про границю.

Теорема 1. Якщо існує границя функції f(x) при х®х₀ (х®Ґ), то ця границя єдина.

Теорема 2. Якщо 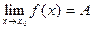, то функцію можна записати у вигляді f(x)=A+a(x), де a(x)- нескінченно мала функція при х®х₀ (х®Ґ).

Доведення.

Нехай 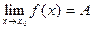, тобто для довільно вибраного e>0 можна вказати таке d>0, що для всіх х, що задовольняють умову 0<|x-x₀|<d, виконується нерівність |f(x)-A|<e. Позначимо f(x)-A=a(x), тоді |a(x)|<e. А це означає, що a(х)- нескінченно мала функція при х®х₀ (х®Ґ).

Справедлива і обернена теорема:

Теорема 3. Якщо функцію можна представити у вигляді f(x)=A+a(x), де a(x)- нескінченно мала функція при х®х₀ (х®Ґ), то .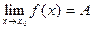

Теорема 4. Якщо існують скінченні границі ; , то існує також границя суми для цих функцій і границя суми дорівнює сумі границь цих функцій: + .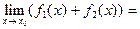

Доведення.

На основі теореми 2 можемо позначити f₁(x)=A₁+a₁(x) і f₂(x)=A₂+a₂(x), де a₁(x) і a₂(x) - нескінченно малі функції при х®х₀. Тоді f₁(x) + f₂(x)=A₁+a₁(x)+ +A₂+a₂(x)= A₁+A₂+a₁(x)+ a₂(x), останні два доданки є нескінченно малою функцією. а це означає, що 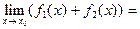A₁+A₂. Теорему доведено.

Теорема справедлива і для скінченного числа доданків.

Теорема 5. Якщо існують скінченні границі ; , то існує також границя добутку для цих функцій при х®х₀ і границя добутку дорівнює добутку границь цих функцій: .

Доведення аналогічне доведенню теореми 4.

Наслідок 1. Сталий множник можна винести за знак границі: с .

Наслідок 2. Якщо задано функцію виду , де nОN, то = .

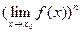Теорема 6. Якщо існують скінченні границі ; , причому А₂№0, то існує також границя частки для цих функцій при х®х₀, причому границя частки дорівнює частці границь цих функцій: / .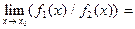

Доведення абсолютно аналогічне доведенню теореми 4.

Вище написанні теореми проведенні для випадку границі при х®х₀. Цілком аналогічно доводяться теореми 2-6 для випадку при х®Ґ.

Основні теореми про границю спрощують обчислення границь функцій, варто лише звести функцію за їх допомогою до якогось з стандартних виглядів (чи важливих границь, чи границь, які легко обчислюються).

Деколи зручно використовувати наступні властивості (подамо їх без доведення), які спрощують перехід до границь в нерівностях.

Теорема 7. Якщо для всіх х з деякого околу точки х₀ виконується нерівність u(x)Јf(x)Јv(x) і 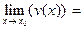А, то А.

Аналогічна теорема справедлива і для випадку коли х®Ґ.

Теорема 8. Якщо для всіх х з деякого околу точки х₀ виконується нерівність f(x)і0,то .

Теорема 9. Якщо для всіх х з деякого околу точки х₀ виконується нерівність u(x)Ј v(x), то .

4. Теорема 1. Справедлива рівність .

Доведення. Якщо х - кут, виміряний у радіанах, 0<x<p / 2, то для площ трикутника ОАВ, сектора ОАВ і трикутника ОСВ

правильні нерівності:

S_DOAB<S_{сект. ОАВ}<S_DOCB , або .

Скоротимо на і поділимо почленно на sin x, звідки

і . Помножимо на (-1) і додамо 1 до кожної частини, отримавши: .

Розглянемо . Тобто отримаємо . Ця нерівність справедлива також і для хО(-p / 2; 0) (Доведення проводимо, замінивши х на -х). Отже, справедлива для всіх хО(-p / 2; p / 2).

Очевидно, що . Тому (за теоремою 7 п.4) . Використовуючи теореми про границю сталого числа та границю суми, отримуємо . Теорему доведено.

Така границя називається в математиці Першою важливою границею або Першою чудовою границею.

Розглянемо числову послідовність .

Теорема 2. Числова послідовність з загальним членом має границю при n®Ґ, і ця границя міститься між числами 2 і 3.

Доведення.

Для довільного nОN справедливий біноміальний розклад

.

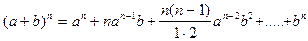Тому

.

Рівність 1Ч2Ч3Ч4Ч....Ч(n-1)Чn=n! (факторіал числа n). Таким чином ми отримали послідовність

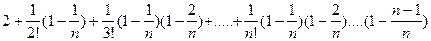. (1)

Оцінимо її:

; ; ;........; .

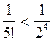З послідовності (1) видно, що y_n і 2. А, оскільки, y_n< , то y_n<2+ =3. Так як послідовність обмежена і зростаюча, то вона має границю, яка розміщена між 2 і 3.

В математиці таке число, яке є границею заданої послідовності позначають e і називають числом Ейлера. е=2,7182.....

На основі теореми 2 доводиться наступне твердження

Теорема 3. Правильна рівність .

Границя з теореми 3 називається Другою важливою або Другою чудовою границею.

Наслідок. Правильні рівності

а) ;

б) ;

в) .

Дата добавления: 2017-02-01