Тема 1.3. Неперервність функції в точці

Контрольні запитання

1. Що таке окіл точки, плюс та мінус нескінченно віддалених точок?

2. Дайте означення границі в цих точках.

3. Дати означення правої та лівої границі.

4. Сформулювати критерій існування границі функції в точці.

5. Дати означення нескінченно малої та нескінченно великої функцій.

6. Сформулювати і довести властивості нескінченно малих функцій.

7. Сформулювати і довести теорему про взаємозв’язок між нескінченно малими та нескінченно великими функціями.

8. Сформулювати і довести основні теореми про границю функцій.

9. Сформулювати і довести теорему про першу важливу границю.

10. Сформулювати і довести теорему про другу важливу границю.

Мета. Розглянути поняття неперервності функції, класифікувати точки розриву, означити операції над наперервними функціями.

План.

1. Неперервність функції в точці.

2. Арифметичні операції над неперервними функціями.

3. Точки розриву та їх класифікація.

4. Властивості функцій, неперервних на відрізку.

1. Функція f(x), визначена в околі точки х₀ називається неперервною в точці х₀, якщо

Більш докладно умову неперервності функції f(x) вточці х₀ можна розписати так:

1) функція f(x) повинна бути визначена в околі точки х₀, в тому числі і в самій точці х₀.

2) в точці х₀ вона повинна мати границю.

3) ця границя має дорівнювати значенню функції в точці х₀.

На «мові e-d» неперервність означається так: Функція f(x), визначена в околі точки х₀ називається неперервною в точці х₀, якщо для будь- якого числа e>0 існує таке d>0, що з нерівності |х-х₀|<d випливає нерівність |f(х) - f(х₀)|<e. Зрозуміло, що |х-х₀|>0.

Поняття неперервності функції можна сформулювати і на «мові приростів».

Приростом аргументу х в точці х₀ називається різниця х-х₀ і позначається Dх.

Приростом функції f(x) вточці х₀ називається різниця f(х) - f(х₀) і позначається Df(х₀).

Приріст аргументу та приріст функції можуть бути як додатними, так і від’ємними величинами. Приріст функції, крім того може дорівнювати нулеві. Якщо точка х₀ - фіксована, то приріст функції є функцією від Dх. Якщо х®х₀, то Dх®0. Справедливе також обернене твердження.

Отже, означення неперервності функції в точці х₀ можна сформулювати так:

функція f(x), визначена в околі точки х₀, називається неперервною в цій точці, якщо .

Іншими словами, функція f(x), визначена в околі точки х₀, називається неперервною в цій точці, якщо нескінченно малим приростам аргументу відповідають нескінченно малі прирости функції.

Всі означення рівносильні між собою.

Зауважимо, що , отже, символ неперервної функції і границі можна переставляти місцями, тобто під знаком неперервної функції можна переходити до границі.

Можна довести таку теорему:

Кожна основна елементарна функція є неперервною в усіх точках, в яких вона визначена.

2. Теорема 1. Якщо функції f(x) і j(х) неперервні в точці х₀, то в цій точці неперервні функції:

f(x) + j(х); f(x) - j(х); f(x) Ч j(х); f(x) / j(х)

(остання при допоміжній умові j(х₀)№0).

Доведення. Доведемо, наприклад, неперервність частки. Нехай . Знайдемо границю функції F(x) в точці х₀. Оскільки функції f(x) та j(х) - неперервні в точці х₀, то ; Оскільки j(х₀)№0, то за теоремою про границю частки існує границя функції F(x) в точці х₀, причому , тобто .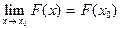

А це означає, що функція F(x)- неперервна в точці х₀.

Аналогічно доводиться неперервність функцій f(x)+j(х); f(x)-j(х); f(x)Чj(х). Тут використовують означення неперервної функції і теореми про границю суми, різниці та добутку двох функцій відповідно.

Наслідок 1. Добуток та сума скінченного числа неперервних функцій є функція неперервна.

Наслідок 2. Оскільки основні елементарні функції є неперервними в кожній точці, де вони існують, то елементарні функції є неперервними в кожній точці, де вони існують.

Справедлива також Теорема 2.

Якщо функція f(x)- неперервна в точці х₀О(а; b), а функція x=j(t) неперервна в точці t₀О(a;b), причому x₀=j(t₀), то складена функція f(j(t))- що є функцією від t - неперервна в точці t₀.

Доведення.

Задамо число e>0. Тоді, внаслідок неперервності функції f(x) в точці х₀, для числа e>0 існує число d₁>0 таке, що з нерівності

|х-х₀|<d₁ (1)

випливає нерівність

|f(х) - f(х₀)|<e. (2)

Для знайденого вище числа d₁>0, внаслідок неперервності функції x=j(t) в точці t₀ існує число d>0 таке, що з нерівності

|t-t₀|<d (3) випливає нерівність

|х-х₀|= |j(х) - j(х₀)|< d₁. (4)

Якщо виконана нерівність (3), то виконана (4), але (4) випливає з (1). Таким чином, для будь- якого числа e>0 існує число d>0 таке, що з нерівності (3) випливає нерівність

|f(х) - f(х₀)|<e.

А це означає, що складена функція, задана в теоремі, неперервна в точці t₀.

Теорему доведено.

Функція f(x) називається неперервною в інтервалі (a; b), скінченному чи нескінченному, якщо вона неперервна в кожній точці цього інтервалу.

3. Функція f(x) називається неперервною в точц і х₀ справа (зліва), якщо

().

Таким чином, для неперервності функції f(x) в точці х₀ справа (зліва) слід перевірити три умови:

1) функція f(x) має бути визначена на піввідрізку [x₀; x₀+h) (у півінтервалі (x₀-h; x₀]), де h>0;

2) у точці х₀ функція має праву (ліву) границю;

3) ця права (ліва) границя повинна дорівнювати значенню функції f(x) в точці х₀.

На мові «e-d» означення неперервності справа (зліва) можна дати так: функція f(x), визначена на піввідрізку [x₀; x₀+h) (у півінтервалі (x₀-h; x₀]), де h>0 називається неперервною справа (зліва), якщо для будь- якого e>0 можна знайти таке d>0, що з нерівності 0Јх-х₀<d (0Јх₀-х<d) випливає нерівність |f(x)-f(x₀)|<e.

З теореми про границю суми, добутку, різниці, частки двох функцій відносно множини та означення неперервності функції справа (зліва) випливає, що сума, різниця, добуток, частка (остання при допоміжній умові, що функція, яка стоїть в знаменнику, не рівна нулю в точці х₀) є функції неперервні в точці х₀ справа (зліва).

З означення неперервності функції в точці х₀ справа і зліва і теореми- критерію існування границі випливає твердження:

Теорема. Для того щоб функція f(x) була неперервною в точці х₀, необхідно і досить, щоб функція f(x) була неперервна в точці х₀ і справа, і зліва.

3. Нехай функція f(x) визначена в околі точки х₀, крім можливо самої точки х₀. Якщо функція f(x) не є неперервною в цій точці, то кажуть, що точка х₀ є точкою розриву, а сама функція є розривною в цій точці.

З означення зрозуміло, що функція буде розривна, якщо виконуватиметься хоча б одна з умов:

1) функція f(x) не визначена в точці x₀; хоч у всіх інших точках околу вона визначена;

2) у точці х₀ не існує границі функції f(x);

3) границя функції f(x), якщо вона існує, не дорівнює значенню функції f(x) в точці х₀.

Функція f(x) визначена на піввідрізку [x₀; x₀+h) (у півінтервалі (x₀-h; x₀]), за винятком можливо самої точки х₀, що не є неперервною в точці х₀ справа(зліва), називається розривною в точці х₀ справа (зліва), а сама точка х₀ називається точкою розриву функції справа (зліва).

1) функція f(x) не визначена в точці x₀; хоч у всіх інших точках інтервалу (x₀; x₀+h) (інтервалу (x₀-h; x₀)), вона визначена;

2) у точці х₀ не має правої (лівої) границі функції f(x);

3) права (ліва) границя функції f(x), якщо вона існує, не дорівнює значенню функції f(x) в точці х₀.

Точка х₀ розриву функції f(x) називається точкою розриву першого роду, якщо в цій точці існує і права, і ліва границі функції f(x).

Точка х₀ розриву функції f(x) називається точкою розриву другого роду, якщо в цій точці не існує хоч одна з односторонніх границь функції f(x). (або вони нескінченні)

Якщо х₀ - точка розриву першого роду функції f(x) і права границя функції в цій точці не рівна лівій границі цієї функції, то абсолютну величину різниці правої і лівої границь функції в цій точці називають стрибком функції в точці х₀.

Аналогічно діляться і точки розриву функції справа та зліва.

Справедливе твердження

Теорема. Функція f(x), монотонна на проміжку <a; b>, може мати лише точки розриву першого роду.

Якщо точка х₀ є точкою розриву першого роду і , то ця точка називається точкою усувного розриву.

4. Властивості функцій, неперервних на відрізку.

Функція називається неперервною на інтервалі, якщо вона неперервна в кожній точці цього інтервалу.

Функція називається неперервною на відрізку [a; b], якщо вона неперервна в кожній точці інтервалу (a; b) і неперервна в точці а справа і в точці b зліва.

Теорема 1. Функція неперервна на відрізку є обмеженою на цьому відрізку.

Теорема 2. Якщо f(x) - неперервна на відрізку [a; b], то вона досягає на цьому відрізку найбільшого та найменшого значення.

Теорема 3. Якщо f(x) - неперервна на відрізку [a; b] і на його кінцях приймає значення різних знаків, то існує хоч би одна точка х в середині відрізка, в якій f(x)=0.

Теорема 4. Якщо f(x) неперервна на відрізку [a; b], і f(a)=A, f(b)=B, то яке б не було число С таке, що A<C<B, знайдеться точка с така, що сО [a; b], f(c)=C.

Наслідок. Якщо f(x) - неперервна на відрізку [a; b] і m<C<M, то знайдеться така точка сО [a; b], для якої f(c)=C.

Дата добавления: 2017-02-01