Іі. Деякі важливі типи випадкових процесів

Дисперсія випадкового процесу.

Математичне сподівання або середнє значення випадкового процесу

Нехай x (t) — випадковий процес.Зафіксуємо аргумент t Î T. При цьому одержимо випадкову величину x_t. Обчислимо її математичне сподівання (вважаючи, звичайно, що така характеристика для вказаної величини існує). При цьому одержимо відповідне числове значення, що залежить від обраної величини t. Змінюючи t в межах T, одержимо деяку функцію на T. Позначимо її m (t). Таким чином, маємо

m (t) = Мx_t, t Î T. (1.1)

Функцію, визначену у вказаний спосіб, і будемо називати математичним сподіванням або середнім значенням випадкового процесу (надалі для її позначення вживаються і інші літери, окрім m (t)).

Як і в попередньому випадку, зафіксуємо аргумент t та обчислимо дисперсію одержаної випадкової величини x_t (знову ж - таки вважаючи, що вказана характеристика x_t існує; надалі зауважень щодо існування розглядуваних характеристик робити не будемо, якщо тільки така вказівка не буде мати спеціальну мету). Оскільки обчислена величина залежить від t, то знову маємо деяку функцію на множині T, яку позначимо d (t). Таким чином, маємо за означенням

d (t) = Dx_t, t Î T. (1.2)

1.7. Коваріаційна (автоковаріаційна) та кореляційна (автокореляційна) функції випадкового процесу

Зафіксуємо два значення часу, які позначимо s та t. Цього разу одержимо дві випадкові величини: x_s та x_t. Розглянемо їхню коваріацію, тобто величину

cov (x_s, x_t) = М x_s x_t – Мx_s Мx_t = М (x_s – М x_s)(x_t – М x_t).

При зміні s, t в межах T одержимо таким чином функцію пари аргументів (на T ´ T), яку позначимо c (s, t):

c (s, t) = cov (x_s, x_t). (1.3)

Функцію C (s, t) будемо називати коваріаційною або автоковаріаційною функцією процесу x (t). Інколи замість коваріаційної функції зручно розглядати так звану кореляційну (або автокореляційну) функцію процесу k (s, t), яка також є функцією двох аргументів і визначається рівністю 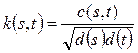(1.4)

1.8. Елементарний випадковий процес – це функція деякого аргументу, що задана явним виразом, причому у її вираз входять випадкові параметри. Приклади:

1) x (t)= x ₀ e^-t, t > 0, 2) x (t)= at + x ₀; a = const;

x ₀ - випадкова величина. x ₀ - випадкова величина.

На малюнках подано кілька реалізацій двох вказаних випадкових процесів.

Дата добавления: 2017-02-01