Гауссівські (гауссові) випадкові процеси

Процеси з незалежними приростами

Процеси з незалежними значеннями

Процесом з незалежними значеннями називається випадковий процес, для якого величини x (t ₁), x (t ₂), …, x (t_n) є взаємно незалежними для довільних t ₁ < t ₂ < … < t_n з Т.

Завдання. Переконатися, що всі скінченновимірні розподіли таких процесів визначаються їх одновимірними розподілами.

Процес x (t), t Î Т, називається процесом з незалежними приростами, якщо для будь-яких моментів часу t ₀ < t ₁ < … < t_n (t_і Î Т, і = 1,…, n) випадкові величини x (t ₀), x (t ₁)– x (t ₀),…, x (t_n)– x (t_{n –1}) є взаємно незалежними.

Завдання. Переконатися, що скінченновимірні розподіли процесу з незалежними приростами визначаються його розподілами порядку не вище другого.

Зауваження. Один з варіантів розв’язання попереднього завдання міститься в [, с.69, 70]

Дійсний процес x (t), t Î Т називають гауссівським або гауссовим, якщо для будь-яких t ₁,…, t_n з T вектор (x (t ₁), x (t ₂),…, x (t_n)) є нормально розподіленим випадковим вектором (див. [,розділ 1.13] або нижче рівність (1.5)).

Зауваження. Згідно з вказаним означенням нормально розподілені випадкові вектори не обов’язково мають щільність розподілу. Випадок, коли вони мають зазначену щільність, зветься невиродженим. Надалі зустрічаються гуссівські процеси лише з невиродженими скінченновимірними розподілами. Це означає, що вектор (x (t ₁), x (t ₂),…, x (t_n)) при будь-яких n та t ₁,…, t_n має щільність розподілу

, (1.5)

де ¢ — знак транспонування матриці або вектору, x = (x ₁, x ₂,…, x_n)¢ — n -вимірний вектор-стовпчик, m — математичне сподіваннявектору (x (t ₁), x (t ₂),…, x (t_n)), S – його дисперсійна (коваріаційна) матриця (див. [, 1.13]), так що

m = (m ₁, m ₂,…, m _n)¢ = (Мx (t ₁), Мx (t ₂),…, Мx (t_n))¢,

S = || s _іj || = || cov (x (t_і), x (t_j)|| = || М (x (t_і)× x (t_j)) – Мx (t_і)× Мx (t_j)||

Таким чином, всі параметри функції 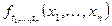визначаються функцією середнього значення і коваріаційною функцією процесу x (t).

Питання до означення. Розподілами якого найменшого порядку визначаються всі скінченновимірні розподіли гауссівського випадкового процесу? (Відповідь: 2. Обґрунтуйте цю відповідь).

Дата добавления: 2017-02-01