Класифікація задач математичного програмування

Під загальною задачею математичного програмування розуміють задачу пошуку екстремуму ( чи ) функції

(2.1)

за умов

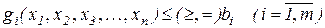(2.2)

де (2.3)

Умови (1.2) називають обмеженнями задачі, а функцію (2.1) – цільовою функцією. При цьому функції і , а також числа вважаються заданими. Крім того, в кожному з обмежень (1.2) зберігається тільки один знак відношення , хоча, в цілому, різні обмеження можуть мати різні знаки. Множина точок, що задовольняє умовам (2.2), (2.3), називається множиною допустимих значень.

Використати класичні методи знаходження умовного екстремуму функції для розв’язання (2.1)–(2.3) практично неможливо, так як екстремум у цій задачі досягається на границі множини допустимих значень. Тому для дослідження задач типу (2.1)–(2.3) створено самостійні теорії і методи.

Математичне програмування поділяється на такі основні розділи: лінійне програмування, нелінійне програмування, стохастичне програмування, динамічне програмування.

Лінійним програмуванням називається розділ математичного програмування, що вивчає задачі типу (2.1)–(2.3), в яких функції і є лінійними, тобто

,

,

де – задані константи, а множина містить точки з невід’ємними компонентами.

Тоді задача математичного програмування має вигляд:

знайти екстремум лінійної функції (форми)

за умов

Особливе місце в лінійному програмуванні посідають задачі лінійного цілочислового програмування, в яких на всі або частину змінних величин накладено додаткову умову цілочисельності. Ця умова випливає з фізичного змісту багатьох практичних задач. Якщо умову цілочисельності накладено на всі змінні, то така задача лінійного програмування називається повністю цілочисловою. Якщо обмеження стосуються тільки частини змінних – частково цілочисловою.

Загальна задача цілочислового лінійного програмування має вигляд:

знайти екстремум лінійної функції

за умов

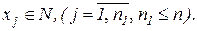
Важливим класом задач цілочислового лінійного програмування є такі задачі, в яких змінні можуть набувати тільки двох значень або .

Нелінійним програмуванням називається розділ математичного програмування, що вивчає задачі типу (2.1)–(2.3), в яких функція або хоча б одна з функцій є нелінійними.

Стохастичним програмуванням називається розділ математичного програмування, який вивчає моделі вибору оптимальних розв’язків у ситуаціях, що характеризуються випадковими величинами.

Задачі стохастичного програмування випливають за умови неточної інформації, невизначеності та ризику.

Динамічним програмуванням називається розділ математичного програмування, який вивчає багатокрокові процеси пошуку розв’язку.

У деяких галузях практичної діяльності доцільно шукати розв’язки не відразу, а послідовно, тобто розв’язок розглядається як процес, що складається з певних кроків, етапів.

Дата добавления: 2017-02-01