Приклад розв’язування задачі

Приклад. Для виготовлення виробів А, В, С підприємство використовує 3 види сировини. Норми витрат сировини на виробництво кожного виду продукції, ціна одного виробу та загальна кількість сировини подані у таблиці 2.33.

Таблиця 2.33 – Вихідні дані

Вид сировини	Норми витрат сировини на 1 виріб	Кількість сировини
Виріб А	Виріб В	Виріб С
Сировина І	1	5	4	315
Сировина ІІ	1	2	1	90
Сировина ІІІ	5	3	4	168
Ціна 1 виробу	3	5	8	-

Скласти план виробництва виробів, при якому загальна вартість всієї виготовленої продукції буде максимальною.

Розв’язання

Загальна виручка: → max

Обмеження:

Зводимо задачу до канонічного вигляду:

Запишемо рівняння у векторній формі:

Р₁х₁ + Р₂х₂ + Р₃х₃ + Р₄х₄ + Р₅х₅ + Р₆х₆= Р_0,

, , , , , ,

Складаємо першу симплекс-таблицю (таблиця 2.34):

Таблиця 2.34 – Перша симплекс-таблиця

і	Базис		План
х1	х2	х3	х4	х5	х6
	х4	0	315	1	5	4	1	0	0	78,75
	х5	0	90	1	2	1	0	1	0	90
	х6	0	168	5	3	4	0	0	1	42
∆	-	-	0	-3	-5	-8	0	0	0

Елементи останнього рядка симплекс-таблиці є оцінками _j, за допомогою яких опорний план перевіряють на оптимальність. Їх визначають так:

; і т.д.

У стовпчику «План» рядка _j записуємо значення, яких набувають рівності системи обмежень (у канонічному вигляді) при умові, що вільні змінні дорівнюють нулю.

Після заповнення першої симплекс-таблиці опорний план перевіряємо на оптимальність. Для цього застосовують теорему оптимальності. Тобто перевіряють чи задовольняють елементи рядка _j відповідну умову. А саме, для задачі на максимум всі (для задачі на мінімум ).

Якщо ж в оцінковому рядку є хоча б одна оцінка, що не задовольняє умову оптимальності (від’ємна в задачі на max або додатна в задачі на min), то опорний план є неоптимальним. Отже, треба перейти до наступного оптимального плану задачі. Для цього визначимо, яку змінну будемо виводити з базису, а яку вводити.

У оцінковому рядку _j є три від’ємні оцінки , та . Серед цих чисел виберемо найбільше за абсолютною величиною: .

Тобто, в базис будемо вводити змінну, яка відповідає цьому стовпчику: . Стовпчик із змінною є розв’язувальний.

Визначимо змінну, яку виводитимемо з базису. Обчислимо співвідношення елементів стовпчика «План» до відповідних елементів розв’язувального стовпчика:

, , .

Виберемо найменше значення θ, яке вказує на змінну, що виводиться з базису. Тобто, рядок із змінною є напрямним.

На перетині розв’язувального стовпчика та напрямного рядка розміщений розв’язуваний елемент: 4.

Заповнюємо нову симплекс-таблицю 2.35.

Таблиця 2.35 – Друга симплекс-таблиця

і	Базис		План
х1	х2	х3	х4	х5	х6
	х4	0	147	-4	2	0	1	0
	х5	0	48			0	0	1
	х3	42	42			1	0	0
∆	-		336	7	1	0	0	0	2

Спершу у нову симплекс-таблицю заносять елементи напрямного стовпчика поділені на розв’язувальний елемент. Під розв’язувальним елементом (якщо є порожні клітинки, то і над) записують нулі.

Решту елементів таблиці розраховують за правилом прямокутника:

;

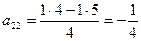і т.д.

Аналогічно розраховуємо дані зі стовпчика «План»: , .

Елементи оцінкового рядку обчислимо за формулою:

.

і т.д.

Після заповнення другої симплекс-таблиці опорний план перевіряємо отриманий план на оптимальність.

У оцінковому рядку для задачі на максимум всі числа повинні бути . Усі числа задовольняють цю умову. Отже, отриманий план є оптимальним.

Таким чином, ми отримали розв’язок задачі: , , , .

Завдання для індивідуальної та самостійної роботи студентів

Приклад. Розв’язати ЗЛП симплекс-методом.

Номер варіант визначається за вказівкою викладача.

1.	16.
2.	17.
3.	18.
4.	19.
5.	20.
6.	21.
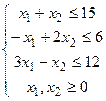
7.	22.
8.	23.
9.	24.
10.	25.
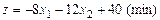
11.	26.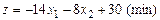
12.	27.
13.	28.
14.	29.
15.	30.

Дата добавления: 2017-02-01