Приклад розв’язування задачі

Приклад 1. Побудувати на площині множину розв’язків (багатокутник) системи лінійних обмежень-нерівностей й геометрично знайти найбільше та найменше значення лінійної функції в цьому багатокутнику (x₁ ³0, x₂ ³0).

Розв’язання

Зобразимо графічно допустимий планів задачі. Замінимо знаки нерівностей на знаки строгих рівностей і побудуємо графіки відповідних прямих (рисунок 2.8).

Рисунок 2.8 – Область допустимих розв’язків

Кожна з побудованих прямих поділяє площину системи координат на дві півплощини. Координати точок однієї з півплощин задовольняють розглядувану нерівність, а іншої — ні. Щоб визначити необхідну півплощину потрібно взяти будь-яку точку і перевірити, чи задовольняють її координати зазначене обмеження. Якщо задовольняють, то півплощина, в якій міститься вибрана точка, є геометричним зображенням нерівності (на рисунку 1.8 відповідна півплощина позначена стрілочкою).

Умова невід’ємності змінних х ₁ ≥ 0, х ₂ ≥ 0 обмежує область допустимих планів задачі першим квадрантом системи координат.

Переріз усіх півплощин, де виконуються відповідні нерівності визначає область допустимих планів задачі. У нашому прикладі це чотирикутник OABC.

Знайдемо найбільше та найменше значення цільової функції.

Для цього побудуємо вектор 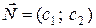, координатами якого є коефіцієнти при змінних у цільовій функції задачі. Вектор завжди виходить із початку координат і напрямлений до точки з координатами (х ₁ = с ₁; х ₂ = с ₂). У нашій задачі вектор . Він задає напрям збільшення значень цільової функції Z.

Побудуємо лінію рівнів. Нехай Z =0. Це буде пряма 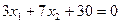(лінія рівнів), яка перпендикулярна до вектора і проходить через початок координат. Оскільки в даному прикладі необхідно визначити найбільше значення цільової функції, то пересуватимемо лінію рівнів паралельно самій собі за напрямом вектора доти, доки не визначимо вершину багатокутника, яка відповідає максимальному плану задачі (остання точка області допустимих розв’язків, якої торкнеться лінія рівнів).

Із рисунку 2.8 видно, що останньою спільною точкою прямої цільової функції та багатокутника OABC є точка В. Для того, щоб знайти координати точки знайдемо перетином яких прямих є ця пряма. На рисунку 2.8 кожна пряма пронумерована відповідно до її розміщення у системи обмежень. Тобто точка В є точкою перетину ІІ та ІІІ прямих.

Тоді координати точки В є розв’язком системи рівнянь. Запишемо рівняння другої та третьої прямих під знаком системи та знайдемо її розв’язок:

Звідси , .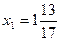

Підставимо отримані координати у цільову функцію та знайдемо максимальне її значення: .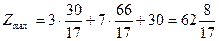

Аналогічно знайдемо точку мінімуму. Пересуватимемо пряму 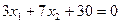паралельно самій собі проти напряму вектора доти, доки не визначимо вершину багатокутника, яка відповідає мінімальному плану задачі (остання точка області допустимих розв’язків, якої торкнеться лінія рівнів).

З рисунку 2.8 видно, що це точка О. Її координати х₁ = 0; х₂ = 0. Тоді .

Приклад 2. Побудувати на площині множину розв’язків (багатокутник) системи лінійних обмежень-нерівностей й геометрично знайти найбільше та найменше значення лінійної функції в цьому багатокутнику (x₁ ³0, x₂ ³0):

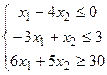
Розв’язання. Записуємо нерівності системи обмежень у вигляді рівнянь, будуємо ці прямі та визначаємо півплощини, де виконуються півплощини. Знаходимо область допустимих розв’язків (рисунок 2.9).

ІІ     6   І     -3 -1 0 4 5 -2 ІІІ  

Рисунок 2.9 – Область допустимих розв’язків

Оскільки множина розв’язків необмежена, то мінімального значення заданої функції немає, тоді записуємо .

Максимальне значення цільова функція набуває у т. А (0;6), тобто

.

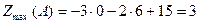Завдання для індивідуальної та самостійної роботи студентів

Приклад. Побудувати на площині множину розв’язків (багатокутник) системи лінійних обмежень-нерівностей й геометрично знайти найбільше та найменше значення лінійної функції в цьому багатокутнику (x₁ ³0, x₂ ³0).

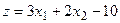
1.	16.
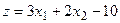
2.	17.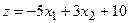
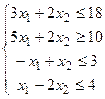
3.	18.
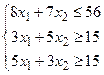
4.	19.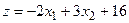
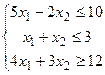
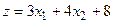
5.	20.
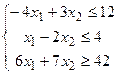
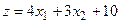
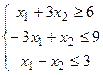
6.	21.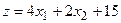
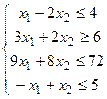
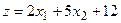
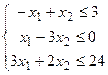
7.	22.
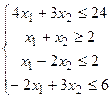
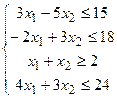
8.	23.
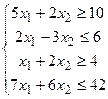
9.	24.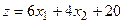
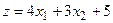
10.	25.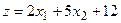
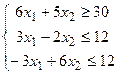
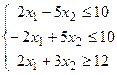
11.	26.
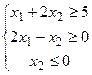
12.	27.
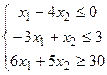
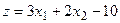
13.	28.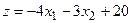
14.	29.
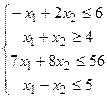
15.	30.

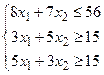
Номер варіант визначається за вказівкою викладача.

Дата добавления: 2017-02-01