Короткі теоретичні відомості

Відведений час: 6 год.

Симплекс-метод

Мета: формувати вміння розв’язувати ЗЛП симплекс-методом.

Завдання для практичного заняття:

1. Пригадайте основні теоретичні питання теми.

2. Орієнтовні запитання та завдання:

- суть симплекс-методу;

- алгоритм симплекс-методу

- назвіть основні поняття, що пов’язані із симплекс-методом (базисні, вільні змінні, розв’язувальний елемент, оцінковий рядок, напрямний стовпчик тощо);

- сформулюйте ознаку оптимальності опорного плану;

- запишіть симплекс таблицю у загальному вигляді;

- як здійснюється перехід від одного опорного плану до іншого.

3. Виконайте індивідуальне завдання.

Симплексний метод або метод послідовного поліпшення плану є універсальним методом, яким можна розв’язувати довільну задачу лінійного програмування.

Алгоритм розв’язування задачі лінійного програмування симплекс-методом:

1. Зведемо задачу лінійного програмування до канонічного вигляду, тобто запишемо у вигляді обмежень-рівнянь з невід’ємними правими частинами.

2. Запишемо задачу лінійного програмування у векторній формі.

Можливі такі випадки:

- після запису задачі у векторній формі в системі обмежень є необхідна кількість одиничних векторів. Тоді початковий опорний план визначається безпосередньо без додаткових дій;

- у системі обмежень немає необхідної кількості одиничних незалежних векторів. Тоді для побудови першого опорного плану застосовують метод штучного базису. (цей метод буде розглянуто в наступній практичній).

Визначені одиничні лінійно незалежні вектори утворюють базис, і змінні задачі, що відповідають їм, називають базисними, а всі інші змінні — вільними.

Щоб отримати початкови й опорний план необхідно всі вільні змінні прирівняти до нуля і тим самим отримаємо значення базисних змінних.

3. Заповнимо симплекс-таблицю (дивись таблицю 2.32).

Таблиця 2.32 – Симплекс-таблиця

У стовпчику таблиці — «Базис» — записують базисні змінні опорного плану, причому в тій послідовності, в якій вони розміщуються в системі обмежень задачі.

Наступний стовпчик симплексної таблиці — «С _баз» — коефіцієнти при базисних змінних у цільовій функції задачі.

У стовпчику — «План» — записують значення базис­них змінних і відшукувані у процесі розв’язування задачі компоненти оптимального плану.

У решті стовпчиків симплексної таблиці, кількість яких відповідає кількості змінних задачі, записують відповідні коефіцієнти з кожного обмеження задачі лінійного програмування.

4. Перевіримо опорний план на оптимальність. При цьому використаємо теорему.

Теорема (ознака оптимальності опорного плану). Опорний план задачі лінійного програмування є оптимальним, якщо для всіх виконується умова

(для задачі на max)

або

(для задачі на min)

Значення оцінок 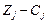визначають за формулою

або безпосередньо із симплексної таблиці як скалярний добуток векторів-стовпчиків «С _баз» та «x_j» мінус відповідний коефіцієнт С_j. Розраховані оцінки записують в окремий рядок симплексної таблиці, який називають оцінковим (розв’язувальним).

Можливі такі випадки:

а) усі оцінки 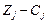задовольняють теорему про ознаку оптимальності опорного плану, тоді роблять висновок, що визначений опорний план є оптимальним;

б) не всі оцінки 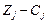задовольняють теорему про ознаку оптимальності опорного плану, тоді необхідно виконати перехід до нового опорного плану задачі і знову здійснити перевірку опорного плану на оптимальність за теоермою.

5. Перейдемо від одного опорного плану до іншого. Необхідно виключити з базису деяку змінну та включити до нього іншу.

Це можна зробити таким чином:

- для того, щоб визначити змінну, яку будемо вводити в базис, треба у розв’язувальному рядку серед оцінок, які не задовольняють ознаку оптимальності опорного плану, вибрати найбільшу за абсолютною величиною (якщо така оцінка єдина, то взяти цю єдину оцінку) і змінну, яка відповідає цьому значенню вводять до базису - відповідний стовпчик симплексної таблиці називають напрямним (розв’язувальним).

- для того, щоб визначити змінну, яку будемо виводити з базису, треба елементи стовпчику «План» поділити на додатні елементи напрямного стовпчика, результати записати у додатковий стовпчик («тетта»), серед отриманих значень вибрати найменше.; відповідну цьому знанню змінну виводять з базису, а даний рядок називають напрямним.

На перетині напрямного стовпчика та напрямного рядка стоїть число, яке називають розв’язувальним елементом.

Щоб заповнити нову симплекс-таблицю треба:

1. У новій симплекс таблиці спочатку заповнюємо два перших стовпчики «Базис» і «С _баз».

2. Заповнимо рядок нової симплекс-таблиці, який відповідає напрямному рядку, для цього поділимо всі елементи напрямного стовпчика на розв’язувальний елемент і запишемо отримані значення у нову симплекс-таблицю.

3. Напрямний стовпчик у новій симплекс-таблиці заповнюють як одиничний, де одиниця стоїть замість розв’язувального елемента.

4. Решту чисел розраховують за допомогою правила прямокутника (або методу Жордана-Гаусса). Для цього необхідно в попередній симплекс-таблиці скласти умовний прямокутник, вершини якого утворюються такими числами:

1 – розв’язувальний елемент;

2 – число, що стоїть на місці елемента нової симплексної таблиці, який ми маємо розрахувати;

3 та 4 – елементи, що розміщуються в двох інших протилежних вершинах умовного прямокутника.

Отримаємо такий умовний прямокутник:

Необхідний елемент нової симплекс-таблиці визначаємо за такою формулою:

.

Аналогічно розраховуємо усі елементи нової симплексної таблиці, у тому числі й елементи стовпчика «План» та оцінкового рядка.

Зауважимо, що елементи оцінкового рядка можна розрахувати і за наведеною раніше формулою. Це дає змогу нам контролювати правильність розрахунків.

Переходи до нового опорного плану продовжують доти доки не буде знайдено оптимальний план або не буде доведено, що такого плану не існує.

Оптимальний план задачі лінійного програмування не існує у такому випадку: якщо при переході одного опорного плану задачі до іншого в напрямному стовпчику немає додатних елементів, тобто неможливо вибрати змінну, яка має бути виведена з базису, то це означає, що цільова функція задачі лінійного програмування є необмеженою й оптимальних планів не існує.

Дата добавления: 2017-02-01