Методические указания к выполнению лабораторной работы на ПК

Результат расчета в ППП ЭВРИКА.

РЕЗУЛЬТАТЫ РАБОТЫ ПРОГРАММЫ В Qbasic

ВИД ПРОГРАММЫ НА ЯЗЫКЕ QBASIC

DECLARE SUB simp (a!, b!, n!, sim!)

DECLARE SUB trap (a!, b!, n!, tr!)

DECLARE SUB pr (a!, b!, n!, prm!)

DECLARE FUNCTION F! (x!)

CLS

INPUT "Введите a= "; a

INPUT "Введите b= "; b

INPUT "Введите e= "; e

n = 2

DO

CALL pr(a, b, n, prm)

CALL pr(a, b, 2 * n, prm1)

n = 2 * n

LOOP UNTIL ABS(prm1 - prm) < e

PRINT "шаг интегрирования h="; (b - a) / n

PRINT "значение интеграла по методу прямоугольника="; prm

PRINT " кол-во шагов для достижения точности Eps ="; n

PRINT

n = 2

DO

CALL trap(a, b, n, tr)

CALL trap(a, b, 2 * n, tr1)

n = 2 * n

LOOP UNTIL ABS(tr1 - tr) < e

PRINT "шаг интегрирования h="; (b - a) / n

PRINT "значение интеграла по методу трапеции="; tr

PRINT " кол-во шагов для достижения точности Eps ="; n

PRINT

n = 2

DO

CALL simp(a, b, n, sim)

CALL simp(a, b, 2 * n, sim1)

n = 2 * n

LOOP UNTIL ABS(sim1 - sim) < e

PRINT "шаг интегрирования h="; (b - a) / n

PRINT "значение интеграла по методу Симпсона="; sim

PRINT " кол-во шагов для достижения точности Eps ="; n

END

FUNCTION F (x)

F = (x ^ 2 * LOG(1 / x)) / (1 - x)

END FUNCTION

SUB pr (a, b, n, prm)

h = (b - a) / n

prm = 0

FOR x = a TO b - h STEP h

prm = prm + F(x)

NEXT x

prm = prm * h

END SUB

SUB simp (a, b, n, sim)

s1 = 0: s2 = 0

h = (b - a) / n

FOR x = a + h TO b - 2 * h STEP 2 * h

s1 = s1 + F(x)

s2 = s2 + F(x + h)

NEXT x

sim = h * (F(a) + 4 * s1 + 2 * s2 + F(b)) / 3

END SUB

SUB trap (a, b, n, tr)

tr = 0

h = (b - a) / n

FOR x = a + h TO b STEP h

tr = tr + F(x)

NEXT x

tr = h * ((F(a) + F(b)) / 2 + tr)

END SUB

Вывод: Значение интеграла, вычисление всеми способами достаточно близки.

1. Подынтегральную функцию варианта задания оформляем как подпрограмму функцию, используя в меню оболочки QuickBasic режим:

FUNCTION F(Х)

F= < функция соответствующего варианта >

END FUNCTION

Запись всех подпрограмм можно осуществить через меню оболочки QuickBasic:

1. Alt - вход в меню

2. EDIT - всплывающее меню редактирования

3. NEW SUB - создание новой подпрограммы
(NEW FUNCTION -создание новой подпрограммы функции)

4. Набираем в диалоговом окне новое имя подпрограммы, например: INTT

5. На экране появляется заготовка для создания подпрограммы:

SUB <имя подпрограммы>

END SUB

6. Приступаем к написанию подпрограммы между ключевыми словами SUB и END SUB

Все вспомогательные подпрограммы объединяются управляющей программой или головным модулем. Переход от текста управляющей программы к текстам подпрограмм происходит при нажатии клавиш
ALT + F1, наоборот - ALТ + F2

Контрольные вопросы

1. Когда используются процедуры?

2. Как создаются подпрограммы, процедуры?

3. Что такое управляющий модуль?

4. Как просмотреть все присоединённые модули?

5. Где объявляются присоединённые подпрограммы? Каким оператором?

6. Какие параметры называются фактические?

7. Какие параметры называются формальные?

8. Как передаются данные из подпрограммы в программу и наоборот?

9. Чем отличаются задачи на интегрирование с заданным числом разбиения отрезка от задачи с заданной точностью вычисления?

10. В чем заключаются численные методы интегрирования?

11. Как реализуется один из методов (по выбору) на QBasic?

12. Как определить погрешность метода?

13. Как осуществляется интегрирование с автоматическим методом выбором шага интегрирования?

Варианты заданий для самостоятельного решения

Задание

Вычислить интеграл тремя методами: прямоугольников, трапеций и методом парабол (Симпсона), используя автоматический выбор шага интегрирования.

Точность вычислений ε =10^-4.

Таблица заданий № 1.

№ п/п	Уравнение	№ п/п	Уравнение	№ п/п	Уравнение

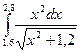
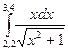
Таблица заданий № 2.

№ п/п	Уравнение	№ п/п	Уравнение	№ п/п	Уравнение

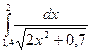
ЛАБОРАТОРНАЯ РАБОТА № 3
«Уточнение корня уравнения»

Дата добавления: 2017-02-01