Результаты работы в Eureka.

РЕЗУЛЬТАТЫ РАБОТЫ В QBASIC

ВИД ПРОГРАММЫ НА ЯЗЫКЕ QBASIC

DECLARE SUB iter (x0!, e!, kol!, root!)

DECLARE SUB iter (x0!, e!, kol!, root!)

DECLARE SUB dix (a!, b!, e!, root!)

DECLARE SUB kas (a!, b!, x!, e!, root!)

DECLARE FUNCTION F! (x!)

DECLARE FUNCTION G! (x!)

DECLARE FUNCTION F1! (x!)

DECLARE FUNCTION F2! (x!)

DECLARE FUNCTION G2! (x!)

REM численное решение не линейных уравнений

'уточнение корня методами касательных/дихот/ньютона/итерации

CLS

PRINT "проверка существования корня"

PRINT " y = = x - 2 + SIN(1 / x)"

REM ввод отрезка с проверкой на сущ решения

DO

INPUT "a= "; a

INPUT "b= "; b

INPUT "точность решения Eps="; e

LOOP WHILE F(a) * F(b) > 0

REM мет дихотомии или метод деления отрезка пополам

CALL dix(a, b, e, root)

PRINT "корень ур по методу дихотомии="; root

PRINT "значение функции F(x)=";

PRINT USING " ##.######"; F(root)

PRINT "-------------------------------------------"

REM метод касательных или метод Ньютона

INPUT "введите начальное значение корня на (a,b) X0="; x

IF F(x) * F2(x) > 0 THEN

PRINT "метод касательных(Ньютона) Применим"

a = 1: b = 3

CALL kas(a, b, x, e, root)

PRINT "корень по методу касательных="; root

PRINT "значение функции F(x)=";

PRINT USING " ##.######"; F(root)

ELSE

PRINT "метод касательных(Ньютона) НЕ Применим"

END IF

PRINT "-------------------------------------------"

REM метод итерации

INPUT "введите XO="; x0

IF ABS(G1(x)) < 1 THEN

PRINT "метод Не применим"

ELSE

a = 1: b = 3

CALL iter(x0, e, kol, root)

PRINT "корень по методу итерации="; root

PRINT "количество итериций k="; kol

PRINT "значение функции F(x)=";

PRINT USING " ##.######"; F(root)

END IF

END

SUB dix (a, b, e, root)

x = (a + b) / 2

DO

IF F(x) * F(a) < 0 THEN

b = x

ELSE

a = x

END IF

x = (b + a) / 2

LOOP UNTIL (b - a) < e

root = (b + a) / 2

END SUB

FUNCTION F (x)

F = x - 2 + SIN(1 / x)

END FUNCTION

FUNCTION F1 (x)

F1 = 2 + COS(1 / x)

END FUNCTION

FUNCTION F2 (x)

F2 = -SIN(1 / x)

END FUNCTION

FUNCTION G (x)

G = 2 - SIN(1 / x)

END FUNCTION

FUNCTION G1 (x)

G1 = -COS(1 / x)

END FUNCTION

SUB iter (x0, e, kol, root)

kol = 0

x = x0

DO

y = F1(x)

kol = kol + 1

x = y

LOOP UNTIL ABS(y - x) < e

root = y

END SUB

SUB kas (a, b, x, e, root)

DO

x = x - F(x) / F1(x)

LOOP UNTIL ABS(F(x) / F1(x)) < e

root = x

END SUB

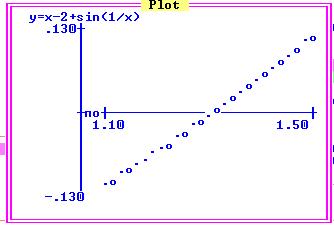
Рекомендации по решению задачи:

1. Решить задачу, используя ППП Eureka.

2. Исходя из полученного решения, выбрать границы существования корня.

3. Составить блок – схему решения и программу на QBasic.

Контрольные вопросы

1. В чем заключается геометрический смысл метода половинного деления?

2. Какой оператор цикла используется в процедуре дихотомии?

3. Какими свойствами должна обладать функция F(x), чтобы методом половинного деления можно было гарантировать решение уравнения F(x)?

4. Что необходимо для нахождения хотя ы одного действительного корня уравнения F(x) методом половинного деления?

5. Какие процедуры функции используются в программе?

6. Какой функцией заменяется левая часть уравнения F(x)=0 в методе итерации?

7. Что называется сходимостью метода итерации?

8. Каково условие сходимости метода итерации и как это условие проверяется в программе?

9. В чем заключается геометрическая интерпретация метода Ньютона?

10. Исходя из чего выбирается в методе Ньютона первое приближение Х₀

11. для чего в программе предусмотрена процедура-функции для второй производной от исходной функции?

Варианты заданий для самостоятельного решения

Задание.

1. Уточнить корень уравнения, используя следующие методы:

- метод половинного деления;

- метод простой итерации;

- метод касательных (Ньютона).

2. Для вариантов заданий, представленных в таблице 4, выбрать точность вычисления.

3. Для вариантов заданий, представленных в таблице 6, вычислить корень с заданной точностью.

4. Для вариантов заданий, представленных в таблице 7,8,9, установить границы существования корня, точность вычисления, установить границы существования корня.

Таблица заданий № 4.

П\П	Вид уравнения	Начальное приближение корня
1.	x – sin 2x – 1 = 0
2.	2x ^ 3 + 4x – 1 = 0	0.1
3.	x ^ 3 + 12x – 2 = 0	0.95
4.	5 – x – 8lnx = 8	4.32
5.	x ^ 3 + x = 1000	9.42
6.	x – sin x = 0.25	1.17
7.	x ^ 3 – 6x ^ 2 + 20 = 0	2.25
8.	5x ^ 3 + 10x ^ 2 + 5x – 1 = 0	0.6
9.	3sin +0.34x-3.8 =0
10.	x – 3 + sin (3.6x) = 0
11.	arcos(x)- = 0
12.	√1- 0.4x ^ 2 – arcsin x = 0
13.	x – 2 + sin x = 0	1.2
14.	1 – x + sin x – ln (1 + x) = 0
15.	x ^ 2 – ln (1 + x) – 3 = 0
16.	x ^ 3 + x ^ 2 – 3 = 0	0.6
17.	x ^ 3 – x – 0.2 = 0	0.9
18.	5x ^ 3 – x – 1 = 0	0.6
19.	x ^ 3 – 2x – 5 = 0	1.9
20.	x ^ 3 + x = 1000	9.1
21.	x ^ 4 + 2x ^ 3 – x – 1 = 0
22.	x ^ 3 – x – 2 = 0	0.9
23.	x – sin x/2 – 1 = 0
24.	2 ^ 3 + 4x – 1 = 0	0.1
25.	x ^ 3 + 12x – 2 = 0	0.95

Таблица заданий № 5

П\П	Вид уравнения	Отрезок
1.	0.25x ^ 3 + x – 1.2502 = 0	0, 2
2.	0.1x ^ 2 – xlnx = 0	1, 2
3.	3x – 4lnx – 5 = 0	2, 4
4.	e ^ x – e ^ -x – 2 = 0	0, 1
5.	e ^ x + lnx – 10x = 0	3, 4
6.	3x – 14 + e ^ x – e ^ -x = 0	1, 3
7.	3ln ^ 2x + 6lnx– 5 = 0	1, 3
8.	2xsinx – cosx = 0	0.4, 1
9.	xtgx – 1\3 = 0	0.2, 1
10.	√ 1 – x - cos√ 1 – x = 0	0, 1

Таблица заданий № 6

№ вар.	Уравнение	Интервал	Точность
1.	x – 1\ (2 + sin2x) = 0	[0; 1]	10 ־³
2.	arcsin(x\3) - √ 1 – (x\3) ^ 2 = 0	[ 1,5; 3]	10 ־³
3.	x - √ 9 –x+ x ^ 2 = 0	[2; 3]	10 ־³
4.	√1 – x ^ 2 - arcsin x = 0	[0; 1]	10 ־³
5.	tgx – (1/3)(tgx)^3 + (1/5)(tg x) ^ 5 – 1/3 = 0	[0; 0,8]	10 ־³
6.	e ^ x – e (- x) – 2 = 0	[0; 1]	10 ־³
7.	cosx – e(-(x ^ 2) / 2) + x – 1 = 0	[0; 2]	10 ־³
8.	sin(x ^ 2) + cos(x ^ 2) – 10x = 0	[0; 1]	10 ־³
9.	3sin√x + 0,35x – 3,8 = 0	[2; 3]	10 ־³
10.	√1 – 0,4 (x ^ 2) – arcsinx = 0	[0; 1]	10 ־³
11.	1/4(x ^ 3) + x – 1,25 = 0	[0; 1]	10 ^-5
12.	x – sin(x + 2) = 0	[0; 1]	10 ^-5
13.	√1 – x - cos√1 – x = 0	[0; 1]	10 ־³
14.	0,1(x ^ 2) – x lnx = 0	[1; 2]	10 ־³
15.	3x – 4 lnx – 5 = 0	[1;4]	10 ־³
16.	e ^ x + lnx – 10 x = 0	[1; 4]	10 ־³
17.	x tgx – 1/3 = 0	[0; 1]	10 ־³
18.	0,25(x ^ 3) + x – 1,25 = 0	[0; 2]	10 ־³
19.	3x – 14 + e ^ x + e (-x) = 0	[1; 3]	10 ־³
20.	2x sinx – cosx = 0	[0,4; 1]	10 ־³
21.	1/(1 + x ^ 2) – x = 0	[1; 2]	10 ־³
22.	.(tg x) ^ 2 – x = 0	[1; 2]	10 ־³
23.	x + ln(х + 0.5) - 0.5 = 0	[0;2]	10 ־³
24.	x ^^3 – х - 0.2 = 0	[1;1,1]	10 ־³
25.	x^ 4 + 2х^ 3 – х – 1 = 0	[0; 1]	10 ־³
26.	x^ 3 – 0.2х^ 2 - 0.2х - 1.2 = 0	[1;1,5]	10 ־³
27.	2sin^2х/3 – Зсоs^2х/4 = 0	[0;П/2]	10־³
28.	x ^ 4 + 0.8х^ 3 - 0.4х ^ 2 - 1.4х - 1.2 = 0	[-1,2;-0,5]	10־³
29.	x ^ 4 - 4.1х ^ 3 + х^ 2 - 5.1х + 4.1 = 0	[3,7;5]	10־³
30.	х2^ х – 1 = 0	[0;1]	10־³

Таблица заданий № 7

№ вар	Уравнение	№ вар	Уравнение
1.	x – sinx = 0,25 16.	16.	tg(0,3x + 0,4) = x ^ 2
2.	tg(0,58x + 0,1) = x ^ 217.	17.	x ^ 2 – 20sinx = 0
3.	√x – cos(0,387x) = 018.	18.	ctgx – x/4 = 0
4.	tg(0,4x + 0,4) = x ^ 2 19.	19.	tg(0,47x + 0,20 = 0
5.	lgx – 7/(2x + 6) = 020.	20.	x ^ 2 + 4sinx = 0
6.	tg(0,5x + 0,2) = x ^ 2 21.	21.	ctgx – x/2 = 0
7.	3x – cosx – 1 = 022.	22.	2x – lgx – 7 = 0
8.	x + lgx = 0,523.	23.	tg(0,44x + 0,30 = 0
9.	tg(0,5x + 0,1) = x ^ 2 24.	24.	3x – cosx – 1 = 0
10.	x ^ 2 + 4sinx = 025.	25.	ctgx – x/10 = 0
11.	ctg1,05x – x ^ 2 = 026.	26.	x ^ 2 + 4sinx = 0
12.	tg(0,4x + 0,3) = x ^ 2 27.	27.	tg(0,36x + 0,4) = 0
13.	xlgx – 1,2 = 028.	28.	x + lgx = 0,5
14.	1,8x ^ 2 – sin10x = 0 29.	29.	ctgx – x/5 = 0
15.	ctgx – x/4 = 030.	30.	2lgx – x/2 + 1 = 0

Таблица заданий № 8

№ вар	Уравнение	№ вар	Уравнение
1.	x ^ 3 – 3x ^ 2 + 9x – 8 = 0.		x ^ 3 + 4x – 6 = 0
2.	x ^ 3 – 6x – 8 = 0		x ^ 3 + 0,2x ^ 2 + 0,5x + 0,8 = 0
3.	x ^ 3 – 3x ^ 2 + 6x + 3 = 0		x ^ 3 – 3x 62 + 12x – 12 = 0
4.	x ^3 – 0,1x ^ 2 + 0,4x –1,5 = 0		x ^3 -0,2 x^2 + 0,3x + 1,2 = 0
5.	x ^ 3 – 3x ^ 2 + 9x + 2= 0		x ^ 3 – 2x + 4 = 0
6.	x ^ 2 + x – 5 = 0		x ^ 3 – 0,2x ^ 2 + 0,5x – 1,4 = 0
7.	x ^ 3+ 0,2 x ^2 +0,5x –1,2 = 0		x ^ 3 – 3x ^ 2 + 6x – 5 = 0
8.	x ^ 3 + 3x + 1 = 0		x ^ 3 – 0,1x ^ 2 + 0,4x + 1,2 = 0
9.	x ^ 3 + 0,2x ^ 2 + 0,5x – 2 = 0		x ^ 3 – 0,2x ^ 2 + 0,5x – 1 = 0
10.	x ^ 3 – 3x ^ 2 + 12x – 9 = 0		x ^ 3 + 3x ^ 2 + 12x + 3 = 0
11.	x ^3 –0,2x ^ 2 + 0,3x – 1,2 = 0		x ^ 3 – 0,1x ^ 2 + 0,4x + 2 = 0
12.	x ^ 3 – 3x ^ 2 + 6x – 2 = 0		x ^ 3 – 0,2 x ^ 2 + 0,4x – 1,4 = 0
13.	x ^ 3 –0,1x ^ 2 +0,4x –1,5 = 0		x ^ 3 + 0,4x ^ 2 + 0,6x – 1,6 = 0
14.	x ^ 3 + 3x ^ 2 + 6x – 1 = 0		x ^3 + x – 3 = 0
15.	x ^ 3 +0,1x ^ 2+0,4x –1,2 = 0		x ^ 3 – 0,2x ^ 2 + 0,5x + 1,4 = 0

Таблица заданий № 9

№ вар	Уравнение	№ вар	Уравнение
1).	2x ^ 3 – 3x ^ 2 – 12x – 5 = 0		2x ^ 3 – 3x ^ 2 – 12x + 1 = 0
2).	x ^ 3 – 3x ^ 2 – 24x – 3 = 0		x ^ 3 – 3x ^ 2 – 24x – 5 = 0
3).	x ^ 3 – 3x ^ 2 + 3 = 0		x ^ 3 – 4x ^ 2 + 2 = 0
4).	x ^ 3 – 12x + 6 = 0		x ^ 3 – 12x – 5 = 0
5).	x ^ 3 + 3x ^ 2 – 24x – 10 = 0		x ^ 3 + 3x ^ 2 – 24x + 1 = 0
6).	2x ^ 3 – 3x ^ 2 – 12x + 10 = 0		2x 6 3 – 3x^ 2 – 12x + 12 = 0
7).	2x ^ 3 + 9x ^ 2 – 21 = 0		2x ^ 3 + 9x ^ 2 – 6 = 0
8).	x ^ 3 – 3x ^ 2 + 2,5 = 0		x ^ 3 – 3x ^ 2 + 1,5 = 0
9).	x ^ 3 + 3x ^ 2 – 2 = 0		x ^ 3 – 3x ^ 2 – 24x + 10 = 0
10).	x ^ 3 + 3x ^ 2 – 3,5 = 0		x ^ 3 + 3x ^ 2 – 24x – 3 = 0
11).	x ^ 3 + 3x ^ 2 – 24x + 10 = 0		x ^ 3 – 12x – 10 = 0
12).	x ^ 3 – 3x ^ 2 – 24x – 8 = 0		2x ^ 3 + 9x ^ 2 – 4 = 0
13).	2x ^ 3 + 9x ^ 2 – 10 = 0		2x ^ 3 – 3x ^ 2 – 12x + 8 = 0
14).	x^ 3 – 12x + 10 = 0		X ^ 3 + 3x ^ 2 – 1 = 0
15).	x ^ 3 +3x ^ 2 – 3 = 0		x ^ 3 – 3x ^ 2 + 3,5 = 0

ЛАБОРАТОРНАЯ РАБОТА № 4
«Методы численного решения дифференциальных уравнений.
Уравнения 1-го порядка»

Цель работы

Ознакомление с принципом модульного программирования на примере задачи решения дифференциальных уравнений и использование оболочки QBasic для построения подпрограмм и головного модуля.

Дата добавления: 2017-02-01