Метод ветвей и границ для задачи целочисленного программирования.

Рассмотрим частично целочисленную задачу ЛП:

минимизировать

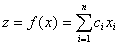(13.23)

при условиях

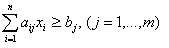; (13.24)

; (13.25)

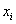- целые числа. (13.26)

Процесс поиска оптимального решения начинают с решения непрерывной задачи ЛП. Если полученный при этом оптимальный план 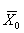не удовлетворяет условию (13.26), то значение целевой функции 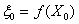дает нижнюю оценку для искомого решения, т.е. .

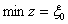Пусть некоторая переменная х_i0 (1≤ i₀ ≤ т) не получила в плане 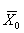целочисленного решения. В целочисленном плане значение х_i0 следует либо уменьшить, по крайней мере до [ х_i0 ], либо увеличить, по крайней мере до [ х_i0 ] + 1.

Если границы изменения х_i0 заранее не заданы, то их можно вычислить, решив для этого две вспомогательные задачи ЛП. Эти задачи состоят в максимизации и минимизации х_i0 при условиях (13.24) и (13,25).

Теперь для каждого фиксированного целочисленного значения х_i0 в найденном отрезке [х_i0min, х_i0max] находят min z, решая задачу ЛП с ограничениями (13.24), (13.25) и с дополнительным ограничением х_i0≤k_i0..

Таким образом, все указанные выше возможности можно представить в виде некоторого дерева, в котором вершина 0 отвечает плану 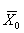, а каждая из соединенных с ней вершин отвечает оптимальному плану следующей задачи: минимизировать z при условиях (13.24), (13.25) и дополнительном условии, что переменной х_i0 дано значение х_i0 ≤ к_i0, где к_io - целое число. Каждой из таких вершин приписывают оценку, которая равна min z при указанных выше ограничениях. Очевидно, 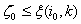, для всех k.

Если оптимальные планы полученных задач удовлетворяют условиям целочисленности, то план с минимальной оценкой 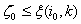и будет оптимальным планом исходной задачи. В противном случае возникает необходимость в продолжении ветвления. При этом каждый раз для очередного ветвления выбирают вершину с наименьшей оценкой.

Любой маршрут в дереве от начальной вершины 0 до некоторой вершины определяет допустимую последовательность выбора целочисленных решений для переменных. Процесс продолжают до тех пор, пока продолжение ветвления становится невозможным.

Каждая конечная вершина отвечает некоторому допустимому целочисленному плану. Вершина с минимальной оценкой дает оптимальный план.

Рассмотрим алгоритм решения задачи целочисленного программирования.

На первом этапе необходимо задать множество G⁽⁰⁾, определяемое условиями (13,24), (13.25).

На втором этапе формируются множества 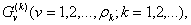задаваемые условиями (13.24), (13.25) и дополнительным условием

x_j≤[x_j0] или x_j≥[ x_j0] +1 (13.27)

где [x_j0]- целая часть х_j0.

На третьем этапе осуществляется вычисление оценок. Для множества G⁽⁰⁾ оценку 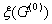определяют как 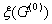=f( 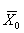), где 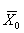- оптимальный план непрерывной задачи ЛП. Для множества 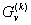оценку 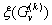определяют аналогично:

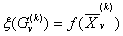
где 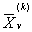-оптимальный план задачи с условиями (13.24), (13.25) и с дополнительным условием (13.27).

Если множество 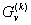оказывается пустым, ему приписывают оценку = ∞.

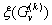На четвертом этапе осуществляется нахождение планов. Если план 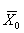удовлетворяет условию целочисленности (13.26), 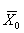-оптимальный план задачи. Если 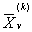удовлетворяет условию целочисленности (13.26), он является оптимальным планом задачи с условиями (13.24), (13.25), (13.27) и некоторым планом исходной задачи (13.23) - (13.26).

На пятом этапе выполняют ветвление. Ветвление производят в том случае, когда план 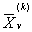не удовлетворяет условию целочисленности (13.26).

Пусть - одна из нецелочисленных компонент плана, где 1 ≤ρ≤n₁, тогда множество 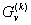разбивают на два подмножества:

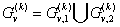
.причем

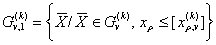; (13.28)

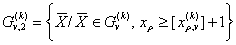(13.29)

Укажем некоторые особенности метода ветвей и границ для задач ЦП.

1. Если все коэффициенты с_j целевой функции - целые при 1 ≤j≤n_i и равны нулю при j > n_i, то оценку 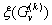МОЖНО заменить на более сильную оценку 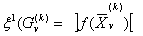, где ]а[ обозначено наименьшее целое, но не меньшее, чем а, т.е. округленное до ближайшего целого с избытком.

2. Алгоритм метода в вычислительном отношении представляет собой последовательность задач ЛП, причем конечность алгоритма следует из предполагаемой ограниченности множества G.

3. Из описания -алгоритма следует, что в применении метода ветвей и границ для полностью целочисленных и для частично.целочисленных задач нет никакой разницы.

Геометрически этот метод можно интерпретировать таким образом. Гиперплоскость, определяемая функцией задачи, вдавливается внутрь многогранника планов соответствующей задачи ЛП до встречи с ближайшей целочисленной точкой этого многогранника.

■ Пример 1 применения метода ветвей и границ для решения задач дискретного программирования.

Возьмем задачу

Максимизировать 3 x₁ +3 x₂ +13 x₃ (13.30)

При ограничениях -3 x₁+6 x₂+7 x₃≤8; (13.31)

6 x₁-3 x₂ +7 x₃≤8; (13.32)

где каждая переменная x_j должнабыть неотрицательным целым. Предположим, что заданы границы на каждую переменную:

0≤ x_j≤5, j=1,2,3.

Как принято, обозначим x₀^t значение целевой функции.

На итерации 1 примем нижнюю границу x ₀¹ , поскольку при всех x_j =0 имеем допустимое решение. Основой список содержит лишь одну задачу линейного программирования (13.30) (13.31) и (13.32), которую назовем задачей 1. Выберем эту задачу на шаге 1 и найдем ее оптимальное решение на шаге 2:

x₀=16, x₁=x₂= 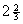, x₃=0.

Поскольку решение не является целочисленным, перейдем от шага 3 к шагу 4 и выберем x₁. Внесем далее в основной список

Задачу 2: ограничения (13.33)

3≤x₁≤5; 0≤x₂≤5; 0≤x₃≤5;

Задачу 3: ограничения (13.34)

0≤x₁≤2; 0≤x₂≤5; 0≤x₃≤5;

Допустимое решение задачи 2 отсутствует. Поэтому выберем x₀²= x₀³=0 и вернемся к шагу 1. выберем теперь задачу 3 и получим на шаге 2 оптимальное решение

x₀= 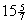, x₁=x₂=2, x₃= 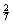, не являющееся целочисленным. Дальнейший ход решения задачи показан на рис. 13.1.

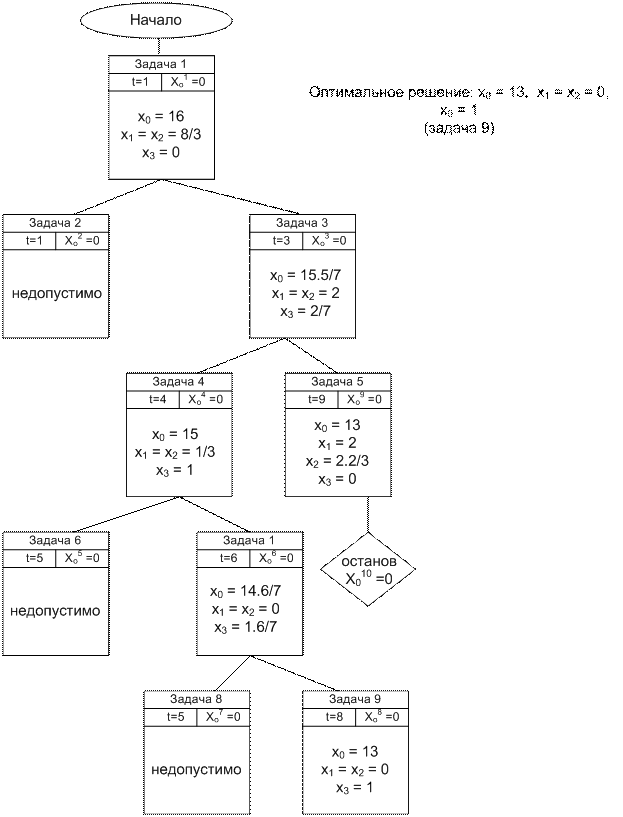
Рис. 13.1

Решением задачи является оптимальный план x ₁= x ₂=0, x ₃=1, значение целевой функции f (x)=13.

Дата добавления: 2017-02-01