Лекция 14. Нелинейное программирование.

13.1. Нелинейное программирование - раздел теории оптимизации (теории экстремальных задач), посвященный исследованию и решению задач минимизации (максимизации), в которых целевая функция и ограничения не являются линейными. К нелинейному программированию относят квадратичное, дробное, выпуклое, дискретное, целочисленное и геометрическое программирование.

В общем виде задачу нелинейного программирования можно сформулировать так:

F (х) → min (max) (1)

при условии

g(x) ≤ 0, (2)

где х - вектор искомых переменных; F (х) - целевая числовая функция; g(x) - вектор-функция системы ограничений.

При этом могут быть разные случаи: целевая функция - нелинейная, а ограничения - линейны; целевая функция - линейная, а ограничения (хотя бы одно из них) - нелинейные; целевая функция и ограничения нелинейные. Задачи условной оптимизации нелинейного программирования бывают двух типов: когда в ограничениях (2) имеют место а) знаки равенства б) знаки неравенства.

Решение задачи нелинейного программирования (поиск глобального минимума или максимума) состоит в отыскании таких значений переменных, подчиненных системе ограничений, при которых достигает минимума или максимума данная целевая функция.

При решении некоторых нелинейных задач иногда удается использовать линейную теорию. Для этого вводят допущение, что на том или ином участке целевая функция возрастает или убывает пропорционально изменению переменных. Такой подход называется методом кусочно-линейных приближений.

Нелинейные задачи с ограничениями в форме равенств нередко решаются с помощью введения функции Лагранжа.

Функция Лагранжа для функции имеет вид:

,

где - вектор множителей Лагранжа.

Среди большого числа вычислительных алгоритмов нелинейного программирования значительное место занимают различные варианты градиентных методов (метод проекции градиента, метод условного градиента и т. п.), методы штрафных функций, методы барьерных функций, метод модифицированных функций Лагранжа и др.

Универсального метода, позволяющего находить наиболее эффективным способом решение любой нелинейной задачи, не существует. Поэтому для каждой конкретной задачи, учитывая ее специфику, подбирают тот или иной наиболее подходящий метод (и алгоритм) решения.

Постановки задач нелинейного программирования. Задачи нелинейного программирования на практике возникают довольно часто, например, когда затраты растут непропорционально количеству закупленных или произведенных товаров. Хорошо известно, что чем больше партия закупаемого товара, тем меньше стоимость единицы продукта. Любому покупателю знакомо понятие розничных и оптовых цен. Рассмотрим конкретный пример, иллюстрирующий данную ситуацию.

Планирование производства продукции. На действующем предприятии планируется организовать выпуск новых видов продукции. Для организации производства необходимо приобретать сырье, стоимость которого колеблется в зависимости от спроса. Цены на готовую продукцию предприятия предполагаются стабильными.

Итак, необходимо провести исследования о производстве двух видов изделий, для которых планируется приобретение сырья, цена которого зависит от объема закупаемой партии и спроса на рынке на сырье данного типа. Цены же на продукцию предприятия утверждены с учетом реальной обстановки и должны сохраняться неизменными. Объемы производства предстоит определить исходя из анализа сырьевой проблемы и ограниченности производственных ресурсов.

Пусть х ₁, х ₂ - объемы производимой продукции 1-го и 2-го видов, с ₁, с₂ - цена единицы продукции 1-го и 2-го видов соответственно. Затраты на приобретение и доставку сырья представляют собой нелинейную функцию, зависящую от объема закупаемого товара, f ₁(x ₁), f ₂(x ₂). Таким образом, экономическая рентабельность планируемых мероприятий оценивается формулой

(3)

Предприятие для производства новых видов продукции может выделить лишь часть своих мощностей, что накладывает дополнительные ограничения на максимальный объем выпуска новых видов изделий. Устанавливаются также лимиты на стоимость основных фондов (эксплуатация зданий, снабжение электроэнергией, амортизационные отчисления) в объеме b ₁, и стоимость производственных процессов (вспомогательные материалы, заработная плата, накладные расходы и др.) в объеме b ₂ Известно, что изготовление единицы продукции первого вида требует а ₁₁ затрат из основных фондов и а ₁₂трудовых затрат, а единицы продукции второго вида затрат в размере а ₂₁ и а ₂₂ соответственно. Учет этих факторов приводит к условиям

(4)

Теперь можно сформулировать задачу: определить такие х₁, х₂, которые бы обеспечивали максимум функционала

(5)

при ограничениях

(6)

x₁ ,x₂≤0.

Таким образом сформулирована задача, в которой целевая функция является нелинейной.

Квадратичное программирование - раздел нелинейного программирования, включающий совокупность методов решения экстремальных задач, в которых целевая функция представляет собой многочлен второй степени, а ограничения - линейные функции.

Задача квадратичного программирования может быть записана в матричной форме следующим образом:

(7)

где х - n -мерный вектор-столбец; х ' - n -мерная вектор-строка; с' - n -мерная вектор-строка; b - m -мерный вектор-столбец; А - матрица размера т × п; D - симметрическая квадратная матрица порядка n;

(8)

Решить задачу квадратичного программирования это значит найти точку 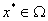, для которой достигается максимум функции

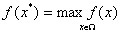, (9)

где Ώ - множество допустимых планов задачи, определяемое системой ограничений

Ах = b, х > 0. (10)

Если D = 0, то задача сводится к задаче линейного программирования. Если целевая функция задачи квадратичного программирования ограничена сверху, то задача обязательно имеет оптимальное решение, т.е. точку глобального максимума.

Для нахождения глобального максимума общей задачи (1) не существует эффективных вычислительных методов.

В настоящее время развиты методы выпуклого квадратичного программирования - раздела выпуклого программирования, который занимается задачами поиска глобального максимума выпуклой квадратичной функции на многогранном множестве. В этом классе задач доказано, что если матрица D является отрицательно определенной, то целевая функция (7) будет ограничена сверху, и задача (7) будет иметь оптимальное решение, и притом единственное (при условии, что допустимое множество непусто).

Важное место в выпуклом квадратичном программировании занимает двойственная задача.

В соответствии с общим принципом двойственности для задачи (7) двойственная задача имеет вид:

(11)

при условиях

, (12)

где A’ - матрица, транспонированная по отношению к А; с - n -мерный вектор-столбец; λ - m -мерный вектор-столбец.

В линейном случае (при D = 0) определение двойственной задачи (11) - (12) совпадает с принятым в линейном программировании.

Как и в случае линейного программирования в квадратичном программировании имеет место теорема двойственности:

если одна из задач двойственной пары разрешима, то и другая задача также разрешима; причем экстремальные значения обеих задач равны.

Условие Куна-Такера для выпуклой задачи (7) - (8) имеет вид:

Ах = b;

; (13)

.

Таким образом, для того чтобы вектор х° был решением задачи (7) - (8), необходимо и достаточно существование вектора v° ≥ 0 и вектора λ ⁰ таких, чтобы система векторов х°, v°, λ ⁰ удовлетворяла условию (13). Любой (2 n + m)-мерный вектор { х, v, λ. }, который является решением системы (13) при условии х ≥0, v ≥0, будет крайней точкой многогранного множества, т.е. базисным решением системы:

Ах = b;

(14)

С учетом этого условия решение задачи квадратичного программирования сводится к нахождению базисных решений многогранных множеств, что может быть успешно осуществлено симплекс-методом линейного программирования за конечное число шагов.

Кроме общих методов выпуклого программирования специально для задачи выпуклого квадратичного программирования разработано большое количество численных методов, и в том числе конечных. Наиболее употребительными конечными методами являются: симплексный метод Билла, метод сопряженных градиентов, симплексный метод Вулфа. Эффективность того или иного метода существенно зависит от специфики решаемой задачи.

Рассмотрим пример решения задачи нелинейного программирования с ограничениями в виде неравенств. Пусть требуется минимизировать функцию

f (x) =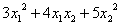

при ограничениях х₁ > 0; х₂ > 0; х₁ + х₂ ≥ 4. Перепишем условие задачи следующим образом:

,

Преобразуем ограничения, добавив в левую часть ослабляющие переменные и изменив знак на равенство:

Далее запишем функцию Лагранжа

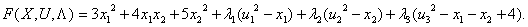. Необходимые условия минимума для данной функции:

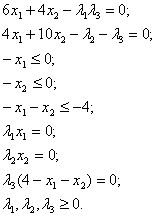
Принимая во внимание три последних равенства, можно сделать вывод о том, что либо множители Лагранжа, либо искомые переменные должны быть равны нулю. При этом хотя бы один из множителей Лагранжа должен быть отличен от нуля. Положим

λ₁= λ2=0, тогда (поскольку решается задача минимизации) должно выполняться неравенство λ₃ > 0, откуда следует 4 – x₁ - х₂ = 0 или 4 – х₁= х₂. Подставляем данное выражение для параметра х₂ в два первых равенства и решаем их:

Приводя подобные члены, получим

. Перенесем множитель Лагранжа в правую часть:

Решая данную систему, получим

.

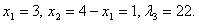Нетрудно проверить, что эти решения являются условиями минимума и функция имеет минимальное значение, равное 44 в точке с координатами (3, 1).

Дата добавления: 2017-02-01