Лекция 15. Динамическое программирование

Решение задач нелинейного программирования в системе MATLAB

Для решения задач квадратичного программирования предназначена функция quadprog. Интерфейс quadprog практически не отличается от linprog, за исключением того, что первыми двумя входными параметрами являются массив H и вектор-столбец f, соответствующие матрице Н и вектору f целевой функции. Вместо матриц и векторов отсутствующих ограничений задаются пустые массивы.

Динамическое программирование - раздел теории оптимизации, посвященный исследованию и решению экстремальных задач специального вида, в которых целевая функция (целевой функционал) имеет вид суммы слагаемых (соответственно - интеграла). В основе метода динамического программирования лежит идея разбиения исходной задачи на последовательный ряд более простых задач. Основной областью приложения динамического программирования являются многошаговые процессы, т.е. процессы, протекающие во времени (дискретном или непрерывном).

Главным рабочим инструментом динамического программирования является метод рекуррентных соотношений, в основе которого лежит необходимое условие оптимальности, выражаемое обычно в виде так называемого принципа оптимальности и уравнения Беллмана (по имени американского математика Р. Беллмана).

Принцип оптимальности Беллмана утверждает, что оптимальный процесс (т.е. оптимальное управление и соответствующая ему оптимальная траектория) для всего периода управления обладает тем свойством, что любая его часть, рассматриваемая на промежутке времени, входящем в исходный промежуток, также представляет собой оптимальный процесс для этого частичного промежутка времени. Иными словами, любая часть опти­мального процесса необходимо является оптимальным процессом.

Основные особенности дискретной модели динамического программирования состоят в следующем:

1) задача оптимизации интерпретируется как многошаговый процесс управления;

2) целевая функция равна сумме целевых функций для каждого шага;

3) выбор управлений х_к на к-м шаге определяется только состоянием системы S_K-1 на
предыдущем шаге и не зависит от состояния системы на более ранних этапах управления;

4) состояние S_k на к-м шаге зависит только от предшествующего состояния S_k-1, и управления x_k, принимаемого на данном шаге, т.е.

S_k=f_k(S_k-1, x_k) (1)

Схематически модель динамического программирования иллюстрирует следующая схема:

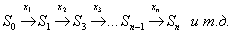(2)

Число этапов n, как правило, считается фиксированным, однако в некоторых задачах n может быть неограниченным, что соответствует задаче с бесконечным горизонтом управления.

Следует иметь в виду, что принцип Беллмана справедлив только для задач, для которых целевые функции можно описать в виде аддитивных функций от траектории, т. е. для процессов с определенной структурой зависимости управлений.

Это означает, что критерий оптимальности (целевая функция) F имеет вид

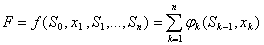, (3)

где числовая функция φ_k оценивает качество управленческого решения на к-м шаге.

Оптимальное управление удовлетворяет следующему принципу оптимальности Беллмана: предположим, что, осуществляя управление, уже выбрана последовательность оптимальных управлений x ₁, x₂,..., x_p, на первых р шагах, которой соответствует последовательность состояний (т.е. траектория) S₁, S₂,..., S_p. Требуется завершить процесс, т.е. выбрать x_p+1.,..., х_n (а значит и S_p+1,,..., S_n). Тогда, если завершающая часть процесса не будет максимизировать функцию

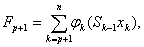(4)

то и весь процесс управления не будет оптимальным. В частности, при р = п - 1 получа­ем требование максимизации функции , зависящей от переменной х_n.

На основе принципа оптимальности Беллмана строится система рекуррентных соотношений (уравнения Беллмана):

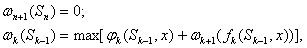(5)

где /, - заданная векторная функция соответствующих переменных, к = п,n-1,...,1, которым должен удовлетворять оптимальный процесс.

Максимум в правой части равенства (2) берется по всем управлениям х, допустимым на шаге к. Тем самым, при вычислении на каждом шаге приходится решать семейство задач максимизации функции переменной х, зависящих от состояния S_k-1 на предыдущем (k -1)-м шаге. При этом величина 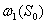есть оптимальное значение критерия оптимальности.

Вычисление оптимального процесса на основе уравнений Беллмана (2) в каждом конкретном случае может оказаться непростой задачей, требующей навыка и изобретательности.

Модели динамического программирования применяются при распределении дефицитных капитальных вложений между предприятиями, при составлении календарных планов текущего и капитального ремонта оборудования и его замены и т.д.

Дата добавления: 2017-02-01